
- •1. Элементы выпуклого анализа.
- •2. Осн. З. Выпуклого программирования. Седловая точка и оптимал. План.
- •3. Теорема Куна-Таккера.
- •4. Критерий оптимальности для гладкой выпуклой задачи.
- •5. Теория двойственности в выпуклом программировании
- •6. Решение одной задачи квадратичного программирования.
- •7. О существовании решения.
- •8. Задача на безусловный минимум.
- •9. Задача с равенствами. Метод исключения.
- •10. Задача с равенствами. Обобщенное правило Лагранжа
- •11. Задача с равенствами. Классическое правило Лагранжа.
- •12. Задача с равенствами. Лемма о включении.
- •13. Задача с равенствами. Необходимое условие 1 порядка.
- •14. Задача с равенствами. Другое доказательство принципа Лагранжа.
- •15. Задача с равенствами. Случай линейных ограничений.
- •16.Задача с равенствами. Условия 2 порядка.
- •17. Задача с неравенствами. Условие 1 порядка.
- •18. Задача с неравенствами. Обобщенное правило Лагранжа.
- •19. Задача с неравенствами. Классическое правило Лагранжа.
- •20. Задача с неравенствами. Условия 2 порядка.
- •21. Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
- •22. Векторная оптимизация. Принципы выбора.
9. Задача с равенствами. Метод исключения.
![]() (1).Будем
предполагать, что ф-ции
и
(1).Будем
предполагать, что ф-ции
и
![]() имеют нужную гладкость.
имеют нужную гладкость.
В некоторых случаях
из системы ограничений задачи (1),
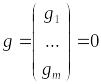 (2)
(2)
удается выразить
(исключить) некоторые
![]() переменных через остальные
переменных через остальные
![]() .
Не ограничивая общности, будем считать,
что первые
переменных выражены через последние
.
Не ограничивая общности, будем считать,
что первые
переменных выражены через последние
![]() (переменные можно просто перенумеровать),
то есть система (2) эквивалентна системе
(переменные можно просто перенумеровать),
то есть система (2) эквивалентна системе
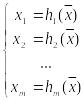 ,
(3)
где
,
(3)
где
![]() – некоторые
функции,
– некоторые
функции,
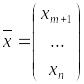 .
.
Система (3) наз.
уравнениями
связи.
Исключая с помощью (3), первые переменные
из функции
,
приходим к задаче
![]() ,
(4)
,
(4)
где
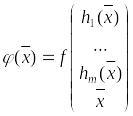 .
.
Задачи (1) и (4)
эквивалентны в том смысле, что если
–
оптимальный план задачи (1), то его
последние компоненты
![]() – оптимальный план задачи (4), обратно,
если
– оптимальный план задачи (4), то вектор
– оптимальный план задачи (4), обратно,
если
– оптимальный план задачи (4), то вектор
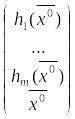 – оптимальный план задачи (1).
– оптимальный план задачи (1).
Задача (4) – задача на безусловный минимум. Метод исключения, описанный выше, значительно упрощает задачу. Его применяют и в тех случаях, когда лишь из части уравнений системы (2) можно выделить некоторые переменные через остальные. Тогда, исключая эти переменные из целевой функции и остальных ограничений (в которых не удается выразить переменные), мы снова приходим к задаче (1), эквивалентной исходной, но с меньшим числом переменных и с меньшим числом ограничений равенств (на количество исключенных переменных).
10. Задача с равенствами. Обобщенное правило Лагранжа
(1).Будем предполагать, что ф-ции и имеют нужную гладкость. По параметрам задачи (1) составим обобщенную ф-цию Лагранжа:
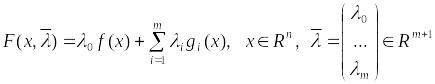 - множитель
Лагранжа
функции.
Для получения условия оптимальности
будем использовать теорему о неявных
функциях (
- множитель
Лагранжа
функции.
Для получения условия оптимальности
будем использовать теорему о неявных
функциях (![]() ).
).
Теорема 1
(Обобщённое
правило множителей Лагранжа).
Если
![]() – локально-оптимал. план зад.(1), то
найдётся такой обобщённый вектор
Лагранжа
– локально-оптимал. план зад.(1), то
найдётся такой обобщённый вектор
Лагранжа
![]() ,
что
,
что
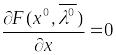 (5)
(5)
Доказательство. Распишем условие (5), получаем:
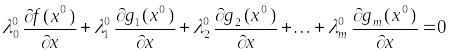 (5*).
Тогда
требование теор. означает на самом деле,
что если
– локально-оптимал. план, то вектора
(5*).
Тогда
требование теор. означает на самом деле,
что если
– локально-оптимал. план, то вектора
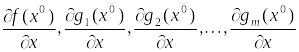 (6)
явл. лин.
зависимыми.
(6)
явл. лин.
зависимыми.
Предположим
противное. Требование теор. не выполн.,
несмотря на то, что
– локально-оптимал. план, т.е. вектора(6)
лин. независ-е. Рассм. тогда вектор-ф-цию
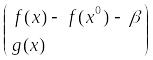 переменных
переменных
![]() и
и
![]() в окрестности точки
в окрестности точки
![]() ,
,
![]() .
Ясно, что если подставить эту точку в
вектор-ф-цию, то она примет нулевое
значение. В силу линейной независимости
векторов (6) в окрестности этой точки
выполняются все условия о неявных
функциях. Согласно теореме найдутся
такие числа
.
Ясно, что если подставить эту точку в
вектор-ф-цию, то она примет нулевое
значение. В силу линейной независимости
векторов (6) в окрестности этой точки
выполняются все условия о неявных
функциях. Согласно теореме найдутся
такие числа
![]() и функция
и функция
![]() ,
что будут выполняться условия:
,
что будут выполняться условия:
1.
![]() 2.
2.
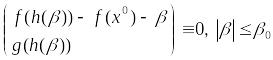 3.
3.
![]() .
.
Тогда условие
![]() означает, что
означает, что
![]() является планами задачи. Поскольку
,
то при достаточно малых
эти планы лежат в сколь угодно малой
окрестности плана
.
Тогда из тождества
является планами задачи. Поскольку
,
то при достаточно малых
эти планы лежат в сколь угодно малой
окрестности плана
.
Тогда из тождества
![]() или
или
![]() при малых отрицательных
при малых отрицательных
![]() получаем
получаем
![]() .
.
Это неравенство означает, что в сколь угодно малой окрестности плана найдутся планы лучшие, чем . Это противоречит локальной оптимизации .
Ч.т.д.
11. Задача с равенствами. Классическое правило Лагранжа.
(1).Будем предполагать, что ф-ции и имеют нужную гладкость.
По параметрам задачи (1) составим классическую ф-цию Лагранжа:
![]() - множитель
Лагранжа
функции.
Для получения условия оптимальности
будем использовать теорему о неявных
функциях (
).
- множитель
Лагранжа
функции.
Для получения условия оптимальности
будем использовать теорему о неявных
функциях (
).
Пусть дана задача:
![]() (1)
(1)
Опр. Некоторый
план зад.(1)
(здесь необязательно оптимал.) будем
называть обыкновенным,
если вектора
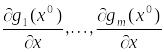 (7) лин.
независимы
(7) лин.
независимы
![]() .
.
Теор.2 (Классич.
правило множителей Лагранжа). Если
– обыкновенный локально-оптимал. план
зад.(1), то всегда найдётся такой единств.
классический вектор Лагранжа
![]() ,
что выполняется условие:
,
что выполняется условие:
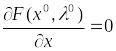 (8)
(8)
Док-тво. Пусть
–обыкновенный
локально-оптимал. план. Док-м, что в силу
обыкновенности в (5*) множитель
![]() .
Предположим противное, т.е.
.
Предположим противное, т.е.
![]() .
Тогда из условия(5*) получаем
.
Тогда из условия(5*) получаем
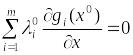 ,
(9) в
котором не все множители
,
(9) в
котором не все множители
![]() нулевые. Тогда(9) означает лин. зависимость
векторов
и противоречит обыкновенности
.
Итак,
.
Разделим тогда выражение (5*) на
нулевые. Тогда(9) означает лин. зависимость
векторов
и противоречит обыкновенности
.
Итак,
.
Разделим тогда выражение (5*) на
![]() и переобозначим:
и переобозначим:
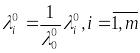 ,
тогда придём к условию (8).
,
тогда придём к условию (8).
Докажем единственность
.
Предположим противное. Найдётся ещё
один вектор Лагранжа
![]() такой, что
такой, что
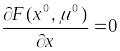 .
Вычитая из этого равенства равенство
(8), придём к
.
Вычитая из этого равенства равенство
(8), придём к
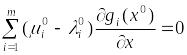 ,
причём не все коэффициенты
,
причём не все коэффициенты
![]() .
Это означает линейную зависимость
векторов (7) и снова противоречит
обыкновенности
.
.
Это означает линейную зависимость
векторов (7) и снова противоречит
обыкновенности
.
Ч.т.д.
