15. Задача с равенствами. Случай линейных ограничений.

Рассмотрим задачу оптимизации: (19)

Эта задача (1), у которой .

Теорема. Пусть − локально-оптимальный план задачи (19). Тогда для любого вектора такого, что (20) выполняется неравенство

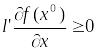(21)

Доказательство. Пусть − локально-оптимальный план и пусть удовлетворяет равенству (20). Построим векторы . Докажем, что они являются планами задачи (19). Действительно, . Ясно, что лежат в сколь угодно малой окрестности при малых .

Допустим противное. Существует направление , подходящее для задачи на плане , то есть этот вектор будет удовлетворять (17), то есть .

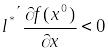По и , согласно лемме о включении найдутся такие планы , лежащие в окрестности точки , что .

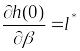Рассмотрим разложение

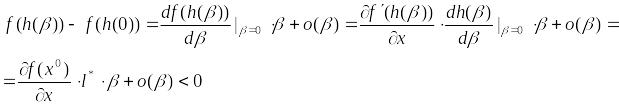
для некоторых малых , то есть получили неравенство . Это неравенство противоречит локальной оптимальности , то есть в любой малой окрестности точки найдутся планы лучшие, чем .

Ч.т.д.

Следствие. Применяя к (20), (21) теорему Фаркаша о неравенстве вследствие равенств, приходим к выводу, что для задачи (19) всегда справедливо классическое правило множителей Лагранжа (не требуется проверки на обыкновенность).

16.Задача с равенствами. Условия 2 порядка.

Пусть дана задача: (1)

Теорема 1 (Необходимое условие оптимальности второго порядка). Пусть − обыкновенный локально-оптимальный план задачи (1) и пусть соответствующий ему вектор Лагранжа. Тогда для любого вектора допустимого по ограничениям 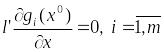выполняется неравенство .

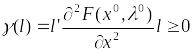Теорема 2 (Достаточное условие оптимальности). Пусть пара − условно-стационарная точка задачи (1). Тогда, если для любого вектора удовлетворяющего условию и выполняется условие , то − локально-оптимальный план задачи (1).

Замечание 1. Если вместо задачи (1) рассмотреть задачу , то и в этом случае условия оптимальности второго порядка будут выполняться, но в силу линейности ограничений здесь не требуется обыкновенности .

Замечание 2. Условие оптимальности второго порядка носит конструктивный характер. Его можно применять при практическом решении задачи (1). Пусть мы нашли условно-стационарную точку. Строим задачу квадратичного программирования.

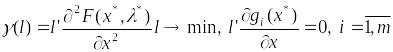(23)

Пусть оптимальный план. Возможны 3 случая:

1. Если 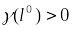, то по достаточному условию оптимальности 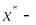локально-оптимальный план.

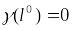2. Если , то для выполняется необходимое условие оптимальности второго порядка, но не выполняется достаточное условие оптимальности. Тем не менее, остаётся подозрительной на решение задачи (1).

3. Если , то в этом случае нужно исключить из дальнейшего рассмотрения как заведомо неоптимальный план (не удовлетворяет необходимому условию оптимальности).

17. Задача с неравенствами. Условие 1 порядка.

Пусть дана задача: (1)

Определение. Пусть – некоторый план, то есть . Говорят, что ое ограничение задачи (1) активно на этом плане, если оно принимает вид и пассивно, если .

Обозн. . Ясно, что если – внутр.точка, то .

Теор.1.Пусть –локально-оптимал. план зад(1).Тогда несовместна с-ма нерав-в:

(2)

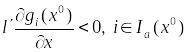(3)

Доказательство. Пусть – локально-оптимальный план задачи (1). Предположим противное, то есть найдётся такой вектор , который удовлетворяет системе (2)-(3). Построим вектор . Докажем, что является планом задачи (1). Действительно, если , то получаем

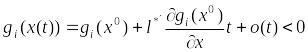при достаточно малых положительных .

Если , то 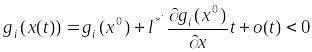при достаточно малых положительных .

Итак, при достаточно малых положительных – планы и они лежат в сколь угодно малой окрестности . Тогда получаем разложение:

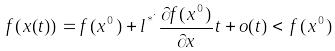
неравенство противоречит локальной оптимальности .

Противоречие доказывает теорему.

Ч.т.д.

Следствие. Пусть – локально-оптимальный план задачи (1), причём – внутренняя точка. Тогда и в этом случае, лишь неравенство несовместно ни для какого вектора . Тогда, очевидно, необходимым условием оптимальности будет условие .
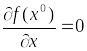