
- •1. Элементы выпуклого анализа.
- •2. Осн. З. Выпуклого программирования. Седловая точка и оптимал. План.
- •3. Теорема Куна-Таккера.
- •4. Критерий оптимальности для гладкой выпуклой задачи.
- •5. Теория двойственности в выпуклом программировании
- •6. Решение одной задачи квадратичного программирования.
- •7. О существовании решения.
- •8. Задача на безусловный минимум.
- •9. Задача с равенствами. Метод исключения.
- •10. Задача с равенствами. Обобщенное правило Лагранжа
- •11. Задача с равенствами. Классическое правило Лагранжа.
- •12. Задача с равенствами. Лемма о включении.
- •13. Задача с равенствами. Необходимое условие 1 порядка.
- •14. Задача с равенствами. Другое доказательство принципа Лагранжа.
- •15. Задача с равенствами. Случай линейных ограничений.
- •16.Задача с равенствами. Условия 2 порядка.
- •17. Задача с неравенствами. Условие 1 порядка.
- •18. Задача с неравенствами. Обобщенное правило Лагранжа.
- •19. Задача с неравенствами. Классическое правило Лагранжа.
- •20. Задача с неравенствами. Условия 2 порядка.
- •21. Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
- •22. Векторная оптимизация. Принципы выбора.
5. Теория двойственности в выпуклом программировании
Рассм. зад.
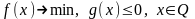 (1). Будем предполагать, что мн-во планов
этой задачи регулярно. Тогда для нее
справедлива теорема Куна-Таккера. По
параметрам зад. (1) составим функцию
Лагранжа, и будем строить две функции.
(1). Будем предполагать, что мн-во планов
этой задачи регулярно. Тогда для нее
справедлива теорема Куна-Таккера. По
параметрам зад. (1) составим функцию
Лагранжа, и будем строить две функции.
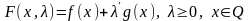
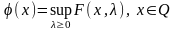 (2),
(2),
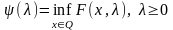 (3)
(3)
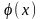 наз. прямой,
наз. прямой,
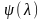 –
двойственной
для задачи (1). Рассмотрим две задачи:
–
двойственной
для задачи (1). Рассмотрим две задачи:
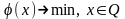 (4),
(4),
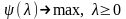 (5)
(5)
Задачу (4) называют
прямой,
а (5) – двойственной
для задачи (1). Множество
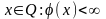 называется множеством
прямых планов,
а множество
называется множеством
прямых планов,
а множество
 – множеством
двойственных планов.
– множеством
двойственных планов.
Рассм. множество
прямых планов. По определению функции
получаем:
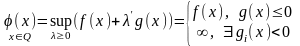 .
Тогда видно, что множество прямых планов
(4) в точности совпадает с множеством
планов основной задачи выпуклого
программирования и на этом множестве
.
Тогда видно, что множество прямых планов
(4) в точности совпадает с множеством
планов основной задачи выпуклого
программирования и на этом множестве
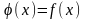 .
Это означает, что задачи (4) и (1) идентичны
(одинаковы).
.
Это означает, что задачи (4) и (1) идентичны
(одинаковы).
Замечание. Если в качестве выпуклой задачи рассмотреть каноническую задачу лин. программирования и построить для нее функцию Лагранжа, а затем пару из прямой и двойственной задач, то нетрудно убедиться, что они в точности совпадают с парой взаимодвойственных задач линейного программирования.
Теорема. (Соотношения двойственности)
Справедливо неравенство
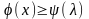 ,
,
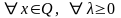 .
(6)
.
(6)Если
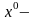 оптимал. план зад.(3), то тогда
оптимал. план зад.(3), то тогда
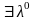 – оптимал. план зад. (4), причем
– оптимал. план зад. (4), причем
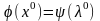 .
(7)
.
(7)
Если
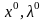 –
оптимал. планы задач(4),(5),то на них
выполн-ся усл.
.
–
оптимал. планы задач(4),(5),то на них
выполн-ся усл.
.4.1) Если на некоторой последовательности двойственных планов
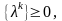
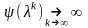 ,
то
,
то
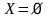 .
.
Если на некоторой последовательности
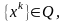
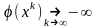 ,
то множество двойственных планов
пусто.
,
то множество двойственных планов
пусто.
Для того чтобы были оптимал. планами(4),(5) необход. и достаточно, чтобы пара была седловой точкой функции Лагранжа для задачи (1).
Если для некоторых планов выполняется , то они являются оптимальными планами (4), (5).
6. Решение одной задачи квадратичного программирования.
Рассмотрим следующую задачу оптимизации
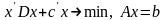 .
(28)
.
(28)
В (28)
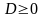 –
симметричная
–
симметричная
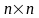 матрица,
матрица,
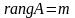 .
.
Очевидно, что (28)
– задача со строго выпуклыми функциями
и линейными ограничениями и имеет форму
основной задачи выпуклого программирования
с равенствами. Для этой задачи справедлива
теорема Куна-Таккера, причем
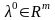 .
Построим для задачи (28) функцию Лагранжа.
.
Построим для задачи (28) функцию Лагранжа.
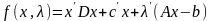 и будем строить
двойственную функцию:
и будем строить
двойственную функцию:
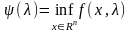 .
Поскольку функция Лагранжа
.
Поскольку функция Лагранжа
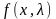 при
при
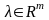 строго
выпукла, то
строго
выпукла, то
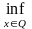 достигается в стационарной точке, то
есть там, где
достигается в стационарной точке, то
есть там, где 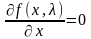 (29)
(29)
Составим условие
стационарности:
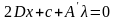
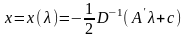 (30)
(30)
Отсюда получаем:
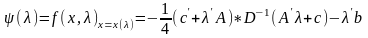 .
И построим двойственную задачу:
.
И построим двойственную задачу:
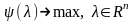 (31)
(31)
Нетрудно убедиться,
что функция
является строго вогнутой относительно
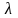 (для этого нужно взять вторую производную
по
от
и убедиться в том, что это будет матрица
отрицательная). И поэтому задача (31)
всегда имеет оптимальный план, и он
достигается в стационарной точке
(для этого нужно взять вторую производную
по
от
и убедиться в том, что это будет матрица
отрицательная). И поэтому задача (31)
всегда имеет оптимальный план, и он
достигается в стационарной точке
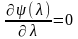 (32)
(32)
Составляем условие стационарности (32)
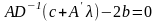 .
.
Отсюда находим оптимальный план (31), получаем:
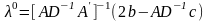 –
оптимальный план
(31).
–
оптимальный план
(31).
По теории двойственности тогда существует оптимальный план и прямой задачи, которая совпадает с (28) и он имеет вид:
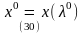
Таким образом, теория двойственности позволяет для задачи (28) сразу получить оптимальный план в явной форме. Задача (28)относится к задачам квадратичного программирования, то есть к задачам с квадратичной целевой функцией и линейными ограничениями.
