
- •1. Элементы выпуклого анализа.
- •2. Осн. З. Выпуклого программирования. Седловая точка и оптимал. План.
- •3. Теорема Куна-Таккера.
- •4. Критерий оптимальности для гладкой выпуклой задачи.
- •5. Теория двойственности в выпуклом программировании
- •6. Решение одной задачи квадратичного программирования.
- •7. О существовании решения.
- •8. Задача на безусловный минимум.
- •9. Задача с равенствами. Метод исключения.
- •10. Задача с равенствами. Обобщенное правило Лагранжа
- •11. Задача с равенствами. Классическое правило Лагранжа.
- •12. Задача с равенствами. Лемма о включении.
- •13. Задача с равенствами. Необходимое условие 1 порядка.
- •14. Задача с равенствами. Другое доказательство принципа Лагранжа.
- •15. Задача с равенствами. Случай линейных ограничений.
- •16.Задача с равенствами. Условия 2 порядка.
- •17. Задача с неравенствами. Условие 1 порядка.
- •18. Задача с неравенствами. Обобщенное правило Лагранжа.
- •19. Задача с неравенствами. Классическое правило Лагранжа.
- •20. Задача с неравенствами. Условия 2 порядка.
- •21. Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
- •22. Векторная оптимизация. Принципы выбора.
3. Теорема Куна-Таккера.
Рассмотрим задачу
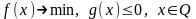 (1), в
которой
– вектор-функция,
ф-ции
– выпуклые ф-ции;
–
выпуклое мн-ство простой структуры,
т.е. подмн-тво, кот. задается с помощью
простейших ограничений на одну переменную
(
).
Задача наз. основной задачей выпуклого
программирования.
(1), в
которой
– вектор-функция,
ф-ции
– выпуклые ф-ции;
–
выпуклое мн-ство простой структуры,
т.е. подмн-тво, кот. задается с помощью
простейших ограничений на одну переменную
(
).
Задача наз. основной задачей выпуклого
программирования.
Опр. Мн-тво
планов основной задачи выпуклого
программирования регулярно,
если существует вектор
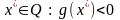 (2)
(2)
Усл.(2) наз. условием
Слейтера.
Геометрич.(2) означает,что у зад.(1)
существует такой план
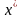 ,
кот. явл. внутренней точкой по основным
ограничениям.
,
кот. явл. внутренней точкой по основным
ограничениям.
Теорема 2.
(Куна-Таккера)
Для того, чтобы
был оптимальный план основной задачи
выпуклого программирования, для которой
выполняется условие регулярности (2),
необходимо и достаточно, чтобы существовал
такой вектор
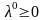 такой, что пара
является седловой точкой функции
Лагранжа и при этом выполн. условие
дополняющей не жесткости:
такой, что пара
является седловой точкой функции
Лагранжа и при этом выполн. условие
дополняющей не жесткости:
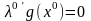 .
.
Доказательство.
Необходимость.
Пусть
–
оптимал. план (1) и выполняется
. Тогда по нему и параметрам зад.(1)
построим три подмножества:
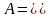
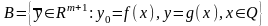 .
Ясно, что мн-тво
.
Ясно, что мн-тво
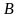 явл. границей мн-тва
явл. границей мн-тва
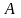 ,
т.е.
,
т.е.
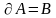
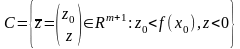
1. Доказываем, что
множества
и
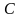 выпуклые.
выпуклые.
2. Докажем, что множества и не пересекаются.
3. Докажем, что
вектор
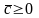 .
.
4. Докажем, что в
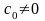 ,
а так как
,
то
,
а так как
,
то
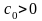 .
.
5. Докажем, что на выполняется условие .
Таким образом, пара удовлетворяет (3) и, следовательно, является седловой точкой функции Лагранжа.
Ч.т.д.
4. Критерий оптимальности для гладкой выпуклой задачи.
Рассм. зад.
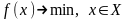 (1),
– выпуклая ф-ция,
– выпуклое мн-во,
(1),
– выпуклая ф-ция,
– выпуклое мн-во,
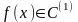 .
Ф-цию
переменных, около некоторой т.
(в малой окрестности) можно разложить
в ряд
.
Ф-цию
переменных, около некоторой т.
(в малой окрестности) можно разложить
в ряд
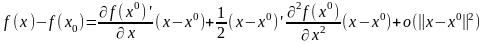 (2)
(2)
Разложение (2)
справедливо лишь для
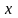 в малой окрестности точки
,
и в этой же окрестности справедливо
утверждение: знак выражения слева
необходимо и достаточно совпадает со
знаком первого ненулевого слагаемого
справа. Это утверждение легко доказывается
методом от противного.
в малой окрестности точки
,
и в этой же окрестности справедливо
утверждение: знак выражения слева
необходимо и достаточно совпадает со
знаком первого ненулевого слагаемого
справа. Это утверждение легко доказывается
методом от противного.
Теор.3. Для
того чтобы
был оптимальным планом задачи (1)
необходимо и достаточно, чтобы
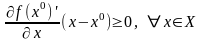 (3).
А в случае, когда
(3).
А в случае, когда
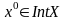 ,
то (3) эквивалентно условию стационарности
,
то (3) эквивалентно условию стационарности
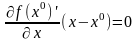 .
(4)
.
(4)
Док-во. Необходь.
Пусть
– оптимал. план зад.(1). Возьмем произвол.
точку
 и построим точку
и построим точку
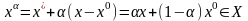 .
Если
достаточно мало, то т.
.
Если
достаточно мало, то т.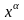 лежит в сколь угодно малой окр-ности
.
Запишем разложение:
лежит в сколь угодно малой окр-ности
.
Запишем разложение:
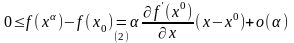 .
Т.к. левая часть равенства
.
Т.к. левая часть равенства
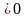 ,
то неотрицательно и первое слагаемое
справа. А так как
,
то неотрицательно и первое слагаемое
справа. А так как
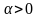 ,
то приходим к (3).
,
то приходим к (3).
Пусть теперь к
тому же
– внутренняя точка. Построим вектора
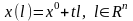 .
При достаточно малом
.
При достаточно малом
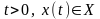 .
Подставляя его в (3):
.
Подставляя его в (3):
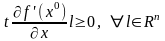 .
Т.к.
.
Т.к.
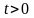 ,
то
,
то
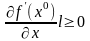 .
Из этого нерав-тва следует (4).
.
Из этого нерав-тва следует (4).
Если предположить
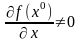 и положить
и положить
 ,
то придем к противореч.
,
то придем к противореч.
Достаточность.
Пусть выполняется (3). Докажем, что
– оптимальный план задачи (1). Так как
функция
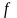 – гладкая и выпуклая, то для нее
выполняется гладкий критерий выпуклости:
– гладкая и выпуклая, то для нее
выполняется гладкий критерий выпуклости:
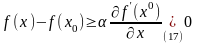
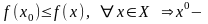 оптимальный
план.
оптимальный
план.
Ч.т.д.
Из этой теоремы и
теоремы Куна-Таккера следует схема
исследования гладкой основной задачи
выпуклого программирования (
,
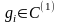 ).
).
