66. Мгновенный центр ускорений.

При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение какой-нибудь точки А фигуры и величины и , следующим путем:

1) находим значение угла , из формулы ;

2) от точки А под углом , к вектору проводим прямую АЕ (рис.45);

при этом прямая АЕ должна быть отклонена от в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ;3) откладываем вдоль линии АЕ о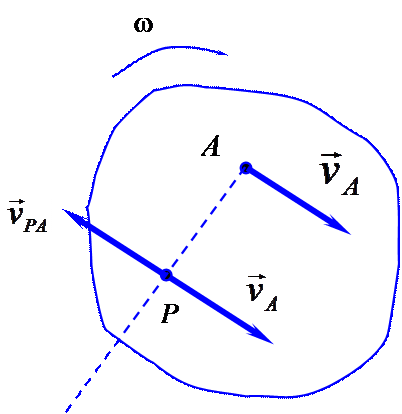 трезокюAQ, равный . Рис.45Построенная таким путем точка Q и будет мгно­венным центром ускорений. В самом деле, известно что ,

где численно . Подставляя сюда значение AQ находим, что . Кроме того, вектор должен образовывать с ли­нией AQ угол , следовательно, вектор параллелен , но направлен в про­тивоположную сторону. Поэтому и .Если точку Q выбрать за полюс, то так как , ускорение любой точки М тела, будет .

При этом численно .

Следовательно, ускорения точек плоской фигуры определяются в данный мо­мент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом ,

т.е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгно­венного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.46.

Следует иметь в виду, что положения мгновенного центра скоростей Р и мгно­венного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.47), причем скорость его центра С постоянна ( ), то мгновенный центр скоростей находится в точ­ке Р ( ), но при этом, как было показано ; следовательно, точка Р не является одновременно мгновенным центром ускорений.

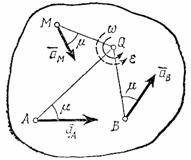Рис.46 Рис.47Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она дви­жется равномерно и прямолинейно и . Центры скоростей и ускорений сов­падают тогда, когда фигура (тело) вращается вокруг неподвижной оси.64. 10.3. Мгновенный центр скоростей Теорема. При непоступательном движении плоской фигуры существует жестко связанная с ней точка, скорость которой в данный момент движения равна нулю. Эта точка является мгновенным центром скоростей.Доказательство. Отложим перпендикуляр к скорости в точке , как указано на рис. 10.7 и выберем на нем точку на расстоянии: . По теореме о скоростях точек тела при плоском движении: , где .Следовательно, . 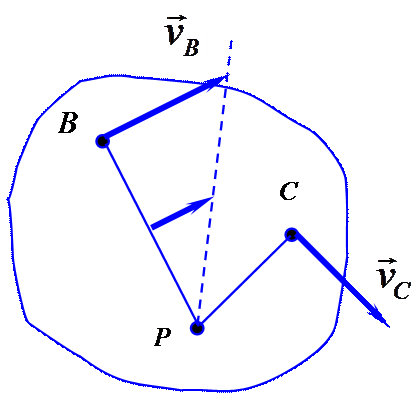Теорема доказана.В ыбирая мгновенный центр скоростей за полюс, нетрудно убедиться, что скорость любой точки плоской фигуры находится как скорость во вращательном движении вокруг этого центра (рис. 10.8).

, , ,

,

, ,

т.е. скорости пропорциональны расстояниям до мгновенного центра скоростей. Через мгновенный центр скоростей проходит мгновенная ось вращения тела.

Рассмотрим основные способы нахождения мгновенного центра скоростей.

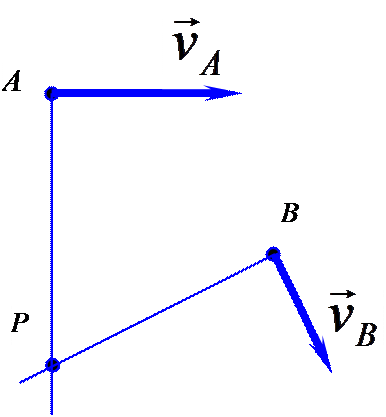
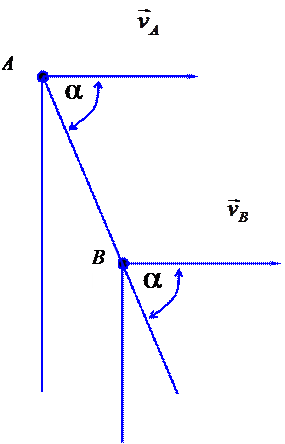
1. Известны направления скоростей двух точек тела, и они не параллельны. Мгновенный центр скоростей лежит на пересечении перпендикуляров к скоростям (рис. 10.9).

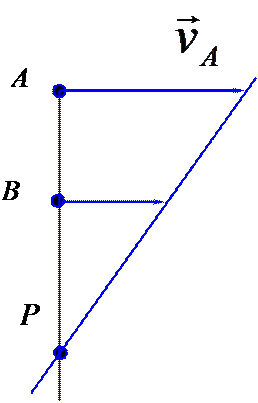
2. Перпендикуляры к скоростям двух точек тела совпадают (рис. 10.10, 10.11). Мгновенный центр скоростей находится из условия пропорциональности скоростей расстояниям до этого центра. Если скорости равны, то мгновенный центр скоростей не существует и тело совершает мгновенно-поступательное движение ( ).

3. Скорости двух точек тела параллельны, а перпендикуляры к ним не совпадают (рис. 10.12). В этом случае тело совершает мгновенно-поступательное движение. По следствию из теоремы о скоростях при плоском движении

, т.е.: и .

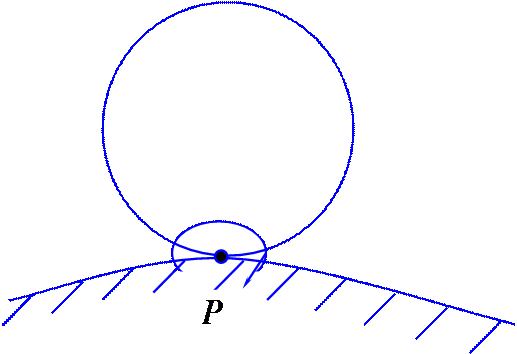
 4.      Качение без скольжения по неподвижной поверхности (нет проскальзывания) (рис. 10.13). Мгновенный центр скоростей находится в точке касания тела с неподвижной поверхностью.