Доказательство

Если f(x; y) непрерывна на D, то существуют наименьшее m и наибольшее М значения функции f(x; y), т.е.        по свойству 6 имеем:

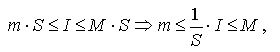
то есть число I/S находится между m и М.

Но непрерывная функция f(x; y) принимает все промежуточные от m до М значения  существует точка M_* D:

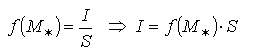
40 Свойства двойного интеграла

^{Линейность.} _∫∫ ^{(α ⋅ f ( x, y ) + β ⋅ g ( x, y)) dxdy = α ⋅} _∫∫ ^{f ( x, y)dxdy + β ⋅} _∫∫ ^{g ( x, y)dxdy ;}

D D D

(Имеется в виду, что если существуют оба интеграла в правой части, то существует интеграл и в левой части).

  1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D₁ и D₂, то функция f(x, y) интегрируема в каждой из областей D₁ и D₂, причем

     2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем

     3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

     4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

Применение: Обычный определенный интеграл от функции одной переменной хорошо знаком студентам первого курса и имеет многочисленные приложения в различных отраслях знаний. Однако, существует иного задач в геометрии, физике, экономике, для которых недостаточно обычного определенного интеграла – интеграла по одномерному координатному отрезку. Таковы, например, задачи о вычислении площади поверхности (не являющейся поверхностью вращения), объема тела в общем случае, массы пластинки или тела переменной плотности. Для решения этих задач нужно уметь интегрировать по плоской или даже пространственной области. Такие интегралы называются двойными и тройными соответственно.

41 Вычисление двойного интеграла в декартовых координатах.

(а) Пусть область D задается неравенствами (см. Рис. 3):

^{a ≤ x ≤ b,}

^y_нижн ^{( x) ≤ y ≤ y}_верхн ^{( x) , (1)}

где функции

^y_нижн ^{( x) и}

^y_{в ер х н} ^{( x)}

непрерывны на отрезке [a; b] , и функция

f ( x, y)

непрерывна в области D. Тогда двойной интеграл от функции

f ( x, y)

по области D

42 Интегральная сумма

Пусть на отрезке определена вещественнозначная функция .

Рассмотрим разбиение отрезка — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок на n отрезков . Длина наибольшего из отрезков , называется шагом разбиения, где — длина отрезка.

Отметим на каждом отрезке разбиения по точке . Интегральной суммой называется выражение .

Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора , то это число называется интегралом функции на отрезке , т.е. .

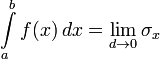Теорема существования тройного интеграла. Пусть в пространстве Oxyz задана ограниченная замкнутая область (объём)  V, и пусть на области V определена функция .

Разобьём область V произвольным образом на  подобластей  (не имеющих общих внутренних точек). Символом  будем обозначать объём области ; символом  обозначим наибольший из диаметров областей : .

В каждой из подобластей  выберем произвольную точку , вычислим в этой точке значение функции , и составим интегральную сумму .

Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области V на подобласти , ни от выбора точек , то функция  называется интегрируемой по области V, а значение этого предела называется тройным интегралом от функции по области V и обозначается .

Если расписать значение  через координаты точки , и представить  как , получим другое обозначение тройного интеграла: . Итак, кратко, .

Теорема существования тройного интеграла. Если подынтегральная функция  непрерывна на области V, то она интегрируема по этой области.

43 Свойства тройного интеграла по смыслу и доказательству полностью аналогичны свойствам определённого и двойного интегралов.

    Линейность. Если функции ,  интегрируемы по области V, то их линейная комбинация  тоже интегрируема по , и  .

Аддитивность. Если область  является объединением двух областей  и , не имеющих общих внутренних точек, то .

Интеграл от единичной функции по области V равен объёму этой области: .

45 - 47 Криволинейный интеграл первого рода

Свойства

1. Линейность:

2. Аддитивность: если в одной точке, то

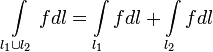
3. Монотонность: если на , то

4. Теорема о среднем для непрерывной вдоль функции :

Очевидно, что: .

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: .

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление

Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла первого рода. Тогда

.

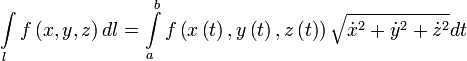Здесь точкой обозначена производная по : .