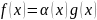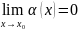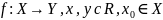2) Предел произведения двух переменных величин равен произведению пределов этих величин:

 (а_n • b_n) =   а_n •   b_n.

Пример.

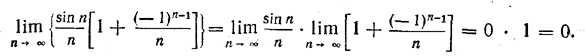
И эта теорема верна не только для двух, но и для произвольного фиксированного числа сомножителей.  Например,

 (а_n • b_n • c_n • d_n) =   а_n •   b_n•   c_n •   d_n

3) Формулировка

Пусть   и   — две последовательности вещественных чисел, причём   положительна, неограничена и строго возрастает (хотя бы начиная с некоторого члена). Тогда, если существует предел

,

то существует и предел

,

причём эти пределы равны.

[Править]Доказательство

Допустим сначала, что предел равен конечному числу  , тогда для любого заданного   существует такой номер  , что при   будет иметь место

Значит для любого   все дроби

лежат между этими же границами. Так как знаменатели этих дробей положительны (в силу строго возрастания последовательности  ), то между теми же границами содержится и дробь

,

числитель которой есть сумма числителей написанных выше дробей, а знаменатель — сумме всех знаменателей. Итак, при 

.

Теперь рассмотрим следующее тождество (проверяемое непосредственно):

,

откуда имеем

.

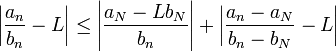Второе слагаемое при   становится меньше  , первое слагаемое также станет меньше  , при  , где   — некоторый достаточно большой номер, в силу того, что  . Если взять  , то при   будем иметь

,

что и доказывает наше утверждение.

Случай бесконечного предела можно свести к конечному. Пусть, для определённости

,

из этого следует, что при достаточно больших 

и

,

причём последовательность   строго возрастает (начиная с определённого номера). В этом случае, доказанную часть теоремы можно применить к обратному отношению  :

,

откуда и следует, что

.

Случай предел равен  , то нужно рассмотреть последовательность  .

14. Теорема о пределе сложной функции.

y=f(x), x ϵ X,

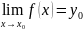
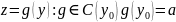
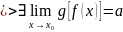
14. Односторонние пределы

Символом   обозначается левосторонний предел, в котором переменная x, приближаясь к a, принимает значения x < a. Соответствующий предел  называется левосторонним пределом функции f (x) в точке x = a.

Символом   обозначается правосторонний предел, в котором переменная x, приближаясь к a, принимает значения x > a. Соответствующий предел  называется правосторонним пределом функции f (x) в точке x = a.

14. ??????????????????????????

??????????????????????????

??????????????????????????

17. 

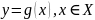
Опр.1

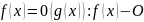
От функции g(x)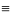 f(x) – ограничена функцией g(x) на множестве X

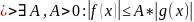
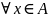
Опр.2

1. 

2. 

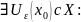
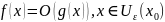
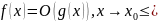
Утв.

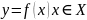
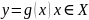
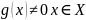
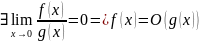
18. Функции f(x) и g(x) называются эквивалентными при x→ a, если 

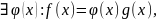
где .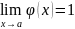

Иначе говоря функции эквивалентны при x→ a, если предел их отношения при x→a равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x  0

tg x ~ x, x  0,

e^x-1~ x, x 0

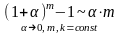
ln (1+x)~ x, x 0

18. 

Функция f имеет производную в т.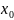 (f- дифференциальная в т. ) f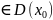

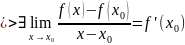
Обозначения: y ^' ,   f ^' (x_o),    ,    .

18. Дифференциалом функции y=f(x) в точке называется главная, линейная относительно ∆x, часть приращения функции в точке:

dy=A∆x

Если функция y=f(x) дифференцируема в данной точке , то она непрерывна в данной точке

18. Если функции u=u(x) и v=v(x) дифференцируемы в точке x, то сумма, разность, произведение и частное этих функций (частное при условии, что 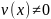) также дифференцируемы в этой точке и имеют место следующие формулы:

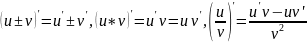
18. Если функция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).

y '_x = y '_x· u '_v· v '_x = f '_u (u)·u '_v (v)·v '_x (x)

Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную , т.е. справедлива формула .

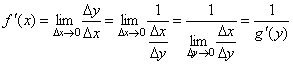
18. Производная сложной функции

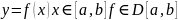
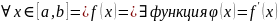
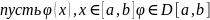
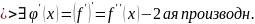
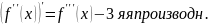
1ая производная – мгновенная скорость точки

2ая производная – ускорение движущейся точки в данный момент

Дифференциал сложной функции

dy= f’(x)dx дифференциал первого порядка

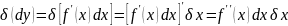дифференциал второго порядка

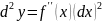
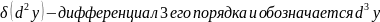
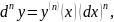n=1,2,3….

18. ?????Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.?????

Теорема

Если функция f(x) дифференцируема на интервале (а,b) и f’(x)≥0 (f’(x)≤0) на (a,b), то функция f(x) не убывает (не возрастает)

18. График функции y=f(x) имеет на (a,b) выпуклость, напрвленную вниз(вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (a, b)

\\Теорема Если функция y=f(x) имеет на интервале (a, b) вторую производную и f’’(x)≥0 (f’’(x)≤0) во всех точках (a, b), то график функции y=f(x) имеет на (a, b) выпуклость, направленную вниз (вверх).

Точка M(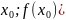 называется точкой перегиба графика функции y=f(x), если в точке М график имеет касательную, и существует такая окрестность точки , в пределах которой график функции y=f(x) слева и справа от точки имеет разные направления выпуклости.

\\\ Теорема (необходимое условие точки перегиба)

Пусть график функцииy=f(x) имеет перегиб в точке и пусть функция y=f(x) имеет в точке непрерывную вторую производную. Тогда f’’(x) в точке обращается в нуль, т.е. f’’( )=0

27 Напомним определение локального экстремума функции.

      Определение 7.4   Пусть функция   определена в некоторой окрестности  ,  , некоторой точки   своей области определения. Точка   называется точкой локального максимума, если в некоторой такой окрестности   выполняется неравенство   (  ), и точкой локального минимума, если    .     

Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.

Следующая теорема даёт необходимое условие того, чтобы точка   была точкой локального экстремума функции  .

        Теорема 7.4   Если точка   -- это точка локального экстремума функции  , и существует производная в этой точке  , то  .

Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5).    

Утверждение теоремы можно переформулировать так:

если функция   имеет локальный экстремум в точке  , то либо  1)  , либо  2) производная   не существует.

Точка   называется критической точкой функции  , если   непрерывна в этой точке и либо  , либо   не существует. В первом случае (то есть при  ) точка   называется также стационарной точкой функции  .

Итак, локальный экстремум функции   может наблюдаться лишь в одной из критических точек этой функции.

28-29

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.