4. Частные производные функции нескольких переменных и их геометрическая интерпретация.

Частные производные первого порядка. Пусть функция   определена в области   и  . Тогда при малых   определено ее частное приращение по  :  .         Определение. Частной производной функции   по переменной    в точке   называют предел ,если он существует.    Частную производную по   обозначают одним из следующих символов: .Аналогично определяется частная производная по   и вводятся ее обозначения. Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной. Пример. Найти частные производные функции  .  Имеем:      . Частные производные высших порядков. Рассматривая частные производные   и   как функции от  , приходим к понятиям частных производных второго порядка. А именно, выражения ,      называют частными производными второго порядка функции   по   и по   соответственно, а выражения

,      – смешанными частными производными второго порядка функции  . Их обозначают также символами:  ,  ,   и  . Аналогично определяют частные производные 3-го порядка (их будет 8=2³ ), 4-го порядка (их будет 16=2⁴ ) и т.д. Теорема 4. Если в некоторой окрестности точки  функция   имеет смешанные частные производные   и  , причем эти производные непрерывны в точке  , то они равны в этой точке: = . Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции   не зависят от порядка дифференцирования в точке  .Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.

Геом интерпретация:Геометрический смысл ЧП-ой состоит в следующем : значение   ЧП-ой по переменной «х» = тангенсу угла наклона на касательной проведённой к кривой получаемой пересечением  поверхностей Z=f(x,y) и  плоскости у=у0.Анологично опр-ся геометрический смысл ЧП-ой по переменной «у». Значение ЧП-ой по переменной «у» = тангенсу угла наклона  касательной проведённой к кривой    к-рая получается при пересечении  поверхности с плоскостью х=х0

5. Производная сложной функции.

Предположим, что в уравнении z = F(u,v)(1) u и v являются функциями независимых переменных хиу: (2)В этом случае z есть сложная функция от аргументов х и у. Конечно, z можно выразить и непосредственно через х, у, а именно: (3)Предположим, что функции имеют непрерывные частные производные по всем своим аргументам и поставим задачу: вычислить и исходя из уравнений (1) и (2) и не пользуясь уравнением (3). Дадим аргументу х приращение ∆х, сохраняя значение у неиз­менным. Тогда в силу уравнения (2) и и v получат приращения ∆_хи и ∆_xv. Но если и и v получают приращения ∆_хи и ∆_xv, то и функция z = F(u_, v) получит приращение ∆z. Разделим все члены этого равенства на ∆х: . Если (в силу непрерывности функ­ций u и v). Но тогда и у₂ тоже стремятся к нулю. Переходя к пределу при ∆х -> 0, получим Если бы мы дали приращение переменной у, а х оставили неизменным, то с помощью аналогичных рассуждений нашли бы Производная неявной функции Начнем рассмотрение этого вопроса с неявной функции одной переменной. Пусть некоторая функция у от х определяется уравнением F(x,y)= о(1). Докажем следующую теорему. Теорема. Пусть непрерывная функция у от х задается не­явно уравнением F(x,y)= о. где F(x_y у)_у F'_x(x_y у), F'_x(x, у)— непрерывные функции в некото­рой удовлетворяют уравнению (1); кроме того_, в этой точке F'_y (х_у у)≠0. Тогда функция у от х имеет производную . Доказательство. Пусть некоторому значению х соответ­ствует значение функции у. При этом (1). Дадим независимой переменной х приращение ∆х. Функция у получит приращение ∆у_у т. е. значению аргумента х+∆х соот­ветствует значение функции у + ∆у. В силу уравнения (1) будем иметьF(x + ∆x_, у + ∆у) = 0. Следовательно, F(x+∆x, y+∆y) — F(x, y) = 0 Левую часть последнего равенства, являющуюся полным прира­щением функции двух переменных, по формуле можно переписать так: где Ƴ₁ и Ƴ₂ стремятся к нулю при ∆х и ∆у_, стремящихся к нулю. Так как левая часть последнего выражения равна нулю, можно написать Разделим последнее равенство на ∆х и вычислим Устремим ∆x к нулю. Тогда, учитывая, что при этом Ƴ₁ и Ƴ₂ также стремятся к нулю и что в пределе получим Мы доказали существование производной Ƴ_х от функции, задан­ной неявно, и нашли формулу для ее вычисления.

Производная по направлению.Рассмотрим в области D функцию u=u(x,y,z) и точку M(x,у,z). Проведем из точки М вектор S, направляющие коси­нусы которого cosα, cosβ, cosƳ. На векторе S на расстоянии ∆s от его начала рассмотрим точку M₁ (х+ ∆х, у + ∆у, z+∆z). Таким образом, Будем предполагать, что функция и(х, у, z) непрерывна и имеет непрерывные производные по своим аргументам в области D. полное приращение функции представим так: (1) где Ɛ₁, Ɛ₂ и Ɛ₃, стремятся к нулю при ∆s->0. Разделим все члены равенства (1) на ∆s: (2) Очевидно, что Следовательно, равенство (2) можно переписать так: (3)Предел отношения при при ∆S->0 называется производной от функции и = и(х, у, г) в точке (х, у, г) по направлению S и обозначается , т.е. (4) Таким образом, переходя к пределу в равенстве (3), получим (5) Из формулы (5) следует, что, зная частные производные, легко найти производную по любому направлению S. Сами частные производные являются частным случаем производной по направлению. Так, например, при α=0,β= ,Ƴ= получаем: Градиент. В каждой точке области D, в которой задана функция u= u(x,y,z) определим вектор, проекциями которого на оси координат являются значения частных производных 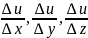этой функции в соответствующей точке: Этот вектор называется градиентом функции u= u(x,y,z) Говорят, что в области D определено векторное поле градиентов. Докажем, далее, следующую теорему, устанавливающую связь между гради­ентом и производной по направлению. Теорема. Пусть дано скалярное поле u= u(x,y,z) и опре­делено в этом скалярном поле поле градиентов Производная по направлению некоторого вектора S равняется проекции вектора grad и на вектор S. ДоказательствоРассмотрим единичный вектор S⁰, соот­ветствующий вектору S: S° = icos α+jcos β+ kcosƳ. Вычислим скалярное произведение векторов gradu и S⁰:(grad и, s°)= cosα+ cosβ+ cos Ƴ.(2) Выражение, стоящее в правой части этого равенства, есть производная от функции и (х, у, г) по направлению вектора S. Следо­вательно, мы можем написать (grad и, s°) = 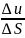Если обозначим угол между векторами gradu и S⁰ через ϕ ,то можем написать |gradu|cosϕ = Теорема доказана.

6. Полный дифференциал.Пусть функция Z (x,y) имеет непрерывные частные производные .Выразим полный дифференциал функции f через частные производные:ΔZ = f (x+Δx, y+Δy) – f (x, y) = [ f (x+Δx, y+Δy) – f (x, y+Δy)] + [f(x+Δx, y+Δy) – f(x, y)] (1)в соответствии с теоремой Лагранжа сущ. точка ∈[x, x+Δx] :f(x+Δx, y+Δy) – f(x, y+Δy) = Δx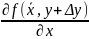 (2) f (x+Δx, y+Δy) – f (x, y)= Δy (3)y [y, y+Δy]Подставим (2) и (3) в (1):ΔZ = Δx + Δy (4)Учитывая, что непрерывны дифференциалы Δx и Δy к нулю: , (5); (5)Используя выражения (5) запишем: ; (6)Используя выражение (6), получим:

ΔZ = (7);Сумма двух слагаемых бесконечно малая более высокого порядка, чем

Используя это, дадим следующее определение: Z = f(x,y) для которого полное приращение ΔZ в данной точке (x, y) может быть представлено в виде суммы двух слагаемых: линейная часть Δx и Δy и величины бесконечно малой высшего порядка относительно p, то данная функция называется дифференцируемой, а линейная часть приращения называется полным дифференциалом данной функции:

(8) Под дифференциалом будем понимать dx и dy: Запишем следующим образом: (9)Дифференциал функции любого числа переменных вычисляется с помощью этой формулы.7. Применение полного дифференциала в приближенных вычислениях.Пусть функция z = f(x,y) дифференцируема в точке (x,y)Найдем полное приращение этой функции. ∆z = f(x+∆x, y+∆y)-f(x,y).Откуда f(x+∆x, y+∆y)= f(x,y)+ ∆z. (1)Мы имели приближенную формулу ∆z≈dz (2)Где dz= ∆x+ ∆y (3)Подставляя в формулу (1) вместо ∆z развернутое выражение для dz, получим приближенную формулу f(x+∆x,y+∆y)≈f(x,y)+ ∆x+ ∆y (4)

8.Инвариантность формы первого дифференциала. Дифференциал сложной функции.Инвариантность формы первого дифференциала.Если x - независимая переменная, то dx = x - x₀ (фиксированное приращение). В этом случае имеем df(x₀) = f'(x₀)dx.     (3) Если x = φ(t) - дифференцируемая функция, то dx = φ'(t₀)dt. Следовательно, т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.Теорема: Пусть и функции x = x(u, v)Î , y(u, v)Î = x(u₀, v₀), y₀ = y(u₀, v₀).Тогда f(x(u, v), y(u, v))ÎD(u₀, v₀) и ; Доказательство: Рассмотрим разности: из которых следует, что

f(x(u, v), y(u, v)) - f(x(u₀, v₀), y(u₀, v₀)) = Следовательно, по определению дифференцируемости функция двух переменных: f(x(u, v), y(u, v))ÎD(u₀, v₀) и

9. Геом. Смысл полного дифференциала.1 переменная: Приращение ординаты касательной.2 переменных: Приращение аппликаты касательной

_{Уравнение касательной плоскости:}