1. Введение:

Сопротивление материалов относится к наукам о прочности, в ко­торой изучаются законы деформирования и разрушения тел с целью создания методов оценки прочности элементов конструкций.

Сопротивление материалов - это наука об основах инженерных расчетов элементов конструкций на прочность, жесткость и устойчивость при обеспечении необходимой долговечности и эконо­мичности.

Сопротивление материалов является наукой экспериментально-теоретической, она широко использует опытные данные и теоретиче­ские исследования, в ней применяются методы теоретической меха­ники и математического анализа, используются данные из разделов физики, материаловедения.

Реальный объект и расчетная схема

Под надежностью предполагают, что конструкция является прочной, жесткой и устойчивой, при гарантированной долговечности.

Прочность - это способность конструкции сопротивляться разрушению при действии на нее внешних сил (нагрузок).

Жесткость - способность конструкции сопротивляться деформации.

Устойчивость - св-во системы сохранять свое начальное рав­новесное положение при внешних воздействиях.

Долговечность конструкции состоит в ее способности сохранять необходимые для эксплуатации свойства в течение определенного от­резка времени.

Идеализированная схема реального объекта, отражающая наиерпарапрапрапболее существенные свойства конструкции называет расчетной схемой. Основными факторами, определяющими расчетную схему являются: элементы конструкции, внешние силы, условия закрепления.

В сопротивлении материалов все элементы конструкции условно делятся на четыре типа: стержень, пластина, оболочка, массивное те­ло.

Стержнем называется тело, длина которого значительно больше его поперечных размеров (рис. 2.1.1).

Элемент конструкции, ограниченный двумя поверхностям, от­стоящими друг от друга на малом расстоянии называла оболочкой (рис. 2.1.2).

Пластина – плоский элемент, толщина которого меньше других размеров (рис. 2.1.3).

Элемент конструкции, размеры которого во всех направлениях сравнимы по величине, называется массивным телом (рис. 2.1.4).

Внешние силы возникают в результате взаимодействия рассматри­ваемого тела с окружающими телами и средой. Различают объемные и поверхностные силы. Объемные силы непрерывно распределены по всему объему тел (вес, силы инерции, магнитные силы). Поверхност­ные силы приложены к поверхности тела.

Соприкосновение тел всегда происходит по некоторой площадке. Поэтому все поверхностные силы являются распределенными силами. Если тела соприкасаются по узкой длинной площадке, то считается, что поверхностная сила действует по линии. Такая сила называется погонной распределенной. Если размеры площадки, по которой про­исходит взаимодействие тел, малы по сравнению с размерами тела, то считается, что сила действует в точке и она называется сосредоточенной.

По характеру изменения во времени, различают нагрузки статические и динамические. Статические нагрузки являются постоянными, либо медленно изменяют свою величину или точку приложения (направление). Возникающие при этом ускорения тела (силы инерции) можно не учитывать. Динамические нагрузки - изменяется во време­ни с ускорением, при этом силы инерции должны быть учтены, так как они достигают значительных величин.

При рассмотрении реального объекта в число внешних сил включаются не только заданные внешние нагрузки, но и реакции опор.

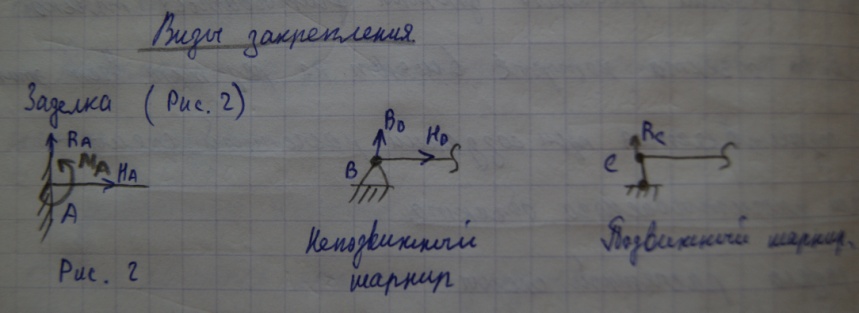
При закреплении стержней часто используют шарнирно-подвижные опоры, шарнирно-неподвижные опоры и заделку (рис 2).

Основные гипотезы сопротивления материалов

Предполагается, что все материалы являются:

Однородными. Однородный материал имеет одинаковые свойст­ва во всех точках тела.

Сплошными. Сплошными называются среды, не имеющих тре­щин и пустот.

Изотропными. Тело считается изотропным, если его механические свойства одинаковы во всех направлениях.

Д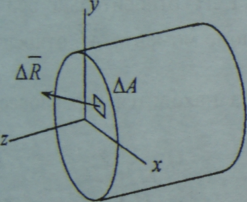 еформируемыми. В сопротивлении материалов учитывается способность тела деформироваться, т.е. под действием сил изменять свои начальные размеры и форму. При этом деформации приниаются малыми по сравнению с линейными размерами тела.

Абсолютно упругими. Упругостью называется свойство тел восстанавливать свои первоначальные форму и размеры после снятия нагружения.

Помимо рассмотренных выше допущений в сопротивлении мате­риалов вводится ряд гипотез, позволяющих значительно упростить расчет:

Принцип независимости действия сил (принцип суперпозиции): результат совместного действия нескольких сил равен сумме резуль­татов действия каждой из них в отдельности.

П ринцип Сен-Венана (принцип локальности): на достаточном удалении от места приложения силы особенности способа приложе­ния этой силы можно не учитывать.

Гипотеза Бернулли (гипотеза плоских сечений): поперечные се­чения стержня, плоские и нормальные к оси стержня до приложения к нему силы, остаются плоскими и нормальными к его оси при дейст­вии силы.

2. Внутренние силы.

В любом материала имеются внутренние межатомные силы взаимодействия. При деформации тела изменяется взаимодейст­вие между его частицам. Си­лы взаимодействия, возни­кающие между частями тела при его деформировании, на­зываются внутренними сила­ми.

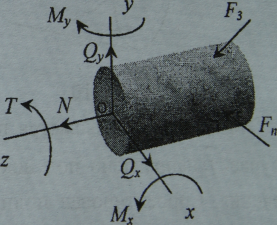
Для определения внутренних сил применяется метод сечений: Пусть некоторое призматическое тело на­ходится в равновесии под действием системы внешних сил. Рассечем (мыс­ленно) тело на две части плос­костью, перпендикулярной к продольной оси и отбросим одну из них. Рассмотрим равновесие оставшейся части. Заменим действие отбро­шенной части, на оставшуюся, некоторой системой сил. Распределенные по сечению силы заменим их равнодействующими: главным вектором R и главным моментом М. Введем ортогональную систему координат, так чтобы ось Оz сов­падала с продольной осью тела, а оси Ох и Оу - расположены в попе­речном сечении. Разложим главный вектор R и главный момент М на составляющие, которые называются внутренними си­лами.

В общем случае в поперечном сечении действуют шесть сил: N - продольная сила (Проекция вектора R на ось z); Qx, Qy – поперечные силы (проекции вектора R на оси х, у соответственно); Mz=T - кру­тящий момент (составляющая момента М относительно си z); Mx, My - изгибающие моменты (составляющие момента М относительно осей х, у).

Т ак как рассматриваемая часть тела находится в равновесии, то должны выполняться шесть урав­нений равновесия:

; ;

; ;

; ;

Из этих уравнений находят N, Qx, Qy, Mx, My, T.

Понятия о напряжениях и деформациях.

Выделим на плоскости сечения площадку C, на которой будет действовать внутренняя сила R (рис.). Величина отношения называется средним напряжением на площадке ∆А. Напряжение в точке А получим устремив ∆А к нулю: .

Эта величина называется полным напряжением в точке. В общем случае р направлено под некоторым углом а к нормали плоскости сечения. Спроектировав полное напряжение на нормаль к сечению, получим нормальное напряжение в точке σ = р cos а. Проекция пол­ного напряжения на плоскость сечения - касательное напряжение в точке τ = р sin а (рис.).

К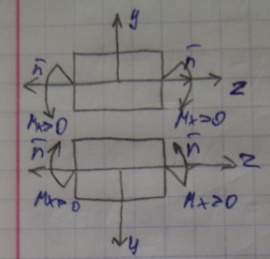 асательное напряжение может быть разложено по направлениям осей х и у на составляющие τ_Х и τy (рис.).

Нормальные и касательные напряжения в каждом поперечном се­чении тела связаны с внутренними силами, действующими в этом се­чении.

Выделим элементар­ную площадку dA. Действующие по этой площадке напряжения σ, τ_Х , τy , создают элементарные силы σdA, τ_ХdA, τydA и элемен­тарные моменты относительно осей координат: dMx=(σdA)y, dMy=(σdA)x, dT=(τydA)x-(τ_ХdA)y.

Суммируя все элементарные силы и моменты, действующие в се­чении, получим следующие интегральные зависимости:

; ; Qy ; Mx ; ; ;

Проведем через некоторую произвольную точку а тела в направлениях осей х и у бесконечно малые отрезки ав и ас, длиной dx и dy (рис).

П осле деформации точка а переместится в а1. Величина аа1 называется линеиным перемещением точки а. Отрезки ав и ас займут новые положения a1b1 и a1c1. Их длины изменятся и станут равными dx₁=dx+∆dx, dy₁ = dy+∆dy. Величины ∆dx и ∆dy называются абсолютными линейными деформациями. Отношение приращения длины отрезка к его начальной длине называется относительной линейной деформацией.

Т ак, относительная деформация в направлении оси х равна . Аналогично, в направлении оси у .

Угол между отрезками ав и вс после деформации изменится и ста­нет равным a1. Изменение этого угла γ_xy=a-a1 - называется угло­вой деформацией.

В любой точке тела можно выделить отрезки dx, dy, dz в направле­нии осей координат и определить линейные деформации εx, εy, εz, а также изменения углов между этими отрезками - угловые деформа­ции γ_xy, γ_xz, γ_yz. Совокупность εx, εy, εz, γ_xy, γ_xz, γ_yz определяет де­формированное состояние в точке.

Правила знаков для напряжений и внутренних сил

Продольная сила N является положительной, если она растягивает стержень.

Крутящий момент Т считается положительным, если он стремиться повернуть балку против часовой стрелки при взгляде на сечение со стороны продольной оси.

При изгибе с одной стороны волокна растягиваются, с другой сжимаются. Внутри балки будет слой, который не растягивается и не сжимается – нейтральный слой.

Момент Мх считается положительным, если он растягивает волокна балки с положительной координатой у. Аналогично с Му.

Нормальное напряжение σ считается положительным, если оно направлено от сечения, т.е. вызывает растяжение.

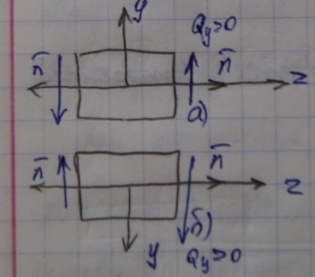
В сечении, нормаль к которому направлена в сторону оси Oz, по­ложительные касательные напряжения τ_Х , τy действуют в сторону осей Ох, Оу, соответственно (рис).

В сечении, нормаль к которому направлена в сторону противопо­ложную оси Oz, положительные касательные напряжения τ_Х , τy дей­ствуют, соответственно, в стороны, противоположные осям Ох, Оу (рис.).

Поперечные силы Qx, Qy будут положительными, если в сечении, нормаль к которой совпадает с направлением оси Oz, они направлены в сторону положительного направления осей Ох, Оу, соответственно (рис. ).

В сечении, нормаль к которому направлена противоположно оси Oz (рис. ), положительные поперечные cum Qx, Qy, направле­ны в стороны, противоположные осям Ох, Оу.

Рама - стержневая система, составленная из прямолинейных стержней жестко соединенных между собой.

Дифференциальная зависимость между изгибающим моментом Мх, поперечной силой Qy и распределенной нагрузкой q.

Вырежем из балки элемент длиной dz. В левой части элемента будут действовать изгибающий момент Мх, поперечная сила Qy. В правом сечении действуют Mx+dMx, Qy+dQy. Момент и сила получили приращение. Составим уравнение равновесия:

Пренебрегая подчеркнутыми бесконечно-малыми величинами получим:

Следствия из дифф. Зависимости величин Mx,Qy,q.

1. В сечении, где Qy=0; Mx принимает экстремальные значения (min или max). dMx/dz=0 – условие экстремальности.

2. На участке, где Qy>0, изгибающий момент увеличивается и на оборот. dMx/dz>0.

3. На участке, где q=const, Qy изменяется по линейному закону; Мх – по параболе.

Если q=const, то из (1) получаеться: Qy=-qz+c1 Подставляем (2):

dMx/dz=-qz+c1

Mx=-q*((z^2)/2)+c1*z+c2

Эти условия используются для проверки правильности построения эпюра Qy и Mx.

3. Растяжение и сжатие стержней

Если в конструкциях возникает только один внутренний силовой фактор, то такой случай нагружения называются про­стыми. К простому виду нагружения относится растяжение (сжатие) стержня, при котором в его поперечном сечении возникает единст­венный внутренний силовой фактор - продольная (нормальная) сила N.

Осевым растяжением (сжатием) стержня называется вид нагру­жения, при котором возникает только продольная сила N.

Величины внутренних сил находят с использованием метода сече­ний и принятого правила знаков.

Рассмотрим стержень растянутый силами, равномерно распределенными по торцам. Если нанести на поверхность стержня сетку, то после деформации (растяжения) линии останутся прямыми и взаимноперпендикулярными. Следовательно деформации и напряжения во всех сечениях будут одинаковыми и в сечении σ=const →

→ N= *A

σ=N/A – нормальное напряжение при растяжении и сжатии стержня.

Полученные результаты применимы и для сжатых стержней, при деформировании которых, в отличии от растянутых, продольная си­ла отрицательна.

Описанная кар­тина деформирования стержня соответствует гипотезе плоских сече­ний, впервые высказанной голландским ученым Д. Бернулли. Соглас­но этой гипотезе поперечные сечения стержня, плоские до деформа­ции, остаются плоскими и после деформации.

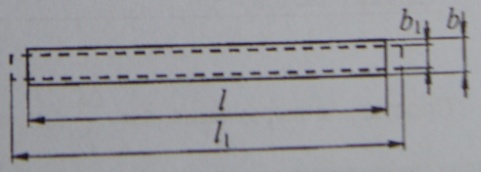
Как показывают опыты, при растяжении длина стержня увеличива­ется, а поперечные размеры уменьшаются (рис). При сжатии - наоборот, стержень становится короче, а поперечные размеры увели­чиваются.

∆L=L1-L- удлинение стержня

∆b=b1-b- изменение поперечного размера

Относительная продольная деформация ε и относительная поперечная деформация ε' вычисляются по формуле: ε=∆L/L; ε'= ∆b/b

Отношение относительной поперечной деформации ε' к относи­тельной продольной деформации ε, взятое по модулю, называется ко­эффициентом Пуассона: или |∆b/∆L|.

Величина v является постоянной для изотропного материала и опре­деляется экспериментально.

Значения v для различных материалов изменяются в пределах 0< V <0,5. 0,3 – сталь, 0,5 – резина, 0 – пробка.

В пределах малых удлинений, для многих материалов справедлив закон Гука:

σ=E*ε

Нормальные напряжения в поперечном сечении прямо пропорцио­нальны относительной продольной деформации.

Коэффициент пропорциональности Е в формуле называется модулем упругости (модулем Юнга). Величина Е является постоян­ной для любого изотропного материала, которая определяется опыт­ным путем и характеризует его жесткость, т.е. способность сопротив­ляться деформированию под действием продольных сил.

Подставляя выражения ε=∆L/L, σ=N/A получим: ∆L=NL/EA – удлинение стержня при растяжении и сжатии. Величина ЕА называется жесткостью стержня при растяжении- сжатии.

Коэффициенты Е и v являются основными характеристиками уп­ругости изотропного материала.