Строгий и нестрогий порядок
Отношение,
удовлетворяющее условиям рефлексивности,
транзитивности и антисимметричности,
также называют нестрогим,
или рефлексивным
порядком.
Если условие рефлексивности заменить
на условие антирефлексивности (тогда
свойство антисимметричности заменится
на асимметричность):

то
получим определение строгого,
или антирефлексивного
порядка.
Если  —
нестрогий порядок на множестве
—
нестрогий порядок на множестве 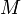 ,
то отношение
,
то отношение  ,
определяемое как:
,
определяемое как:

является
строгим порядком на
.
Обратно, если
—
строгий порядок, то отношение
,
определенное как

является нестрогим
порядком.
Бинарное
отношение  на множестве
на множестве  называется отношением
порядка,
или отношением
частичного порядка,
если имеют место
называется отношением
порядка,
или отношением
частичного порядка,
если имеют место
Рефлексивность: 
Транзитивность:  ;
;
Антисимметричность:  .
.
отношение
R
частичного порядка на множестве А
называется отношением линейного
порядка,если для любых элементов x,y
(принадл.)А верно хотя бы одно из
утверждений :(x,y)(принадл.)R
или (y,x)(принадл.)R
отношение
R
частичного порядка на множестве А
называется отношением полного
порядка,еслив любом подмножестве
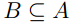 найдется наименьший элемент,то есть
такой элемент
найдется наименьший элемент,то есть
такой элемент
 ,что для любого
,что для любого
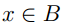 имеет место включение
имеет место включение
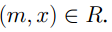

Множество X всех
допустимых действительных значений
аргументаx, при которых функция y
= f (x) определена,
называется областью
определения функции.
Множество Y всех
действительных значений y, которые
принимает функция,называется областью
значений функции.
Теперь можно дать
более точное определение функции:
правило(закон)
соответствия между множествами X и Y,
по которому для каждого элемента из
множества X можно найти один и только
один элемент из множества Y,
называется функцией.


