Виды бинарных отношений на множестве a

1)          Обратное отношение   .

2)          Дополнение                  .

3)          Тождественные              .

4)     Универсальные               .Композиция отношений

Пусть   -отношение из A в C ,   и   - отношение из         C в B, ,  тогда композицией  отношений   называется отношение

     .

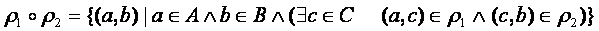Отношения обладают степенью и мощностью. Степень отношения - это количество элементов в каждом кортеже отношения (аналог количества столбцов в таблице). Мощность отношения - это мощность множества кортежей отношения (аналог количества строк в таблице).

Транзитивным замыканием  отношения  называется отношение, определяемое следующим образом: если в множестве  существует цепочка из  элементов, в которой между каждыми двумя соседними элементами выполняется отношение (, то говорят, что существует транзитивное замыкание .

• Транзитивным замыканием отношения R называется бинарное отношение R’ такое, что x R’ y тогда и только тогда, когда существует такая цепочка элементов из X:

• z₀ = x, z₁, z₂, ..., z_n = y,

• что между соседями в этой цепочке выполнено отношение R:

• z₀ Rz₁, z₁R z₂, ..., z_n-1 Rz_n.

. Св-ва бинарных отношений

1) Рефлексивность (если всякий элемент этого множества находится в отношении R с самим собой)

2) Антирефлексивность (все диагональные элементы матрицы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х)) .

3) Симметричность (для каждой пары элементов множества (a,b) выполнение отношения aRb влечёт выполнение отношения bRa) .

4) Антисимметричность (для каждой пары элементов множества a,b выполнение отношений aRb и bRa влечёт a = b, или, что то же самое, выполнение отношений aRb и bRa возможно только для равных a и b) .

5) Транзитивност ь (для любых трёх элементов множества a,b,c выполнение отношений aRb и bRc влечёт выполнение отношения aRc)

.

5) Полнота .

6) Асимметричность (эквивалентна одновременной антирефлексивности и антисимметричности отношения) .

Рефлексивное отношение в математике - это такое отношение, что любой элемент всегда соотносится с самим собой. Нерефлексивное отношение - это такое отношение, что никакой элемент не соотносится с самим собой.

Пусть на множестве X задано бинарное отношение R. Тогда R называется рефлексивным, если

Отношение R называется нерефлексивным (или иррефлексивным), если

Отношение называется антирефлексивным, если ни один элемент a ∈ M не находится в отношении R с самим собой

Пусть на множестве X определено бинарное отношение R. Тогда R называется симметричным, если

 Отношение R называется асимметричным, если оно не является симметричным.

 Отношение R называется антисимметричным, если

Транзитивное отношение в математике - это такое отношение, при котором если один элемент соотносится с вторым, а второй с третьим, то и первый элемент соотносится с третьим.

Пусть на множестве X задано бинарное отношение R. Тогда это отношение называется транзитивным, если

Если бинарное отношение R транзитивно, то его обратное R − 1 также транзитивно.

Пересечение двух транзитивных отношений также транзитивно. Это, вообще говоря, неверно для объединения.

Полное отношение в математике - это бинарное отношение, при котором любые два элемента соотносятся друг с другом некоторым образом.

Пусть на множестве X определено бинарное отношение R. Тогда R называется полным (или линейным), если

 Если R - отношение порядка, то оно называется полным (линейным) порядком, а множество Xназывается полностью упорядоченным.

Отношение ○ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.

Всякое отношение эквивалентности   во множестве A позволяет специальным образом различать элементы этого множества. Обозначим через C (a)множество всех элементов x из A, таких, что   Это множество является подмножеством A, которое называется классом эквивалентности a. Если   то в силу симметричности и транзитивности отношения   любой элемент x, эквивалентный a, эквивалентен и b. Если же b не эквивалентен a, то C (a) и C (b) не имеют общих элементов, потому что если   и  , то в силу симметричности   и  , и в силу транзитивности   что противоречит условию. Таким образом, отношением эквивалентности множество A разбивается на непересекающиеся классы эквивалентности, при котором каждый элемент A попадает в свой класс.

Как мы видели в приведенных выше примерах, равенство на множестве отрезков является отношением эквивалентности и задает его разбиение на классы эквивалентности. Каждый такой класс содержит отрезки заданной длины.

Пусть дано множество X, и на нём задано бинарное отношение ˜.. Тогда ˜ называется отношением эквивалентности, если оно

 рефлексивно, то есть

 симметрично, то есть

 транзитивно, то есть

Подмножество элементов эквивалентных данному называется его классом эквивалентности. Пишут:

Пусть   Тогда либо   либо [a] = [b]. Таким образом отношение эквивалентности порождает разбиение множества на непересекающиеся классы эквивалентности. Семейство таких классов образует множество, называемое фактор-множеством и обозначаемое X / ˜.

если R-отношение эквивалентности на множестве М,то множество классов эквивалентных по R элементов называется фактор-множеством M/R ножества М по отношению R