4. Двухфакторный анализ без повторений
В тех случаях, когда в каждом классе дисперсионного комплекса имеется лишь по одному наблюдению, применяется так называемый двухфакторный дисперсионный анализ без повторности.
Пример. Необходимо методом дисперсионного анализа оценить влияние профиля цеха и особенностей производственного процесса на заболеваемость рабочих острым и хроническим гастритом. Исходные данные представлены в таблице (Рисунок 6):
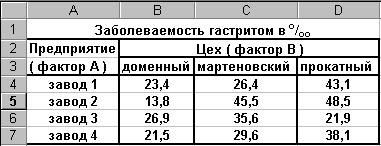
Рисунок 6
Согласно таблице фактор А имеет 4 уровня (заводы 1-4), а фактор В - 3 уровня (доменный, мартеновский и прокатный цеха). В каждой группе имеется только по одному наблюдению.
Для решения задачи в MS Excel:
1.Сформируйте таблицу с исходными данными (рисунок 6).
2.Выполните команду Анализ данных из меню Сервис.
3.В соответствии с условиями задачи выберите в появившемся диалоговом окне метод "Двухфакторный дисперсионный анализ без повторений" и нажмите кнопку [OK].
4.В окне "Двухфакторный дисперсионный анализ без повторений" установите для входных данных следующие параметры:
входной интервал равен $B$4:$D$7,
входной диапазон не содержит метки,
альфа (уровень значимости равен 0,05),
5.Для параметров вывода установите переключатель в положение "Новый рабочий лист".
6.После завершения настройки параметров нажмите кнопку [OK].
Результаты дисперсионного анализа будут представлены на новом листе и состоять из двух таблиц. В первой таблице для каждой строки и каждого столбца исходной таблицы приведены числовые параметры: количество чисел, сумма, среднее и дисперсия.
Вторая часть результатов представлена на рисунку 7.
Рисунок
7
Таким образом, суммы квадратов, обусловленные влиянием фактора А (источник вариации – "Строки") и фактора В (источник вариации – "Столбцы"), равны 102,0 и 601,5, соответственно, а остаточная сумма квадратов ("Погрешность") равна 597,0. Факторные дисперсии равны 34,0 (фактор А) и 300,8 (фактор В), а остаточная дисперсия - 99,5.
Основной вывод из полученных результатов заключается в следующем:
Нет оснований отвергать нулевую гипотезу об отсутствии влияния каждого из рассмотренных факторов на заболеваемость рабочих гастритом, т.к. для обоих факторов выполняется неравенство F<Fкр. Принятие нулевой гипотезы подтверждается и величинами значимостей, равными 0,797 для фактора А и 0,124 для фактора В.
Итак, заболеваемость рабочих острым и хроническим гастритом не зависит от профиля цеха и номера завода. Поэтому нет смысла вычислять силу влияния факторов.
5.Двухфакторный анализ с повторяющимися данными
Двухфакторный дисперсионный анализ с повторениями используется в том случае, когда в каждой группе данных имеется более одной выборkи. Он позволяет учесть как влияние отдельных факторов, так и их совместное действие на результативный признак.
Примечание: Проведение двухфакторного дисперсионного анализа с повторениями в Excel имеет ограничение – все выборки должны быть одинаковыми. Поскольку каждая строка представляет повторение данных, то каждая выборка должна содержать одно и тоже количество строк.
Рассмотрим пример применения двухфакторного дисперсионного анализа с повторениями.
Исследуем влияние формы токсического зоба (фактор А), имеющего два уровня (узловая и диффузная формы) и дозы мерказолила (фактор В), имеющего три уровня (20 мг/сутки, 25 мг/сутки, 30 мг/сутки) и на длительность устранения тиреотоксикоза. Статистический комплекс представлен в Excel-таблице (Рисунок 8). Числовые данные определяют длительность выхода (в сутках) больных из токсикоза для различных комбинаций уровней двух факторов (в каждой из 6 подгрупп имеется по 3 наблюдения).
Для выполнения расчетов двухфакторного комплекса:
1.Сформируйте таблицу с исходными данными (Рисунок 8).