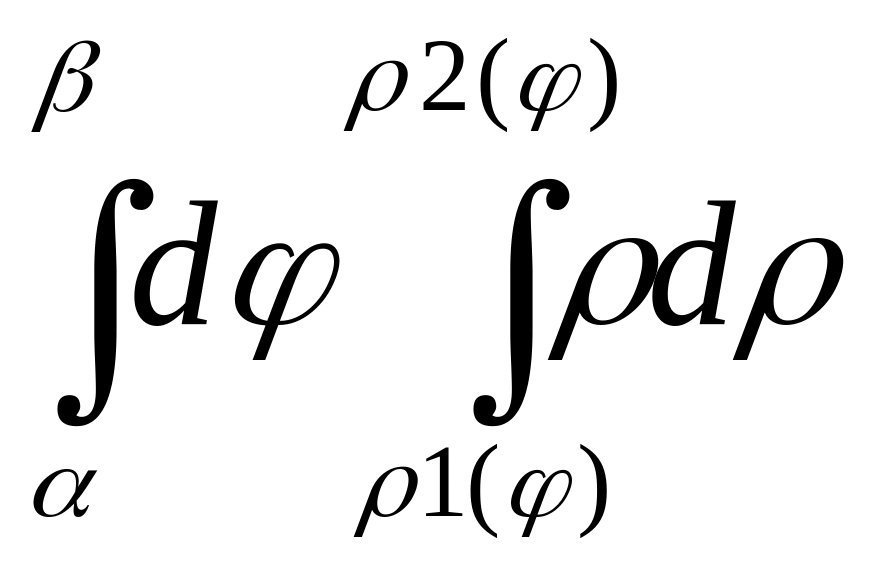- •1. Определение первообразной, теорема о множестве первообразных. Неопределенный интеграл. Основные свойства (линейность, интеграл от производной функции).
- •2. Неопределенный интеграл. Замена переменной в интеграле. Интегрирование по частям.
- •3. Общая схема интегрирования рациональных функций.
- •9. Определенный интеграл: определение, свойства линейности
- •10. Определенный интеграл: определение, теорема о среднем, ее геометрический смысл.
- •11. Теорема о дифференцировании интеграла по верхнему пределу. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
- •12. Вычисление площадей плоских фигур в прямоугольных и полярных координатах с помощью определенного интеграла.
- •13.Определение длины кривой. Вычисление длины кусочно-гладкой кривой.
- •18. Несобственные интегралы: признаки сравнения.
- •19. 0Пределение двойного интеграла, его геометрический и механический смысл. Свойства линейности и аддитивности; сведение двойного интеграла к повторному.
- •20. Двойной интеграл: интегрирование неравенств, оценка интеграла, теорема о среднем.
- •21. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •22. Геометрические и механические приложения двойного интеграла.
- •23. Определение тройного интеграла. Сведение тройного интеграла к повторному.
- •24.Тройной интеграл в цилиндрических и сферических координатах.
- •25.Определение криволинейного интеграла по длине дуги, его геометрический и механический смысл, вычисление.
- •26. Определение и основные свойства криволинейного интеграла по координатам, вычисление.
- •27. Работа силового поля. Физический смысл интеграла по координатам.
- •28.Теорема Грина.
- •29. Условие независимости криволинейного интеграла по координатам от выбора пути интегрирования (на плоскости).
- •30. Вычисление площади гладкой поверхности.
- •31 .Определение интеграла первого рода по поверхности. Формулы для его вычисления.
- •32.Производная по направлению и градиент скалярного поля. Геометрический смысл градиента, его свойства.
- •33. Определение и свойства интегралов второго рода по поверхности, вычисление.
- •34. Поток векторного поля, дивергенция. Теорема Гаусса-Острогр.
- •36. Циркуляция векторного поля, ротор. Теорема Стокса. Формула Грина как частный случай теоремы Стокса.
18. Несобственные интегралы: признаки сравнения.
1 признак сравнения: если х ≥ а и f1(x) и f2(x)—непрерывны для любого Х принадлежащего [ a , +∞ ] и выполняется условие 0 ≤ f1(x) ≤ f2(x), то
1)
![]() f2(x)
dx
–сходится
f1(x)
dx
–сходится. 2)
f1(x)
dx
–расходится
f2(x)
dx
–расходится. 2
признак сравнения:
если х ≥ а и f1(x)
и f2(x)
≥ 0, то существует
f2(x)
dx
–сходится
f1(x)
dx
–сходится. 2)
f1(x)
dx
–расходится
f2(x)
dx
–расходится. 2
признак сравнения:
если х ≥ а и f1(x)
и f2(x)
≥ 0, то существует
Lim ( f1(x)) / ( f2(x)) = K ( при Х +∞ ) , то оба интеграла сходятся и расходятся одновременно. Следствие: если f(x) ≤ M / Xp , то P > 1, f(x) ≥ M / Xp , то P ≤ 1
Если сходится интеграл от модуля функции и интеграл от функции, то это абсолютно сходящийся интеграл. Если интеграл от модуля расходится, а от функции—сходится, то это условно-сходящийся интеграл.
19. 0Пределение двойного интеграла, его геометрический и механический смысл. Свойства линейности и аддитивности; сведение двойного интеграла к повторному.
Двойным интегралом от функции f ( x, y ) по области Д называется ∫∫ f ( x, y ) dxdy = Lim ∑ f ( xi , yi )ΔSi ( при dt 0 ). ΔSi –интегральная сумма разбиений. Геометрический смысл: двойной интеграл есть объем цилиндрического тела, ограниченного сверху поверхностью Z = f ( x, y ). Линейность:
∫∫ ( f ( x, y) ± g ( x, y)) dxdy = ∫∫ ( f ( x, y) dxdy ± ∫∫ ( g ( x, y) dxdy , а так же:
∫∫ λ f
( x,
y)
dxdy
= λ ∫∫ ( f
( x,
y)
dxdy
. Аддитивность:
![]() f
( x,
y)
dxdy
=
f
( x,
y)
dxdy
=
![]() f
( x, y) dxdy +
f
( x, y) dxdy +
![]() f
( x, y) dxdy.
f
( x, y) dxdy.
Сведение двойного
интеграла к повторному: если f
непрерывна в области Д, то
![]() f
( x,
y)
dxdy
=
f
( x,
y)
dxdy
=
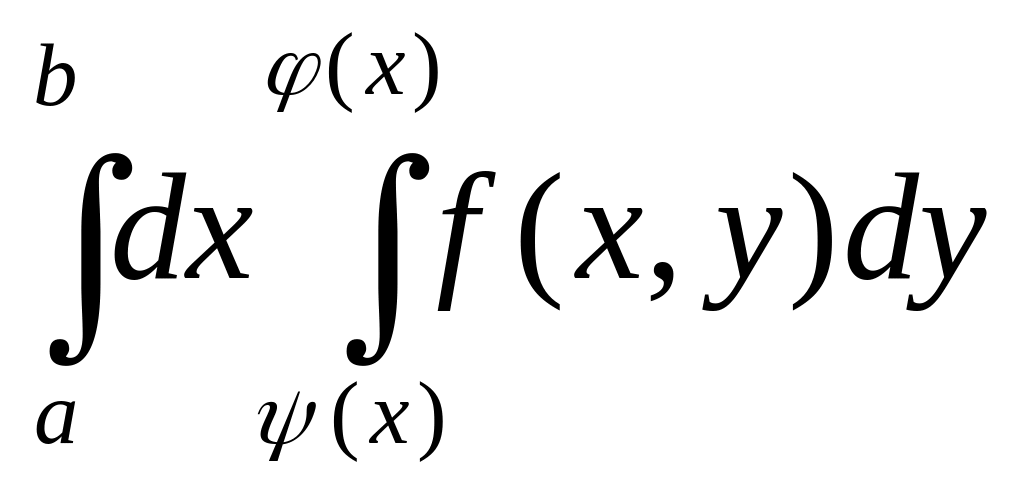 .
В правой части формулы стоит повторный
интеграл. Если область Д не является
простой, то ее нужно разбить на простые
части. Если область интегрирования
задается прямоугольником, то пределы
интегрирования—константы. Если область
дифференцирования—что-то похожее на
эллипс, то можно выбирать пределы
интегрирования по любым осям.
.
В правой части формулы стоит повторный
интеграл. Если область Д не является
простой, то ее нужно разбить на простые
части. Если область интегрирования
задается прямоугольником, то пределы
интегрирования—константы. Если область
дифференцирования—что-то похожее на
эллипс, то можно выбирать пределы
интегрирования по любым осям.
20. Двойной интеграл: интегрирование неравенств, оценка интеграла, теорема о среднем.
Теорема о среднем: если f(x, y )—непрерывна в области Д, то найдутся x, y принадлежащие Д, такие, что f ( x, y) dS = f(x, y)*SД. доказательство: так как f(x, y )—непрерывна в области Д, то она принимает все свои значения, то есть m ≤ ( ∫∫f(x, y ) dS ) / SД ≤ М f ( x, y) dS = f(x, y)*SД.
21. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
При переходе к
криволинейным координатам считают: U
= U(
x,
y
), V
= V(
x,
y
), тогда X
= X(
u,
v
), Y
= Y(
u,
v
). Также вводится Якобиан. Он считается
подобно определителю J
=
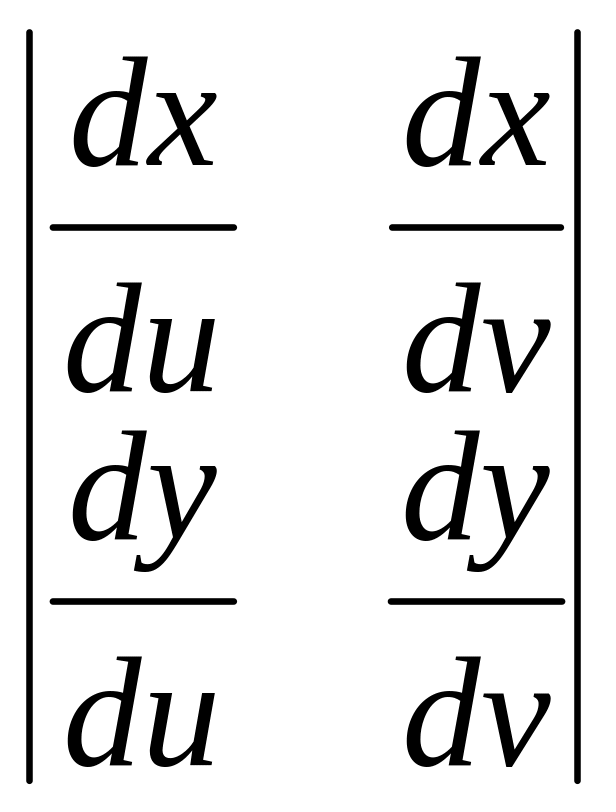 , тогда dS
= | J
| dudv.
Якобиан в любой точке М, области Д, есть
коэффициент изменения площади при
деформации области Д. Исходя из этого:
, тогда dS
= | J
| dudv.
Якобиан в любой точке М, области Д, есть
коэффициент изменения площади при
деформации области Д. Исходя из этого:
S(Д)
=
![]() .
В полярных координатах: X
= ρcosφ,
Y
=ρsinφ,
тогда якобиан имеет вид: J
=
.
В полярных координатах: X
= ρcosφ,
Y
=ρsinφ,
тогда якобиан имеет вид: J
=
![]() . Он будет равен: ρ.
. Он будет равен: ρ.
Тогда
f
( x,
y)
dxdy
=
f
( ρcosφ,
ρsinφ
) ρdρdφ.
Или
f
( ρ,
φ ) ρdρdφ
=