18. Несобственные интегралы. Интеграл в смысле главного значения
К
Н. и. относятся интегралы в смысле
главного значения. Пусть функция f
определена на открытом множестве 
,
кроме, быть может, точки 
,
и пусть для любого 
функция
f интегрируема (по Риману или по Лебегу)
на множестве 
есть 
-окрестность
точки х. Тогда если существует
предел 
то его наз. интегралом в смысле главного значения и обозначают
Если интеграл
существует
как Н. и., то он существует и в смысле
главного значения. Обратное, вообще
говоря, неверно. Напр., Н. и.
расходится,
а 
Аналогично определяют интегралы в смысле главного значения в бесконечно удаленной точке.
19. Двойной интеграл. Вычисление двойного интеграла
Пусть
обл-ть D задана неравенствами
т.е. изображается прямоугольником.
Тогда двойной интеграл вычисляется по
одной из формул
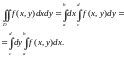В
1-й формуле сначала вычисляется внутренний
интеграл
.
В процессе этого интегрирования x
рассм-ся как постоянная величина. Но
результат интегрирования рассм-ся как
ф-ция от х, и второе интегрирование (в
пределах от a до b) выполняется по
аргументу x. Во 2-й формуле порядок
действий обратный.
1.
Если контур области D встречается со
всякой пересекающей его вертикальной
прямой не более чем в двух точках
(М1,М2), то обл-ть D задаётся неравенствами
.
[a, b – крайние абсциссы обл-ти, φ1(x), φ2(x)
– ф-ции, выражающие ординаты нижней и
верхней граничных линий AM1B1, AM2B2]. В этом
случае двойной интеграл вычисляется
по формуле (если ф-ция f(x,y) непрерывна
на элементарном множестве D):
(1) 2. Если контур области встречается
не более чем в двух точках со всякой
пересекающей его горизонтальной прямой,
имеем аналогично (при обозначениях
чертежа 2).
(2) 3. Если область интегрирования не
является элементарной, т.е. не подходит
ни под первый, ни под второй случай, то
область D разбивают на несколько частей
(D1, D2, D3 на чертеже 3) так, чтобы к кажой
части была применима формула (1) или
(2).
20. Двойной интеграл. Замена переменных в двойном интеграле
Замена переменных в двойном интеграле описывается формулой
где
выражение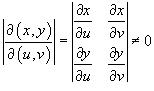 
представляет
собой так называемый якобиан преобразования 
,
а S − образ области
интегрирования R, который можно найти
с помощью подстановки 
в
определение области R. Отметим, что
в приведенной выше формуле 
означает
абсолютное значение соответствующего
определителя.
Предполагая,
что преобразование координат
является
взаимно-однозначным, обратное соотношение
описывается якобианом
при условии, что знаменатель нигде не равен 0. Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:
Найти
образ S в новой системе координат 
для
исходной области интегрирования R;
Вычислить
якобиан преобразования
и
записать дифференциал в новых переменных
;
Заменить
в подынтегральном выражении исходные
переменные x и y, выполнив,
соответственно, подстановки 
и 
.
21. Тройной интеграл. Вычисление тройного интеграла
Пусть
ф-ция u=f(x,y,z) непрерывна внутри замкнутой
пространственной области V и на её
границе. Разобьём область V сеткой
поверхностей на части, которые пронумеруем
индексами i, j, k:
– длины сторон при
Т.е. можно утверждать, что Vчаст→V.
Выберем в каждой части произвольную
точку (ζi, ηi, θi). Составим интегральную
сумму
для ф-ции f(x,y,z) по обл-ти V. Если предел
интегральной суммы существует при
неограниченном увеличении числа n таким
образом, что каждая «элементарная
область» Vi стягивается в точку, т.е.
диаметр области стремится к нулю, т.е.
di→0), то его называют тройным интегралом
от ф-ции u=f(x,y,z) по области V и обозначают
Вычисление.
Пусть областью интегрирования
является тело, ограниченное снизу
поверхностью z=z1(x,y), сверху – поверхностью
z=z2(x,y), причем f(x,y) и g(x,y) – непрерывные
ф-ции в замкнутой области D, являющейся
проекцией тела на плоскость Oxy. Будем
считать область V – правильной в
направлении оси Oz: любая прямая
параллельная оси Oz, пересекает границу
области не более чем в двух точках.
Тогда для любой непрерывной в области
V ф-ции f(x,y,z) имеет место формула
.
В процессе вычисления интеграла
величины
x, y являются постоянными. Результат
вычисления рассматривается как ф-ция
аргументов x,y. После того как интегрирование
по переменной z выполнено, правая часть
превращается в двойной интеграл. Поэтому
в итоге тройной интеграл сводится к
повторному:
