- •Аксиомы статики
- •Связи и их реакции
- •Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.
- •Момент силы относительно центра
- •Момент силы относительно оси. Аналитический и геометрический способы.
- •Пара сил. Теорема о сумме моментов сил пары относительно произв. Центра.
- •Теоремы о парах.
- •Лемма о параллельном переносе силы (лемма Пуансо)
- •Основная теорема статики
- •Условия равновесия твердого тела под действием произвольной плоской и пространственной системы сил.
- •Законы трения скольжения. Равновесие при наличии трения скольжения.
- •Трение качения. Равновесие при наличии трения качения.
- •Определение первого и второго статических инвариантов. Частные случаи приведения произвольной системы сил к центру.
- •Теорема Вариньона в векторной и скалярной формах
- •Центр тяжести. Основные методы.
- •Метод интегрирования.
- •Метод симметрии.
- •Метод разбиения.
- •Методы отрицательных весов, объемов и площадей.
- •Способы задания движения точки
- •Определение скорости и ускорения точки при векторном способе задания движения.
- •Координатном
- •Естественном
- •Поступательное движение тела. Теорема о траекториях, скоростях, ускорениях точек тела. Уравнение поступательного движения.
- •Вращательное движения твердого тела. Понятие угловой скорости и ускорения.
- •Определение скоростей и ускорений вращающегося предмета. Формула Эйлера.
- •Понятие сложного, абсолютного, относительного и переносного движений.
- •Теорема о сложении скоростей при сложном движении.
- •Теорема о сложении ускорений при сложном движении. (т. Кориолиса)
- •Ускорение Кориолиса. Способы вычисления.
- •Плоскопараллельное движение.
- •Теорема о скоростях точек тела при его плоском движении и следствия о проекциях скоростей двух его точек на ось, проходящую через 2 эти точки.
- •Мгновенный центр скоростей. Способы нахождения.
- •Теорема об ускорениях точек тела при плоском движении и следствия о проекциях ускорений двух его точек на ось, проходящую через 2 эти точки.
Теорема о сложении скоростей при сложном движении.
Абсолютная скорость точки M определяется как геометрическая сумма скоростей переносного и относительного движений
νa = νe + νr .
Смысл и значение теоремы о скоростях заключается в том, что относительную и переносную скорости можно определять независимо друг от друга. Абсолютная скорость определяется как геометрическая сумма относительной и переносной скоростей.
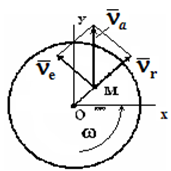
Относительное движение точки M происходит вдоль радиуса в соответствии с уравнением OM = s(t) . Следовательно, относительная скорость точки M будет равна производной от OM по времени νr = dOM / dt .
Поскольку относительное движение происходит по прямой, относительная скорость направлена вдоль этой прямой.
Переносная скорость точки M определится выражением
νe = ω ⊗ OM или νe = ω ⋅ OM, т.к. ω ⊥ νe
и направлена перпендикулярно OM в сторону вращения диска.
Угол между νe и νr равен, в данном случае, 90° и модуль абсолютного ускорения определится формулой
![]()
Теорема о сложении ускорений при сложном движении. (т. Кориолиса)
Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений
aa = ar + ae + aC .
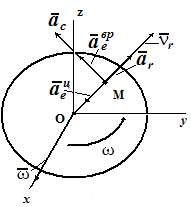
Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение ar направлено вдоль этой прямой и определяется выражением
![]()
Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением
ae = aeвр + aeцс ,
где aeвр= ε⋅ OM - вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;
aeцс= ω2⋅ OM - центростремительное ускорение точки M, направленное к центру диска.
Ускорение Кориолиса. Способы вычисления.
Ускорение Кориолиса или поворотное ускорение определяется по формуле
aC = 2 ωe * νr ,
где ωe - переносная угловая скорость,
νr - относительная скорость точки.
Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.
Величина ускорения Кориолиса определяется выражением
aC = 2 ωe νr sinα ,
где α – угол между векторами ωe и νr .
Ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.
Плоскопараллельное движение.
Плоско-параллельным движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости. То есть точки М1 и М2 тела А, например, двигаются в плоскостях Q1 и Q2, соответственно параллельных плоскости Q. Если в первоначальной момент отрезок М1М2 перпендикулярен плоскостям Q, Q1, Q2, то и при последующем движении тела он остается параллельным своему первоначальному положению и перпендикулярным к этим плоскостям, т.е. движется поступательно. Следовательно, скорости и ускорения всех точек тела, лежащих на отрезке М1М2, равны и одинаково направлены.
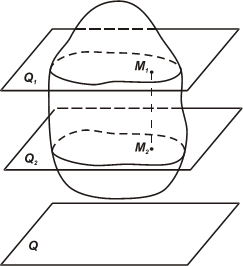
Это позволяет свести изучение движение отрезка М1М2 к изучению движения точки М1 или М2 вместе с соответствующим сечением тела в плоскости.
Положение фигуры в плоскости вполне определяется положением в этой плоскости какого-нибудь отрезка, например АВ, скрепленного с фигурой. Положение отрезка будет вполне определено, если будет известно положение какой-либо точки, например А (полюс), и угла наклона (φ) отрезка к выбранной оси.
Тогда закон движения фигуры в плоскости может быть записан в виде
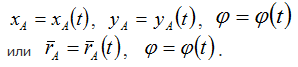
Закон вращательного движения не зависит от выбора полюса.