- •Аксиомы статики
- •Связи и их реакции
- •Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.
- •Момент силы относительно центра
- •Момент силы относительно оси. Аналитический и геометрический способы.
- •Пара сил. Теорема о сумме моментов сил пары относительно произв. Центра.
- •Теоремы о парах.
- •Лемма о параллельном переносе силы (лемма Пуансо)
- •Основная теорема статики
- •Условия равновесия твердого тела под действием произвольной плоской и пространственной системы сил.
- •Законы трения скольжения. Равновесие при наличии трения скольжения.
- •Трение качения. Равновесие при наличии трения качения.
- •Определение первого и второго статических инвариантов. Частные случаи приведения произвольной системы сил к центру.
- •Теорема Вариньона в векторной и скалярной формах
- •Центр тяжести. Основные методы.
- •Метод интегрирования.
- •Метод симметрии.
- •Метод разбиения.
- •Методы отрицательных весов, объемов и площадей.
- •Способы задания движения точки
- •Определение скорости и ускорения точки при векторном способе задания движения.
- •Координатном
- •Естественном
- •Поступательное движение тела. Теорема о траекториях, скоростях, ускорениях точек тела. Уравнение поступательного движения.
- •Вращательное движения твердого тела. Понятие угловой скорости и ускорения.
- •Определение скоростей и ускорений вращающегося предмета. Формула Эйлера.
- •Понятие сложного, абсолютного, относительного и переносного движений.
- •Теорема о сложении скоростей при сложном движении.
- •Теорема о сложении ускорений при сложном движении. (т. Кориолиса)
- •Ускорение Кориолиса. Способы вычисления.
- •Плоскопараллельное движение.
- •Теорема о скоростях точек тела при его плоском движении и следствия о проекциях скоростей двух его точек на ось, проходящую через 2 эти точки.
- •Мгновенный центр скоростей. Способы нахождения.
- •Теорема об ускорениях точек тела при плоском движении и следствия о проекциях ускорений двух его точек на ось, проходящую через 2 эти точки.
Центр тяжести. Основные методы.
Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела
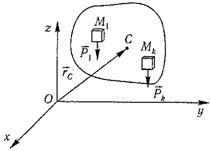
Радиус-вектор этой точки
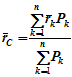
Метод интегрирования.
Выражаем координаты центра тяжести неоднородного тела следующим образом:
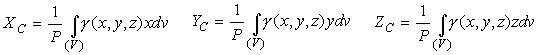
Для однородных тел (центры тяжести объема, поверхности, площади и линии) эти координаты мы находим по формулам:
|
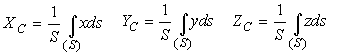
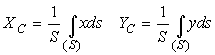
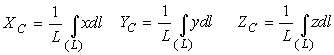
dv, ds, dl - элементарные объемы, площади и отрезки, x,y,z - координаты этих элементарных объемов, площадей и отрезков, а P для неоднородного тела вычисляется как
|
Метод симметрии.
Метод применяется только для однородных
тел. Опуская несложные доказательства,
сформулируем три правила метода. 
1. Если тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
2. Если тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3. Если тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
Используя правила, определим положение центра тяжести однородного цилиндра высотой H.
Рассечем цилиндр по диаметру плоскостью П1, которая является первой плоскостью симметрии цилиндра (рис. 43). Рассекая цилиндр по другому диаметру второй плоскостью симметрии П2, найдем ось симметрии AA цилиндра, являющуюся линией пересечения двух плоскостей симметрии и совпадающую с осью цилиндра. Наконец, рассекая цилиндр пополам плоскостью П3, перпендикулярной оси цилиндра, найдем центр симметрии C, находящийся в точке пересечения плоскости симметрии П3 с осью симметрии AA. Таким образом, центр тяжести однородного цилиндра находится на оси цилиндра на высоте H/2 от основания (рис. 43).
Метод разбиения.
Он применяется, когда однородное тело
можно разбить на части, положения центров
тяжести которых известны или легко
определяются. В неоднородном теле эти
части должны иметь еще и одинаковый
удельный вес во всех их точках. После
разбиения положение центра тяжести
всего тела находят, используя дискретные
формулы для определения координат
центра тяжести. 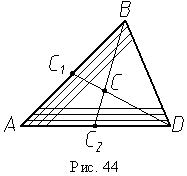
Применим метод для плоского однородного треугольника. Разобьем треугольник ABD на узкие полоски, параллельные стороне AD (рис. 44). Центры тяжести отрезков линий, за которые в пределе приняты полоски, будут лежать на медиане BC1, там же должен лежать и центр тяжести всего треугольника. Аналогичные результаты получатся для медианы DC2, когда полоски параллельны стороне AB треугольника. Следовательно, точка C пересечения медиан будет центром тяжести всего треугольника. Причем из геометрии известно, что CC1 = BC1 / 3 , а CC2 = DC2 / 3.
Методы отрицательных весов, объемов и площадей.

Методы являются частными случаями метода разбиений и применяются для тел с полостями (отверстия, вырезы и т.д.). В них используется идея метода разбиений, но при нахождении центра тяжести по формулам веса, объемы или площади полостей берут со знаком "-".
Применим метод отрицательных площадей для нахождения координат центра тяжести однородного диска радиуса R с круглым отверстием радиуса r, когда R = 2r (рис. 46). Принимаем за ось C1X ось симметрии полученной плоской фигуры, где C1 - начало координат, совпадающее с центром тяжести диска без отверстия. Точкой C2 обозначен центр тяжести отверстия. По правилам симметрии центр тяжести фигуры находится на оси C1X, поэтому YC = 0. Координату XC определяем по первой формуле (14), присваивая в ней знак "-" площади отверстия s2:
![]()
Здесь
![]()
Тогда

Анализ результата показывает, что центр тяжести C диска с отверстием смещен от отверстия в сторону тяжелой части плоской фигуры.
КИНЕМАТИКА