37)Неопределенные интегралы простецших элементарных функций:

38)Формула интегрирования по частям: .То есть,подынтегральное выражение f(x)dx представляем в виде произведения функции u(x) на d(v(x))- дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования)и d(u(x))-дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности .Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.В качестве примера найдем множество первообразных функции логарифма.

39)ЗАДАЧИ,ПРИВОДЯЩИЕ К ПОНЯТИЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА:Задача о пройденном пути:Требуется найти путь, пройденный движущейся по прямой точкой за отрезок времени ,если известен закон изменения мгновенной скорости v=v(t).Разобьем отрезок моментами времени (точками)  на n отрезков времени (частичных отрезков)и положим Наибольшую из этих  разностей обозначим через λ:  .Если эти отрезки достаточно малы,то без большой  ошибки движение на каждом из них можно считать равномерным,что дает для пути приближенное выражение где -одна из точек сегмента . Эта сумма    тем точнее выражает искомый путь s,чем  меньше каждый из временных отрезков  , k = 1, 2, ..., n.Поэтому за путь s, пройденный точкой в течение промежутка времени   со скоростью v = v (t), естественно принять предел указанной суммы при λ→0:       (1)  Задача о площади криволинейной трапеции: Пусть требуется найти площадь плоской фигуры   (рис.), 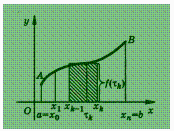  ограниченной графиком функции у = f (х), непрерывной и  неотрицательной на отрезке [a ; b], и отрезками прямых  .Эта фигура  называется криволинейной трапецией. Разобьем [a ; b] точками  на n частичных отрезков и положим .Наибольшую из этих разностей обозначим через λ: .На каждом частичном отрезке  , = l, 2, ...,n,  выберем произвольную точку  . Произведение     даст площадь  прямоугольника, имеющего основание   и высоту  , а сумма   -приближенно площадь S криволинейной трапеции aABb.  Отсюда, как и в предыдущей задаче,     

40)Понятие интегральной суммы,интеграл Римана:Геометрический смысл интеграла Римана.Интегра́л Ри́мана-одно из важнейших понятий математического анализа.Введён Бернхардом Риманом в 1854,и является одной из первых формализаций понятия интеграла.Неформальное геометрическое описание:Риман формализовал понятие интеграла,разработанное Ньютоном и Лейбницем, как площади подграфика(фигуры,заключенной между графиком функции и осью абсцисс).Для этого он рассмотрел фигуры,состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка(см. рисунок).Если при «размельчении» разбиения существует предел,к которому сходятся площади таких фигур(интегральные суммы),этот предел называется интегралом Римана функции на отрезке.Определения:Через интегральные суммы.Пусть на отрезке [a,b] определена вещественнозначная функция f. Рассмотрим разбиение отрезка  -конечное множество попарно различных точек отрезка.Это разбиение делит отрезок [a,b] на n отрезков  .Длина наибольшего из отрезков d=max(Δxi), где Δxi = xi − xi _{− 1},называется диаметром разбиения.Отметим на каждом отрезке разбиения по точке  Интегральной суммой называется выражение  .Если при стремлении диаметра разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора  , то это число называется интегралом функции f на отрезке[a,b], т.е.  В этом случае,сама функция f называется интегрируемой (по Риману) на[a,b]; в противном случае fявляется неинтегрируемой(по Риману) на отрезке [a,b].Через суммы Дарбу.Пусть на отрезке[a,b] определена вещественнозначная функция f. Рассмотрим произвольное разбиение отрезка  .Верхней суммой Дарбу для Δ называется число Соответстенно, нижней суммой Дарбу для Δ называется Функция называется интегрируемой по Риману, если существует вещественное число В этом случае, по определению Свойства:Если функция F является первообразной функции f, то интеграл функции f на отрезке [a,b] может быть вычислен по формуле Ньютона-Лейбница: он равен F(b)-F(a).Непрерывная на отрезке функция интегрируема по Риману.Ограничение: Если функция f интегрируема на отрезке [a,b], то она интегрируема и на меньшем отрезке [a₁,b₁], где  .Если функция интегрируема на отрезке [a,b] и на отрезке [b,c], то она интегрируема и на отрезке [a,c] и  .Линейность: Если функции f и g интегрируемы, и  , то функция αf + βg тоже интегрируема, и Предел: Если интегрируемые функции fi равномерно сходятся на отрезке [a,b] к функции f, то f интегрируема, и

41) Верхние и нижние суммы Дарбу.Суммы Дарбу:Пусть функция f (x) ограничена на отрезке [a, b] и τ – разбиение этого отрезка точками a = x ₀ < x ₁ < … < x _{i - 1} < x _i < … < x _n = b.Обозначим через m _i и M _i соответственно точную нижнюю и точную верхнюю грани этой функции на отрезке [ x _{i - 1}, x _i] и составим следующие суммы: ,  .Эти суммы называются соответственно верхней и нижней суммами Дарбу функции f (x)для данного τ – разбиения отрезка [a, b]. Из определения нижней и верхней граней следует, что m_i ≤ f ( ξ_i ) ≤ M_i при  вследствие чего имеем т. е. любая интегральная сумма и суммы Дарбу для данного разбиения связаны неравенствами s ≤ σ ≤ S. Суммы Дарбу имеют простой геометрический смысл. Рассмотрим неотрицательную непрерывную функцию f (x) на [a, b] и криволинейную трапецию, т. е. фигуру, ограниченную графиком функции f (x), двумя вертикальными прямыми, проведенными через точки a и b оси Ох, и осью Ох. Поскольку функция f (x) непрерывна на [a, b], она непрерывна и на [x_{i - 1}, x _i]. По второй теореме Вейерштрасса функция f(x) достигает на [x _{i - 1}, x _i] свои точные грани, и, следовательно, m _i иM _i — соответственно наименьшее и наибольшее значения функции на этом отрезке. Поэтому сумма S равна площади заштрихованной на ступенчатой фигуры, «описанной» около криволинейной трапеции, а сумма s равна площади ступенчатой фигуры, «вписанной» в данную криволинейную трапецию.Следует особо отметить, что суммы Дарбу зависят только от разбиения отрезка [a, b], в то время как интегральная сумма σ зависит еще и от выбора точек ξ _i на частичных отрезках [ x _{i - 1}, x_i ]. При фиксированном разбиении отрезка [a, b] суммы s и S – некоторые числа, а сумма σ – переменная величина, так как точки ξ _i произвольны.

42)Интегрируемость непрерывных функций:Если функция f(x)непрерывна на отрезке[a b],то она интегрируема на нем.    Доказательство.Так как функция f(x) непрерывна на отрезке [a,b],то по теореме Кантора она равномерно непрерывна на нем.Выберем произвольное как угодно малое ε>0.Согласно следствию из теоремы Кантора для положительного числа ε /(b - a) найдется δ > 0 такое, что при разбиении отрезка [a, b] на частичные отрезки [x _{i - 1}, x_i], длина которых Δ x_i < δ, все колебания ω_i меньше ε /(b - a). Отсюда при λ < δ.Следовательно, для непрерывной на отрезке [a, b] функции f (x) выполнено достаточное условие интегрируемости, а из него вытекает существование определенного интеграла.

43)Свойства определённых интегралов:1)Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции у=f(x),осью абсцисс,и прямыми х=а,х=b.Ниже приведена программа для построения криволинейной трапеции в пакете MAPLE.1)Если нижний и верхний пределы интегрирования поменять местами, то значение определённого интеграла изменится на противоположное

Доказательство: .2)Если промежуток интегрирования стянут в точку, фигура под кривой стягивается в отрезок, площадь которого равна нулю 2.Постоянный множитель можно выносить за знак интеграла где С — некоторое число.    Доказательство: 3)Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: Это свойство остается справедливым для любого конечного числа слагаемых.    Доказательство. 4)Если промежуток интегрирования разбит на части, то интеграл по всему отрезку равен сумме интегралов по каждой части.  Доказательство.Пусть а<с<b и функция f(x) неотрицательна на [a,b].Согласно геометрическому свойству определенного интеграла  ,   есть площади соответствующих криволинейных трапеций. Тогда при сделанных предположениях имеем равенство между площадями S = S ₁ + S ₂.5)Если на отрезке [a, b], где а < b, имеет место неравенство 0 ≤ f (x) ≤ g (x), то Обе части неравенства можно проинтегрировать, при этом смысл неравенства остаётся прежним.    Доказательство. Пусть фиксированы разбиение отрезка [a, b] и выбор точек x ₁, x ₂,…, x _n на каждом из отрезков разбиения. Тогда из неравенства f (x) ≤ g (x) вытекает аналогичное неравенство для интегральных сумм: .Переходя к пределу при max Δ x_i → 0, получим рассматриваемое неравенство для интегралов.    Следствие. Пусть на отрезке [a, b] где а < b, имеют место неравенства m ≤ f (x) ≤ M, где m и М — некоторые числа. Тогда Теорема о среднем. Если функция y = f (x) непрерывна на отрезке [a, b], где а < b, то найдется такое значение c Î [a, b], что По свойству функции, непрерывной на отрезке, для произвольного значения х Î [a, b] вверны неравенства m ≤ f(x) ≤M, где m и М — наименьшее и наибольшее значения функции на [a, b]. Тогда, Функция, непрерывная на отрезке, принимает любое значение, заключенное между ее наименьшим и наибольшим значениями. Поэтому, в частности, найдется такое число с Î [a, b], что что и требовалось доказать. 

44)Формула Ньютона-ЛейбницаПусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то

45)Геометрические и физические приложения определенного интеграла: 1. Площадь криволинейной трапеции, ограниченной кривой y =f(x)( f(x)>0), прямыми x = a , x = b и отрезком [ a , b ] оси Ох, вычисляется по формуле 2. Площадь фигуры, ограниченной кривыми y = f ( x ) и y = g ( x ) ( f ( x )< g ( x )) и прямыми х= a , x = b , находится по формуле 3. Если кривая задана параметрическими уравнениями x = x ( t ), y = y ( t ), то площадь криволинейной трапеции, ограниченной этой кривой и прямыми х=a , x= b , находится по формуле 4. Пусть S ( x )- площадь сечения тела плоскостью, перпендикулярной оси Ох, тогда объем части тела, заключенной между перпендикулярными оси плоскостями х=а и х= b , находится по формуле 5. Пусть криволинейная трапеция, ограниченная кривой y = f ( x ) и прямыми y=0, х=а и х= b , вращается вокруг оси Ох, тогда объем тела вращения вычисляется по формуле 6. Пусть криволинейная трапеция, ограниченная кривой х= g ( y ) и прямыми x =0, y = c и y = d , вращается вокруг оси О y , тогда объем тела вращения вычисляется по формуле 7. Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением y = f ( x ) (или x = F ( y )), то длина дуги определяется формулой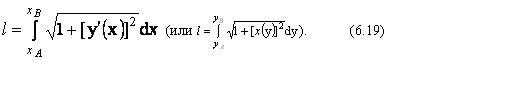