7)Предел и непрерывность суммы,произведения и частного:

8)Предел обратной ф-ии:теорема:пусть дана ф-ия y=f(x),f(x)-строго монотонная(либо возрастающая.либо убывающая);x2>x1=>f(x2)>f(x1);убывающая x2>x1=>f(x2)<любого(x1)и lim(x->a)f(x)=b,Тогда нужно показать,что для любой окрестности т.А существует окрестность в т.В;Возьмём произвольную окрестность Uа и выберем 2 точки х1 и х2:х1<a,x2>a т.к.дана прямая ф-ия y=f(x),то Е f(x1)и f(x2)и т.к. f(x)-монотонная(пусть возрастающая),то f(x1)<f(x2)

9)понятие одностороннего предела: Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны.Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва). Пусть на некотором числовом множестве   задана числовая функция   и число   — предельна точка области определения  . Существуют различные определения для односторонних пределов функции   в точке  , но все они эквивалентны.

10)О соотношении обычного предела с односторонними:

11)Непрерывность элементарных ф-ий:Одним из важнейшиных свойств элементарных ф-ий является их непрерывность в каждой точке, в окрестности которой они определены.На примере некоторых функций проверим данный факт,используя определение непрерывности функции в точке.1)непрерывность рациональных ф-ий:Простейшим примером ф-ии,непрерывной в любой т.Х0 числовой прямой,может служить постоянная функции f(x)=C.Действительно в этом случае lim(x->x0)f(x)=C=f(x0),т.е.постоянная ф-ия непрерывна в каждой точке числовой прямой.непрерывна также в каждой точке x0числовой прямой ф-ия f(x)=x,т.к. lim(x->x0)x=x0==f(x0).т.е.постоянная ф-ия в точке х0 равен ее значению в этой точке.

12)Бесконечно-малые и бесконечно большие функции:Функция y=f(x)называется бесконечно малой при x→a или при x→∞,если   или  ,т.е.бесконечно малая функция–это функция,предел которой в данной точке равен нулю.П римеры.1)Функция f(x)=(x-1)² является бесконечно малой при x→1, так как   (см. рис.).2)Функция f(x) = tgx – бесконечно малая при x→0. 3)f(x) = ln (1+x)– бесконечно малая при x→0. 4)f(x) = 1/x– бесконечно малая при x→∞.Установим следующее важное соотношение:Теорема.Если функция y=f(x)представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x):f(x)=b+α(x)то  .Обратно,если  ,то f (x)=b+α(x),где a(x) – бесконечно малая при x→a.Доказательство:1)Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a,при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что  .2)Если  , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.

13)

14)Принцип двойных неравенств:Когда два неравенства соединены словом и,или,тогда формируется двойное неравенство. Двойное неравенство, как -3<2x+5 и 2x+5≤7 называется соединённым,потому что в нём использовано и.Запись -3<2x+5≤7является сокращением для предыдущего неравенства.Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.Пример 2 Решите -3 < 2x + 5 ≤ 7. Постройте график множества решений.Решение У нас есть Множество решений есть {x| - 4 < x ≤ 1}, or (-4, 1]. График множества решений изображён ниже. Двойное неравенство, как 2x - 5 ≤ -7 или называется разделённым, потому что оно содержит или. В отличие от некоторых соединённых неравенств, оно не может быть сокращено; поэтому, оно не может быть записано безили.

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)Возрастание и убывание функции:Возрастание и убывание функции:функция y=f(x) называется возрастающей на отрезке[a, b],если для любой пары точек х и х',а≤х<х'≤ b выполняется неравенство f(x)≤f(x'),и строго возрастающей-если выполняется неравенство f(x)<f(x').Аналогично определяется убывание и строгое убывание функции.Например, функция у=х²(рис.,а)строго возрастает на отрезке[0,1],а (рис.,б)строго убывает на этом отрезке.Возрастающие функции обозначаются f (x)↑,а убывающие f(x)↓.Для того чтобы дифференцируемая функция f(x)была возрастающей на отрезке [а, b],необходимо и достаточно,чтобы её производная f'(x)была неотрицательной на[а,b].Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке.Функция у=f(x) называется возрастающей в точке x₀,если найдётся такой интервал(α,β),содержащий точку x₀,что для любой точки х из(α,β),х>x₀, выполняется неравенство f(x₀)≤f(x),и для любой точки х из(α,β),х< x₀,выполняется неравенство f(x)≤ f(x₀).Аналогично определяется строгое возрастание функции в точке x₀.Если f'(x₀)>0,то функция f(x) строго возрастает в точке x₀.Если f(x) возрастает в каждой точке интервала (a,b),то она возрастает на этом интервале.

 

28)ЭКСТРЕМУМ ЛОКАЛЬНЫЙ:ЭКСТРЕМУМ ЛОКАЛЬНЫЙ:Значение функционала в точке,в к-рой выполняется следующее условие:существует такая окрестность точки,что наименьшего(наибольшего)значения в данной окрестности функционал достигает именно в рассматриваемой точке.

29)ТЕОРЕМЫ Вейерштрасса,ФЕРМА,РОЛЛЯ,ЛАГРАНЖА:Теорема Ферма:Если функция у=f(х),определенная в интервале (а;b),достигает в  некоторой точке с этого интервала наибольшего(или наименьшего)значения и существует  производная f ′(с),то f ′(с)=0.Геометрический смысл этой теоремы состоит в том,что касательная к графику функции у=f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).  Теорема Ролля:Если функция у=f(х),непрерывная на отрезке[а;b]и  дифференцируемая в интервале(а;b), принимает на концах этого отрезка равные значения f(a)=f(b),то в интервале(а;b)существует такая точка С,что f′(с)= 0. Геометрически эта теорема означает  следующее:если крайние ординаты кривой у=f(х)равны,то на кривой найдется точка, в которой касательная параллельна оси абсцисс(рис.).   Теорема Лагранжа:Если функция у=f(х)непрерывна на отрезке[а;b] и  дифференцируема в интервале(а;b),то в этом интервале найдется такая точка с,что Эта теорема имеет простой геометрический смысл(рис.):на графике функции у = f (х)  между точками А и В найдется такая внутренняя точка С,что касательная к графику в точке С параллельна хорде АВ.   Следствие.Если f′(x)=0 в интервале(а;b),то в этом интервале функция f(х)постоянна.  

30)Правило Лопиталя:Правило Лопиталя:представляет собой метод вычисления пределов,имеющих неопределенность типа или .Пусть a является некоторым конечным действительным числом или равно бесконечности.Если и ,то ;Если и ,то аналогично .Это правило впервые упоминалось в книге по дифференциальному исчислению,опубликованной в 1696 году французским математиком Гийомом Лопиталем(1661-1704). Правило Лопиталя можно также применять к неопределенностям типа  . Первые две неопределенности   можно свести к типу   или   с помощью алгебраических преобразований.А неопределенности   сводятся к типу  с помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов. ПРИМЕР:Вычислить предел  .Решение.Дифференцируя числитель и знаменатель, находим значение предела:

31)Дифференциальные признаки монотонности и постоянства функции: Теорема.Пусть  непрерывна на промежутке , тогда:1)если,то функция  возрастает(убывает)на.2)если,то функция  строго возрастает(строго убывает)на .Доказательство:для случая возрастания:Пусть.Возьмем для  возрастает.Геометрический смысл теоремы2:Если,то касательная везде образует положительный острый угол, т.е. функция идет вверх.

32)Расположение графика ф-ии относительно касательной:1)Касательная есть предельное положение секущей при  2)Касательная к графику дифференцируемой в точке х₀функции f-это прямая,проходящая через точку(х₀;f(x₀))и имеющая угловой коэффициент f ^\(х₀).3)Касательной к графику функции называется прямая,имеющая с данной кривой единственную общую точку.пример:Прямая х=2 имеет с параболой у=(х-1)²одну общую точку(2;1),но касательной не является.Прямая у=2х-3,проходящая через эту точку,является касательной к графику данной функции.Покажем это.Мы знаем, что если существует производная функции у=f(x)в точке х₀,то существует и касательная к графику этой функции. Уравнение касательной имеет вид:у= f(x₀)+f ^\(x₀)(х-х₀);у ^\(х)=2х-2, у ^\(х₀)=у ^\(2)=2, у(х₀)=у(2)=1.Уравнение касательнойу=1+2(х-2)=2х-3, у=2х-3.

33)Точки Выпуклости и перегиба функции:Непрерывная на отрезке[a;b]функция f (x)называется выпуклой вверх на этом отрезке,если для любых точек x₁ и x₂ из этого отрезка 

Выпуклая вверх функция.

Другими словами, если для любых точек x₁ и x₂ отрезка[a;b]секущая AB проходит под графиком функции f(x),то функция f выпукла вверх.Аналогично определяется функция,выпуклая вниз.Дважды дифференцируемая на[а;b]функция f(x)выпукла вверх,если для любого 

Дважды дифференцируемая на[a;b]функция f(x)выпукла вниз,если для любого 

Так,вторая производная функции   равна   откуда следует,что квадратичная функция выпукла вниз на всей области определения.Пусть функция f(x)непрерывна в точке   и имеет в этой точке конечную или бесконечную производную.Тогда точка  называется точкой перегиба функции f,если в этой точке изменяется направление ее выпуклости.Необходимое условие наличия точки перегиба:Если  –точка перегиба функции f(x),и функция f(x) имеет вторую производную,непрерывную в этой точке,то 

Достаточные условия наличия точки перегиба.Пусть функция f(x)непрерывна и имеет конечную или бесконечную производную в точке   Если   меняет знак при переходе через точку   то   –точка перегиба функции f(x).Если     то   –точка перегиба функции f(x).В заключение приведем примеры,когда точка x₀ не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:если функция разрывна в точке   (например      );в случае угловой точки (например,     Не являются точками перегиба и точки возврата,например точка   у функции 

 Все вышеперечисленные случаи изображены на рисунке.

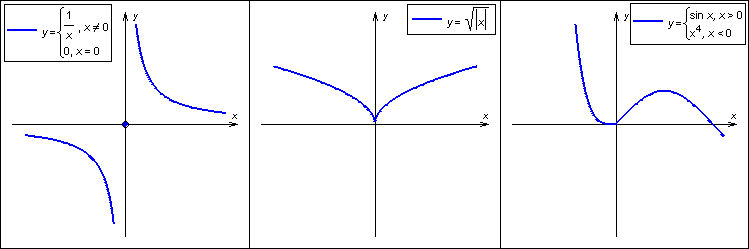
34)Схема исследования ф-ии: 1.Область определения2.Исследование функции на четность,нечетность и периодичность.Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  ,то  –четная функция;если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство  , то  – нечетная функция; в противном случае, –общего вида.График четной функции симметричен относительно оси ординат,график нечетной функции симметричен относительно начала координат.3.Нахождение точек пересечения графика функции с осями координат.Точки пересечения с осью ОХ: ,где  –решение уравнения  .Точки пересечения с осью ОY:  .4.Нахождение промежутков знакопостоянства функции.Промежутки знакопостоянства функции – промежутки из области определения функции,где функция принимает положительные или отрицательные значения, т.е.   или  5.Нахождение производной функции, области определения производной, критических точек.Критические точки функции–внутренние точки области определения функции, в которых производная не существует или равна нулю.6.Нахождение промежутков возрастания,убывания,точек экстремума и экстремумов.Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.7.Нахождение промежутков выпуклости функции и точек перегиба.Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.8.Исследование поведения функции на бесконечности и в окрестности точек разрыва.Для исследования поведения функции в окрестности точки разрыва   необходимо вычислить односторонние пределы:   и   . Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая   – вертикальная асимптота.При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при   и  . Для этого нужно вычислить следующие пределы:  и   . Если оба предела существуют, то   – уравнение наклонной асимптоты при  . Частный случай наклонной асимптоты при   – горизонтальная асимптота.  Аналогично ищется наклонная асимптота при  . 9.Построение графика (при необходимости нужно найти значения функции в дополнительных точках)

35)Понятие первообразной:Функция F(х)называется первообразной функцией для  данной функции f(х)(или, короче,первообразной данной функции f(х))на данном промежутке,если на этом промежутке    Пример.Функция   является  первообразной функции на всей числовой оси,так как при любом х.Отметим,что вместе с  функцией первообразной для является любая функция вида ,где С-произвольное постоянное число(это следует из того,что производная постоянной равна нулю).Это свойство имеет место и в общем случае.Теорема 1.Если и -две  первообразные для функции f(х) в некотором промежутке,то разность между ними в этом промежутке равна постоянному числу.Из этой теоремы следует,что если известна какая-нибудь первообразная F(х) данной  функции f(х),то все множество первообразных для f(х) исчерпывается функциями F(х)+С.Выражение F(х)+С,где F(х)-первообразная функции f(х)иС-произвольная постоянная,называется неопределенным интегралом от функции f(х) и обозначается символом  ,  причем f (х) называется подынтегральной функцией; -подынтегральным выражением,х-переменной  интегрирования;∫-знак неопределенного интеграла.Таким образом,по определению    если 

36)Основные свойства неопределенного интеграла:1.Производная от н.и.равна подынтегральной функции,а дифференциал-подынтегральному выражению: 2. в частности, Свойства 1,2следуют из определения н.и. 3.Н.и.от алгебраической суммы конечного числа функций равен алгебраической сумме н.и.от каждого слагаемого.Докажем,что (Равенство понимается с точностью до постоянного слагаемого.)Действительно,по 1: Таким образом,левая и правая части имеют одинаковые производные и могут отличаться лишь постоянной. 4.Постоянный множитель можно выносить за знак н.и: 5. Независимость вида н.и. от выбора аргумента(инвариантность формы интеграла): где    имеет непрерывную производную.Действительно, по свойству инвариантности формы дифференциала: Частным случаем 5° является = F(ax + b) + с.Очевидно, учитывая, что d(ax + b) = a dx, получаем формулу