
- •Введение
- •1 Анализ состояния вопроса
- •1.1 Свойства звукоизоляции и звукопроницаемости материалов
- •1.2 Конструкции объектов и звук
- •1.2.1 Распространение звука в ограниченном пространстве
- •1.2.2 Звукопоглощающие материалы и конструкции
- •1.3 Параметры звуковых сигналов. Методы измерения
- •1.3.1 Звуковое поле в неограниченном пространстве
- •1.3.2 Линейные характеристики
- •1.3.3 Энергетические характеристики
- •1.3.4 Плоская волна
- •1.3.5 Сферическая волна
- •1.3.6 Цилиндрическая волна
- •1.3.7 Основные свойства слуха
- •1.4 Акустические сигналы
- •1.4.1 Определения
- •1.4.2 Динамический диапазон
- •1.4.3 Средний уровень
- •1.4.4. Частотный диапазон и спектры
- •1.4.5 Временные характеристики сигнала
- •1.4.6 Первичный речевой сигнал
- •1.4.7 Вторичный сигнал
- •1.4.8 Шумы и помехи
- •1.4.9 Линейные искажения
- •1.4.10 Нелинейные искажения
- •1.4.11 Переходные искажения
- •1.4.12 Допустимые величины искажений
- •1.5 Излучение и приём акустических сигналов.
- •1.5.1 Микрофоны
- •1.5.2 Громкоговорители и телефоны
- •2 Методика выполнения измерений
- •2.1 Определение звукоизоляции образца звукоизоляционного материала с помощью акустического интерферометра
- •2.2 Метод измерений
- •2.7 Подготовка к проведению измерений. Выполнение измерений
- •2.7.1 Подготовка к проведению измерений
- •2.7.2 Выполнение измерений
- •2.8 Нормативные ссылки
- •3 Оценка погрешности измерений звукоизоляции образца
- •3.1 Методическая погрешность
- •3.2 Инструментальная погрешность
- •3.2.1 Микрофонная база
- •3.2.2 Анализатор
- •3.2.3 Громкоговоритель иаи
- •4 Экспериментальные данные
- •5 Безопасность жизнедеятельности
- •5.1 Охрана труда
- •5.1.1 Порядок обеспечения работников специальной одеждой
- •5.2 Защита в чрезвычайных ситуациях
- •5.2.1 Назначение, принцип действия и виды автоматического пожаротушения на производстве
- •6 Экономический расчет
- •6.1 Расчет трудоемкости дипломной работы
- •Заключение
- •Библиографический список
1.3 Параметры звуковых сигналов. Методы измерения
1.3.1 Звуковое поле в неограниченном пространстве
Звуковым
полем
называют
пространство, в котором происходит
распространение звуковых колебаний.
Звуковые колебания в жидкой и
газообразной средах представляют собой
продольные колебания, так как частицы
среды колеблются вдоль линии
распространения звука. Вследствие
этого образуются сгущения 1
и разрежения 2
среды,
двигающиеся от источника колебаний
(рис. 1.1) с определенной скоростью,
называемой скоростью
звука.
Скорость
звука в воздухе при температуре
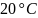 и нормальном атмосферном давлении
приблизительно равна 340
и нормальном атмосферном давлении
приблизительно равна 340
 .
.
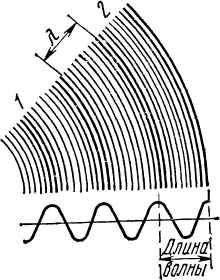
Рисунок 1.1 – Распространение звуковых волн
Волнообразное изменение плотности среды, вызванное звуковыми колебаниями, называют звуковой волной. Направление распространения звуковых волн – звуковым лучом, а поверхность, соединяющую смежные точки поля с одинаковой фазой колебания (например, точки максимального сгущения или разрежения), – фронтом волны. Звуковые лучи пересекают фронт волны под прямым углом. В общем случае фронт волны имеет сложную форму, но в большинстве практических случаев можно ограничиться соотношениями, полученными для плоской и сферической форм фронта, а иногда еще и цилиндрической.
Если
период
колебаний
 ,
то
частота
колебаний
,
то
частота
колебаний
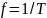 ,
а длина
звуковой волны, равная
расстоянию между соседними фронтами,
находящимися в одинаковой фазе (рис.
1.1), –
,
а длина
звуковой волны, равная
расстоянию между соседними фронтами,
находящимися в одинаковой фазе (рис.
1.1), –
 ,
где
,
где
 – скорость
звука.
– скорость
звука.
В системах связи и вещания частоты колебаний лежат в пределах от 20–30 до 15000–20000 Гц, соответственно длины звуковых волн от 17–11,3 м до 2,27–1,7 см.
Частоты колебаний подразделяют на низкие, средние и высокие звуковые частоты. К низким относят частоты, лежащие в пределах от 20 до 200–500 Гц, к высоким звуковым частотам от 2000–5000 до 20000 Гц, к средним – промежуточные между высокими и низкими. Частоты, лежащие ниже 20 Гц, называют инфразвуковыми, а выше 20 кГц – ультразвуковыми [3].
Звуковое поле характеризуют рядом линейных и энергетических величин.
1.3.2 Линейные характеристики
Звуковое
давление. Положим, что давление среды
в отсутствие звуковых колебаний равно
 ,
это давление называют статическим.
При
прохождении звуковой волны давление
в каждой точке среды будет непрерывно
изменяться: в моменты сгущения частиц
оно больше статического, а в моменты
разрежения – меньше. Разность между
мгновенным давлением
,
это давление называют статическим.
При
прохождении звуковой волны давление
в каждой точке среды будет непрерывно
изменяться: в моменты сгущения частиц
оно больше статического, а в моменты
разрежения – меньше. Разность между
мгновенным давлением
 и статическим
в той же точке среды, т. е. переменная
составляющая давления (часто звуковое
давление называют избыточным давлением
среды, такое название ассоциируется с
положительным приращением давления),
называется звуковым
давлением
и статическим
в той же точке среды, т. е. переменная
составляющая давления (часто звуковое
давление называют избыточным давлением
среды, такое название ассоциируется с
положительным приращением давления),
называется звуковым
давлением
 .
.
Звуковое
давление – величина знакопеременная.
Давление
 –
сила, действующая на единицу площади,
т. е.
–
сила, действующая на единицу площади,
т. е.
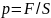 .
Поэтому
за единицу давления в системе СИ
принимают ньютон на квадратный метр
.
Поэтому
за единицу давления в системе СИ
принимают ньютон на квадратный метр

 (паскаль)
(паскаль)

 .
В системах связи и вещания имеют дело
с звуковыми давлениями, по амплитуде,
не превышающими 100 Па, т. е., по крайней
мере, в 1000 раз меньше, чем нормальное
атмосферное давление.
.
В системах связи и вещания имеют дело
с звуковыми давлениями, по амплитуде,
не превышающими 100 Па, т. е., по крайней
мере, в 1000 раз меньше, чем нормальное
атмосферное давление.
Скорость
колебаний. Если давления неодинаковы
в соседних точках среды, то ее частицы
стремятся сместиться в сторону
минимального давления. При знакопеременной
разности давлений возникает колебательное
движение частиц среды около своего
статического положения. Скорость
колебаний этих
частиц
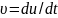 ,
где
,
где
 – смещение
частиц. Скорость колебаний обычно
измеряют в метрах или сантиметрах в
секунду. Не следует путать эту скорость
со скоростью звука. Скорость звука –
постоянная величина для данной среды
и метеорологических условий, а скорость
колебаний – переменная, причем если
частица среды
перемещается по
направлению распространения волны, то
скорость считают положительной, а при
обратном перемещении частицы –
отрицательной.
– смещение
частиц. Скорость колебаний обычно
измеряют в метрах или сантиметрах в
секунду. Не следует путать эту скорость
со скоростью звука. Скорость звука –
постоянная величина для данной среды
и метеорологических условий, а скорость
колебаний – переменная, причем если
частица среды
перемещается по
направлению распространения волны, то
скорость считают положительной, а при
обратном перемещении частицы –
отрицательной.
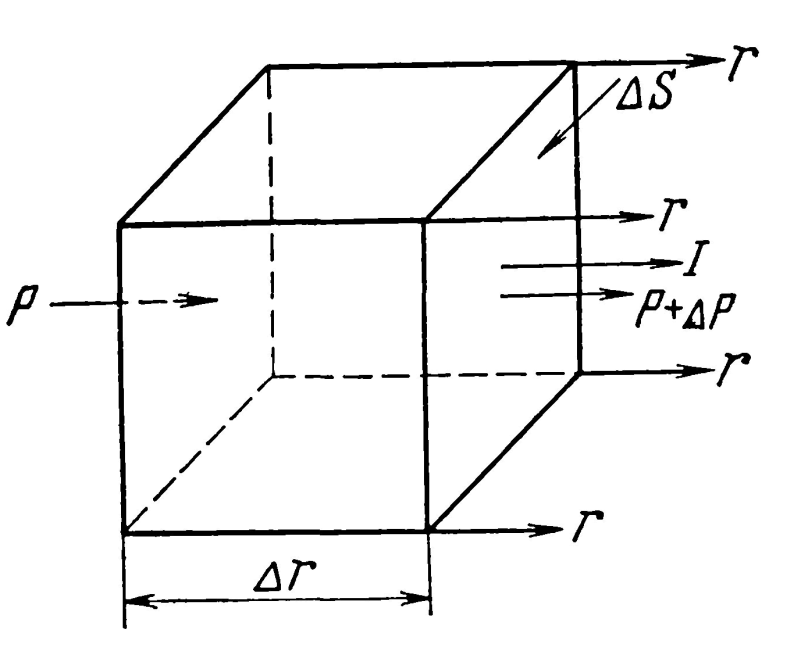
Рисунок 1.2 – Вывод уравнения движения
Определим
связь между звуковым давлением и
скоростью колебаний. Возьмем
элементарный объем, заключенный
между фронтами волн, находящимися на
расстоянии
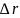 друг от друга, с боковыми поверхностями,
расположенными вдоль звуковых лучей
(рис. 1.2). Как видно из рисунка, среда в
этом объеме находится под действием
разности давлений
и
друг от друга, с боковыми поверхностями,
расположенными вдоль звуковых лучей
(рис. 1.2). Как видно из рисунка, среда в
этом объеме находится под действием
разности давлений
и
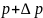 ,
следовательно,
испытываемая ею сила
,
следовательно,
испытываемая ею сила
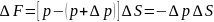 ,
где
,
где
 – площадь, выделенная на поверхности
фронта волны. С другой стороны, по второму
закону Ньютона сила инерции
– площадь, выделенная на поверхности
фронта волны. С другой стороны, по второму
закону Ньютона сила инерции
 ,
где
,
где
 – масса среды, заключенной в этом объеме;
– масса среды, заключенной в этом объеме;
 – средняя плотность среды. Так как в
вещании и связи имеют дело с изменением
плотности среды не более чем на 0,1%,
в дальнейшем индекс у
– средняя плотность среды. Так как в
вещании и связи имеют дело с изменением
плотности среды не более чем на 0,1%,
в дальнейшем индекс у
 опускаем. Приравнивая обе силы,
получаем
опускаем. Приравнивая обе силы,
получаем
 .
Так как
и
.
Так как
и
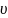 зависят
как от координат, так и от времени, то,
переходя к производным, имеем
зависят
как от координат, так и от времени, то,
переходя к производным, имеем
 .
(1.5)
.
(1.5)
Это уравнение называется уравнением движения среды.
Деформация идеальной (невязкой) газообразной среды, появляющаяся при распространении в ней звуковой волны, является адиабатической, так как звуковые процессы происходят быстро, без теплообмена. Поэтому эти процессы подчиняются закону Бойля-Мариотта с поправкой Пуассона.

Рисунок 1.3 – Вывод уравнения непрерывности
 ,
где
,
где
 – показатель адиабаты для воздуха
– показатель адиабаты для воздуха
 .
Выделяем элементарный объём
.
Выделяем элементарный объём
 (рис. 1.3) как и в предыдущем случаи. В
статистическом состоянии в нем находится
определенное количество частиц среды.
При звуковых колебаниях занимаемый ими
объём непрерывно изменяется. Положим,
что в некоторый момент частицы среды
слева будут смещены на величину
,
а справа – на величину
(рис. 1.3) как и в предыдущем случаи. В
статистическом состоянии в нем находится
определенное количество частиц среды.
При звуковых колебаниях занимаемый ими
объём непрерывно изменяется. Положим,
что в некоторый момент частицы среды
слева будут смещены на величину
,
а справа – на величину
 ,
тогда, при условии непрерывности среды
этот объем
,
тогда, при условии непрерывности среды
этот объем
 Разделим обе части выражения на
Разделим обе части выражения на
 и
в правой части заменим
на
и
в правой части заменим
на
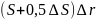 .
.
При
пренебрежении членами второго порядка
малости получим
 .
Заметим, что последний член в этом
выражении обусловлен расхождением
(дивергенцией)
франта
волны.
.
Заметим, что последний член в этом
выражении обусловлен расхождением
(дивергенцией)
франта
волны.
При
звуковых колебаниях полное давление
газообразной среды
 ,
где
– статическое давление;
– звуковое давление. Следовательно,
,
где
– статическое давление;
– звуковое давление. Следовательно,
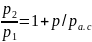 .
Подставив
.
Подставив
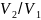 и
и
 в уравнение закона
Пуассона, получим
в уравнение закона
Пуассона, получим
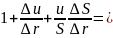 .
Как указывалось ранее
.
Как указывалось ранее
 ,
поэтому
,
поэтому
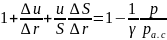 или
или

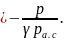 Переходя
к производным, находим
Переходя
к производным, находим
 .
(1.6)
.
(1.6)
Это
уравнение называют уравнением
состояния среды. Если
это уравнение продифференцировать
дважды по
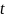 и переставить порядок дифференцирования,
то получим
и переставить порядок дифференцирования,
то получим
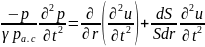 .
Подставляя в него производную
.
Подставляя в него производную
 из уравнения движения (1.5), получим
уравнение для звукового давления
из уравнения движения (1.5), получим
уравнение для звукового давления
 .
Заменяя в нем
.
Заменяя в нем
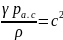 ,
(1.7)
,
(1.7)
получим
 .
(1.8)
.
(1.8)
Это уравнение называют волновым уравнением Вебстера.
Общее волновое уравнение имеет вид
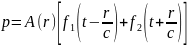 .
(1.9)
.
(1.9)
Если
в первую составляющую решения вместо
подставить
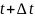 ,
то
для неизменности аргумента следует
вместо
подставить
,
то
для неизменности аргумента следует
вместо
подставить
 .
Следовательно,
первая составляющая представляет собой
волну, распространяющуюся в сторону
положительных значений
,
вторая – в обратном направлении. Из тех
же данных следует, что
–
скорость распространения волны, так
как
.
Следовательно,
первая составляющая представляет собой
волну, распространяющуюся в сторону
положительных значений
,
вторая – в обратном направлении. Из тех
же данных следует, что
–
скорость распространения волны, так
как
 .
Таким
образом, скорость звука
.
Таким
образом, скорость звука
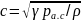 ,
т. е. определяется статическим давлением
среды и ее плотностью [2].
,
т. е. определяется статическим давлением
среды и ее плотностью [2].
Акустическое сопротивление. Разность давлений является причиной движения частиц среды, а разность потенциалов – причиной движения электрических зарядов. Скорость колебаний частиц среды аналогична скорости движения зарядов – силе тока. Аналогично электрическому сопротивлению введено понятие волнового акустического сопротивления. Удельным волновым акустическим сопротивлением называют отношение звукового давления к скорости колебаний. Удельным оно называется потому, что представляет собой сопротивление для единицы площади фронта волны. Для краткости его часто называют акустическим сопротивлением
 .
(1.10)
.
(1.10)
Акустическое сопротивление определяется прежде всего свойствами среды. В ряде случаев оно зависит от частоты колебаний и от формы фронта волны. В общем виде оно комплексное:
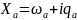 ,
(1.11)
,
(1.11)
где
 и
и
 – активная
и реактивная составляющие
акустического сопротивления. Наличие
реактивной составляющей свидетельствует
о том, что между звуковым давлением
и скоростью колебаний есть сдвиг
фаз. Этот
сдвиг определяется из соотношения
– активная
и реактивная составляющие
акустического сопротивления. Наличие
реактивной составляющей свидетельствует
о том, что между звуковым давлением
и скоростью колебаний есть сдвиг
фаз. Этот
сдвиг определяется из соотношения
 .
(1.12)
.
(1.12)
