5. Вычисление площадей плоских фигур.

.

Если требуется найти площадь фигуры, ограниченной графиками двух функций: f₁(x) и f₂(x) (рис. 2), то ее можно рассматривать как разность площадей двух криволинейных трапеций: верхней границей первой из них служит график функции f₂(x), а второй – f₁(x).

Если требуется определить объем так называемого тела вращения, то есть тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной частью графика функции y = f(x) от х = а до x = b и отрезками прямых х = а, х = b и у =0, то площадь сечения такого тела плоскостью x = const равна , и формула (14.8) в этом случае имеет вид:

Вычисление длины дуги.

Теорема. Пусть функции x(t) и y(t) имеют на отрезке непрерывные производные и . Тогда длина дуги кривой

.

6. Если существует конечный предел ,

то его называют несобственным интегралом 1-го рода от функции f(x) на интервале и обозначают 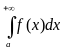. Таким образом, по определению

= . (15.2)

При этом говорят, что несобственный интеграл существует или сходится. Если же не существует конечного предела (15.1), несобственный интеграл не существует или расходится.

Пусть функция f(x) определена и непрерывна при a ≤ x < b и имеет разрыв при x = b. Тогда определяется следующим образом:

и называется несобственным интегралом 2-го рода. Если предел, стоящий справа, существует и конечен, интеграл называется сходящимся, в противном случае – расходящимся.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей.

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Действия над комплексными числами

• Сложение (a + bi) + (c + di) = (a + c) + (b + d)i

• Вычитание (a + bi) − (c + di) = (a − c) + (b − d)i

• Умножение (a + bi)(c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i

• Деление Тригонометрическая и показательная формыЕсли вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент ( 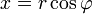, ), то комплексное число z можно записать в тригонометрической форме .

1 Уравнения, в которые неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями. Подобными уравнениями описываются многие физические явления и процессы.

Уравнение вида

называется обыкновенным дифференциальным уравнением п-го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.

Дифференциальное уравнение первого порядка в общем случае можно записать в виде

F(x;y;y')=0.

Уравнение связывает независимую переменную х, искомую функцию y и ее производную y'. Если уравнение (2.1) можно разрешить относительно y', то его записывают в виде

У'=ƒ(х;у) и называют ДУ первого порядка, разрешенным относительно производной.

Уравнения с разделяющимися переменными.

Дифференциальные уравнения вида

f₂(y)dy = f₁(x)dx называются уравнениями с разделяющимися переменными. Тогда любое решение у(х) этого уравнения будет удовлетворять и уравнению

,где с – произвольная постоянная. Если удается найти первообразные функций f₁(x) и f₂(y), выраженные в элементарных функциях, то из (17.2) можно получить конечное уравнение вида Ф (х , у) = 0,

которое определяет решение у(х) уравнения (17.1) как неявную функцию х.

1. К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка, имеющие вид:

Действительно, замена или y = xt приводит к

Еще одной формой однородного уравнения является уравнение

M(x,y) dx + N(x,y) dy = 0, если М(х,у) и N(x,y) – однородные функции одинаковой степени однородности. При этом .

2. Линейным дифференциальным уравнением первого порядка называется уравнение вида

, (17.8)

линейное относительно неизвестной функции у(х) и ее производной. При этом будем предполагать, что р(х) и f(x) непрерывны.

В случае, когда f(x) ≡ 0, уравнение (17.8) называется однородным. Такое уравнение является уравнением с разделяющимися переменными:

, откуда

К линейным уравнениям можно свести с помощью замены некоторые другие дифференциальные уравнения, например, уравнение Бернулли:

Разделив на у^п, получим: , а замена z = y^1-n , приводит к линейному уравнению относительно z:

.

3. Рассмотрим дифференциальное уравнение п-го порядка:

F (x, y, y′,…, y⁽ⁿ⁾) = 0,

где F предполагается непрерывной функцией всех своих аргументов. Тогда по теореме о существовании неявной функции (см. лекцию ) можно разрешить это уравнение относительно старшей производной:

у^(п) = f (x, y, y′,…, y^(n-1))

и сформулируем для него (без доказательства) теорему существования и единственности решения:

Теорема 18.1. Существует единственное решение уравнения (18.2), удовлетворяющее условиям , если в окрестности начальных значений (х₀ , у₀ , у′₀ ,…, у₀^(п-1)) функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго.

Уравнения, допускающие понижение порядка.

1. Уравнение не содержит искомой функции и ее производных по порядок (k – 1) включительно:

. В этом случае можно сделать замену р = у^(k), которая позволяет понизить порядок уравнения до n – k, так как после замены уравнение примет вид

.

Из этого уравнения можно найти р = р (х, С₁ , С₂ ,…, С_n-k), а затем найти у с помощью интегрирования k раз функции р = р (х, С₁ , С₂ ,…, С_n-k).

2. Уравнение не содержит независимой переменной:

F ( y, y′,…, y⁽ⁿ⁾) = 0

Порядок такого уравнения можно понизить на единицу заменой у′ = р(у). При этом производные функции f(x) по аргументу х нужно выразить через производные р по у:

и т.д.

3. Уравнение F (х, y, y′,…, y⁽ⁿ⁾) = 0 однородно относительно аргументов y, y′,…, y⁽ⁿ⁾, то есть справедливо тождество

В этом случае можно понизить порядок уравнения на единицу, вводя новую неизвестную функцию z, для которой . Тогда и т.д.

1. Числовой ряд – это сумма членов числовой последовательности вида

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

Свойства сходящихся числовых рядов.

Если сходится числовой ряд , то сходящимся будет и ряд . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд , причем , где A – произвольная постоянная.

Если сходятся числовые ряды и , их суммы равны A и B соответственно, то сходящимися будут ряды и , причем их суммы будут равны A + B и A - B соответственно.

Необходимое условие сходимости ряда. Если числовой ряд сходится, то предел его k-ого члена равен нулю : .

При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если , то ряд расходится.

С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства не говорит о сходимости числового ряда .

2. Сумма вида называется гармоническим числовым рядом.

ГАРМОНИЧЕСКИЙ РЯД ЯВЛЯЕТСЯ РАСХОДЯЩИМСЯ.

Докажем расходимость гармонического ряда.

Предположим, что ряд сходится. Тогда существует конечный предел его частичных сумм. В этом случае можно записать и , что приводит нас к равенству .

С другой стороны,

Не вызывают сомнения следующие неравенства . Таким образом, . Полученное неравенство указывает нам на то, что равенство не может быть достигнуто, что противоречит нашему предположению о сходимости гармонического ряда.

Вывод: гармонический ряд расходится.