25.Линейные дифференциальные уравнения первого порядка

Определение. Линейными дифференциальными уравнениями первого порядка называются уравнения, линейные относительно неизвестной функции и её производной.

Линейное дифференциальное уравнение имеет вид:

(20)

где и  непрерывные функции от .

Замечание 1. и входят в уравнение (20) только в первой степени.

Замечание 2. или могут быть постоянными числами, если же они одновременно являются константами, то уравнение (20) будет уравнением с разделяющимися переменными.

Пример 10. Рассмотрим дифференциальное уравнение

Решение. Полагая, что х  0, разделим обе части равнения на , получим

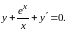
Перенесем слагаемое в правую сторону, тогда

Данное уравнение является линейным, так как содержит у и у' только в первой степени,

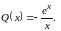
26.Уравнение Бернулли Определение. Уравнение вида

называется уравнением Бернулли, где и  непрерывные функции от , , .

Замечание. При получается линейное уравнение первого порядка относительно и , а при получается уравнение с разделяющимися переменными.

Уравнение Бернулли приводится к линейному следующим образом:

Разделим все члены уравнения (24) на

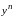
Сделаем замену:

Тогда

Подставим в уравнение вместо

Умножим полученное уравнение на :

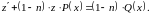
Преобразованное уравнение является линейным относительно и . Решив его, найдем общий интеграл уравнения Далее, подставив , получим общее решение уравнения Бернулли

Замечание. При интегрировании уравнений Бернулли можно сразу применить подстановку , не преобразовывая их в линейные.

27.Уравнение в полных дифференциалах

Определение. Дифференциальное уравнение первого порядка вида

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , то есть

Для того чтобы уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие

Уравнение может быть записано в виде

Тогда общий интеграл этого уравнения имеет вид

где  произвольная постоянная.

Функция может быть найдена, используя уравнения

Интегрируя равенство по при фиксированном и учитывая, что произвольная постоянная в этом случае может зависеть от , получим 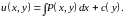Затем, дифференцируя найденную функцию по и подставляя её в равенство , найдем .Подставим функцию в уравнение (31), получим , которая является общим интегралом уравнения (27) с точностью до произвольной постоянной.

28.Ду высших порядков…..

Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида F(x, y, y', y'', ..., y⁽ⁿ⁾) = 0,  где F - известная функция (n+2) переменных, определенная в области D М Rⁿ+2, x - независимая переменная из интервала (a, b), y = y(x) - неизвестная функция, n - порядок уравнения.

 

ПРИМЕР Уравнение движения материальной точки.

 Функция y(x) называется решением дифференциального уравнения n-го порядка, если онаn раз непрерывно дифференцируема на промежутке (a, b) и удовлетворяет  уравнению для всех  xО(a, b).

 

Дифференциальное уравнение n-го порядка имеет, вообще говоря, бесконечное множество решений. Чтобы выделить единственное решение уравнения достаточно определить начальные условия: y(x₀) = y₀ , y'(x₀) = y_0,1 , y''(x₀) = y_0,2 , ..., y^(n-1)(x₀) = y_0,n-1.

При определенных ограничениях на правую часть уравнения эта задача, она называется задачей Коши, имеет единственное решение.

Задача о численном решении дифференциального уравнения порядка выше первого чаще всего сводится к численному решению решению задачи Коши для нормальной системы дифференциальных уравнений.  Обозначив  y(x)=y₁(x), y'(x)=y₂(x), y''(x)=y₃(x), ..., y^(n-1)(x)=y_n (x),  получим задачу Коши для системы n дифференциальных уравнений 1-го порядка y₁'=y₂ , y₂'=y₃ , ..., y_n' =f(x, y₁, y₂ , ..., y_n ),  y₁(x₀ )=y₀, y₂(x₀)=y_1,0 , ..., y_n-1(x₀)=y_n-1,0,  которая в векторной форме имеет вид `Y '= `F(x,`Y), `Y(x₀) =`Y<sub>0</sub>, `Y (x)=(y₁(x), y₂(x), ..., y_n(x)), `Y '(x)=(y<sub>1</sub>'(x),   y<sub>2</sub>'(x), ..., y<sub>n</sub>'(x)), `F(x,`Y)=  (y₂, y₃, ..., y_n, f(x, y₁, y₂ , ..., y_n )).

Численное решение задачи Коши для этой системы состоит в построении таблицы приближенных значений y_i,1 , y_i,2 , ..., y_i,N компонент y_i(x_j) вектора решения в точках x₁ , x₂ , ..., x_N. Чтобы получить расчетные формулы метода Рунге—Кутты для систем дифференциальных уравнений, достаточно в расчетных формулах для уравнений первого порядка заменить y, f(x, y), k₁, k₂, k₃, k₄ на `Y, `F(x,`Y), `k₁, `k<sub>2</sub>, `k₃, `k₄ .

29. Уравнения, допускающие понижение порядка.  Уравнение вида   решается последовательным n-кратным интегрированием. Пример:    Переобозначив постояные, общее решение запишем в виде y = cos x + C₁x³ + C₂x² + C₃x + C₄.  Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные.

 Порядок уравнения вида F(x, y^(k), y^(k+1), y^(k+2), …,y⁽ⁿ⁾) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y^(k)(x). Тогда   z^(n-k) = y⁽ⁿ⁾(x), и относительно z(x) уравнение примет вид  , т.е. будет уравнением n - k-го порядка. После нахожденияz(x) последовательным интегрированием решается уравнение y^(k) = z(x). 

Уравнение в точных производных.

 Рассмотрим уравнения вида

                                                                                                    

левые части которых являются точными производными от некоторой функции  , т.е.

.

Такие уравнения называются уравнениями в точных производных. Из последнего равенства следует, что соотношение

является первым интегралом уравнения (1) - уравнением (n-1) - го порядка относительно искомой функции. Таким образом, уравнение в точных производных допускают понижение порядка на единицу.

30.Линейные дифференциальные уравнения второго порядка Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид:

, (2.1)

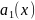где , , и – заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a₀(x) ≠ 0, поделим (2.1) на и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:

(2.2)

Примем без доказательства, что (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям , , если на рассматриваемом промежутке функции , и непрерывны. Если , то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае.

Рассмотрим свойства решений лоду 2-го порядка.

Определение. Линейной комбинацией функций называется выражение , где – произвольные числа.

Теорема. Если и – решение лоду

, (2.3)

то их линейная комбинация также будет решением этого уравнения.

Доказательство.

Поставим выражение в (2.3) и покажем, что в результате получается тождество:

.

Перегруппируем слагаемые:

.

Поскольку функции и являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.

Следствие 1. Из доказанной теоремы вытекает при , что если – решение уравнения (2.3), то тоже есть решение этого уравнения.

Следствие 2. Полагая 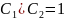, видим, что сумма двух решений лоду также является решением этого уравнения.

Замечание. Доказанное в теореме свойство решений остается справедливым для лоду любого порядка.