- •1. Определение первообразной и её свойства
- •2. Неопределённый интеграл,таблица основных интегралов
- •3. Инвариантность формул интегрирования
- •4.Непосредственное интегрирование
- •5,Интегрирование методом замены переменной(метод подстановки)
- •6. Метод интегрирования по частям
- •7.Примеры интегрирования рациональных функций
- •8 .Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •9.Разложение рациональных функций в сумму простейших дробей
- •10.Интегрирование иррациональных функций
- •14. Определенный интеграл
- •15.Методы вычисления определенного интеграла
- •17. Формула Ньютона Лейбница
- •20. Дифференциальные уравнения первого порядка
- •21. Задача Коши.
- •22.Теорема существования и единственности решения задачи Коши.
- •23. Уравнения с разделяющимися переменными
- •Уравнения вида
- •24. Ду с однородными функциями
- •25.Линейные дифференциальные уравнения первого порядка
- •Преобразованное уравнение является линейным относительно и . Решив его, найдем общий интеграл уравнения Далее, подставив , получим общее решение уравнения Бернулли
- •27.Уравнение в полных дифференциалах
- •Уравнение может быть записано в виде
- •28.Ду высших порядков…..
- •31.Свойства решений лоду
- •32. Определитель Вронского
- •33. Структура общего решения лоду
- •36. Метод вариации произвольных постоянных
- •38.Лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •Вычисление длины дуги плоской кривой
9.Разложение рациональных функций в сумму простейших дробей
Пример 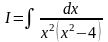 .
.
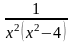 – правильная дробь. Разложим знаменатель
на простейшие сомножители, получим:
– правильная дробь. Разложим знаменатель
на простейшие сомножители, получим:
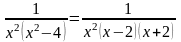 .
.
Корни знаменателя:
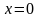 - кратности 2 и
- кратности 2 и
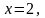
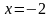 – простые корни.
– простые корни.
Запишем разложение правильной рациональной дроби на сумму простейших:
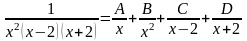 .
.
Приведем дроби к общему знаменателю, затем приравняем числители обеих дробей. Получим тождество:
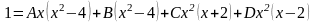 .
.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
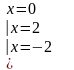
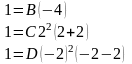 Откуда
Откуда
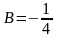 ,
,
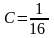 ,
,
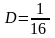 .
.
Чтобы
найти коэффициент
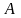 составим уравнение, приравнивая
коэффициенты при
составим уравнение, приравнивая
коэффициенты при
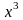 слева и справа в тождестве.
слева и справа в тождестве.
Получим
уравнение: 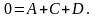 Откуда
Откуда
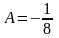 .
.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
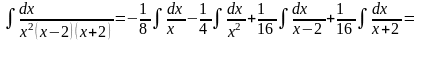
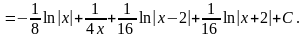
10.Интегрирование иррациональных функций
Функция называется алгебраической иррациональной, если над аргументом производится только четыре арифметических действия и действие возведения в рациональную степень.Метод интегрирования алгебраических иррациональностей состоит в выборе подстановки, которая привела бы подынтегральную функцию к рациональной.Наиболее часто встречаются иррациональности вида:
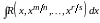 ;
;
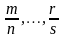 – несократимые дроби.
– несократимые дроби.
Рекомендуется
подстановка:
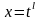 ,
где
,
где
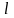 – наименьшее общее кратное знаменателей
дробей (н.о.к.)
– наименьшее общее кратное знаменателей
дробей (н.о.к.)
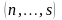 .
.
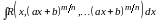 ;
;
Подстановка:
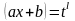 ,
где
,
где
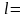 н.о.к.
.
н.о.к.
.
 .
.
Подстановка:
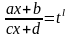 ,
где
н.о.к.
приводит подынтегральную функцию к
рациональному виду.
,
где
н.о.к.
приводит подынтегральную функцию к
рациональному виду.
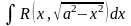 ; Подстановка:
; Подстановка:
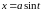 ,
,
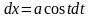 .
.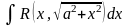 ; Подстановка:
; Подстановка:
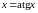 ,
,
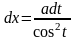 .
.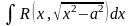 ; Подстановка:
; Подстановка:
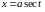 ,
,
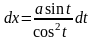 .
.
Рекомендуется подстановка: , где – наименьшее общее кратное знаменателей дробей (н.о.к.) .
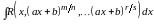 ;
;
Подстановка: , где н.о.к. .
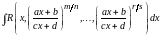 .
.
Подстановка: , где н.о.к. приводит подынтегральную функцию к рациональному виду.
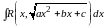 приводится к одному из видов в п. II
методом выделения полного квадрата
трехчлена, стоящего под корнем квадратным.
приводится к одному из видов в п. II
методом выделения полного квадрата
трехчлена, стоящего под корнем квадратным.
12-13. Интегрирование тригонометрических функций
Рассмотрим несколько видов интегралов от тригонометрических функций.
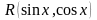 − рациональная функция от
− рациональная функция от
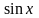 и
и
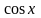 .
Это означает, что над аргументами
производятся только рациональные
операции: сложение, вычитание, умножение,
деление, возведение в целые степени
(положительные и отрицательные). Интегралы
этого вида приводятся к рациональной
функции от
универсальной тригонометрической
подстановкой:
.
Это означает, что над аргументами
производятся только рациональные
операции: сложение, вычитание, умножение,
деление, возведение в целые степени
(положительные и отрицательные). Интегралы
этого вида приводятся к рациональной
функции от
универсальной тригонометрической
подстановкой:
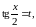
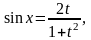
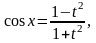
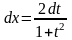 ,
,
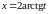 .
.
Следует заметить, что, применяя эту подстановку можно привести любую подынтегральную функцию к рациональной дроби, но иногда получаются громоздкие дроби, которые трудно проинтегрировать.
Рассмотрим частные случаи, когда можно избежать универсальной подстановки.
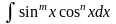 .
.
Где и – целые положительные числа. Если и – четные, то используется тригонометрические формулы понижения степени,
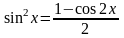 ,
,
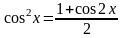 .
.
Пример
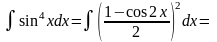
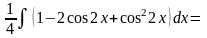
=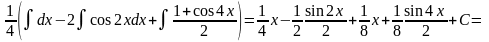
=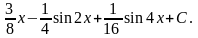
Если одно из чисел или – нечетное, или и – нечетные, то отделяем от нечетной степени один множитель и делаем замену
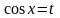 (или
(или
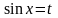 )
–
)
–
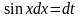 .
.
Пример
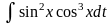 =
=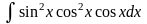 =
=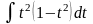 =
=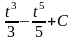 .
.