§ 5. Квантовая модель атома водорода

1. Квантовые числа. Уравнение Шрёдингера в задаче о движении электрона в электрическом поле ядра решается в трёхмерном пространстве в сферической системе координат. Координатами в этой системе являются радиус 0 ≤ r ≤ ∞, полярный угол 0 ≤ θ ≤ π, азимутальный угол 0 ≤ φ ≤ 2π. Решение уравнения Шрёдингера представляет собой произведение трёх функций по трём независимым координатам, , и потому включает в себя три целочисленные параметра – квантовые числа n, l, m. Их названия сложились исторически.

n – главное квантовое число. Оно входит в радиальную часть решения R(r) и определяет уровень энергии. Число n может принимать только целые положительные значения, n = 1, 2, 3, ...

l – азимутальное квантовое число. Оно входит в описание функции Ψ в широтном направлении. Число l может принимать целые положительные значения конечного ряда чисел, l = 0, 1, 2, ... n – 1. Каждому энергетическому уровню с номером n соответствует n значений азимутального квантового числа l.

m – магнитное квантовое число. Оно входит в описание функции Ψ в меридиональном направлении. Число m принимает 2l+1 значений конечного ряда: m = 0, ±1, ±2, ±3, ±... ±l.

Энергия электрона в атоме водорода зависит только от главного квантового числа n. Каждому разрешённому n-му уровню энергии соответствует несколько собственных функций Ψ, отличающихся набором значений квантовых чисел l и m. Это значит, что, будучи на одном и том же энергетическом уровне, атом водорода может находиться в нескольких разных состояниях.

Состояния с одинаковой энергией называются вырожденными, а число разных состояний с одним значением энергии называется кратностью вырождения соответствующего энергетического уровня. Поскольку каждому из n значений квантового числа l соответствует 2l+1 значений квантового числа m, то число разных состояний, соответствующих уровню n, равно

(5.1)

Отсюда следует, что невозбуждённый атом водорода на уровне n = 1 может находиться в одинаково возможном (основном) состоянии. Возбуждённому уровню n = 2 соответствует 2² = 4 возможных состояний, уровню n = 3 – 3² = 9 возможных состояний и т.д.

Часто энергетические уровни обозначают большими буквами латинского алфавита.

n = 1, K-уровень;

n = 2, L-уровень;

n = 3, M-уровень;

n = 4, N-уровень;

n = 5, O-уровень;

n = 6, P-уровень;

n = 7, Q-уровень.

Состояния с разными азимутальными квантовыми числами l обозначают малыми буквами латинского алфавита. Часть этих букв пришла из спектроскопии (первые буквы в названии спектральных серий щелочных металлов).

l = 0, s-подуровень (от англ. sharp – резкий);

l = 1, p-подуровень (от англ. principal – резкий);

l = 2, d-подуровень (от англ. diffuse – размытый);

l = 3, f-подуровень (от англ. fundamental – основной);

l = 4, g-подуровень;

l = 5, h-подуровень.

Обычно состояние электрона в атоме обозначают так:

1s-состояние, n = 1, l = 0.

2s-состояние, n = 2, l = 0.

2p-состояние, n = 2, l = 1.

3d-состояние, n = 3, l = 2, и т.д.

2. Атом водорода в основном состоянии. Главное квантовое число n = 1. Квантовые числа l и m могут принимать единственные значения l = 0 и m = 0. Кратность вырождения n² = 1² = 1. Основное состояние (невозбуждённое) атома водорода единственно возможное.

Функция Ψ представлена лишь радиальной составляющей,

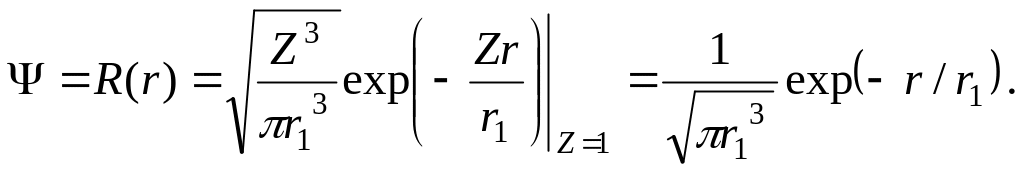(5.1)

Здесь r₁ – боровский радиус, Z = 1 – номер элемента водорода в таблице Менделеева. Но это значит, что также зависит лишь от радиуса r. Электрон с равной вероятностью может быть обнаружен в любой точке сферы определённого радиуса. Говорят, электронное облако имеет центрально-симметричную форму.

На рис. 19 показана зависимость функции Ψ, а на рис. 20 – зависимость функции от расстояния r до ядра. Обе функции убывают монотонно с ростом r, постепенно стремясь к нулю. Поэтому формально не равна нулю вероятность пребывания электрона на сколь угодно больших расстояниях от ядра.

Если в качестве объёма атома брать объём, вероятность пребывания в котором электрона равна единице, то объём атома будет равен бесконечности. Поэтому договорились принимать в качестве объёма атома такой объём, вероятность пребывания в котором электрона составляет 0,9 (90%).

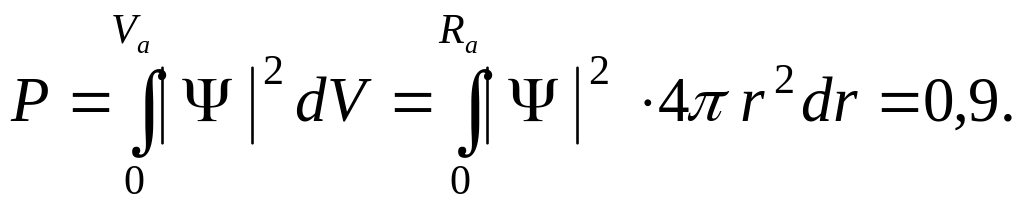(5.2)

Выражение представляет собой элементарный сферический объём, V_a и R_a – объём и радиус шара, вероятность пребывания в котором электрона равна 0,9 (рис. 21).

Из того, что подинтегральная функция не , а следует, что для оценки вероятности пребывания электрона на разных расстояниях r в сферическом облаке более информативна не объёмная плотность вероятности (численно – вероятность в единице объёма), а радиальная плотность вероятности (численно – вероятность в сферическом слое единичной толщины). Хотя функция монотонно убывает, за счёт быстро возрастающего множителя r² выражение в начале растёт и на некотором расстоянии r₁ от ядра обнаруживает максимум (рис. 22). Оказалось, что это расстояние r₁ равно боровскому радиусу атома водорода,  нм.

Но трактовка одного и того же числа r₁ разная. В теории Бора r₁ – это радиус круговой орбиты, на которой электрон находится постоянно. В квантовой теории r₁ – это радиус сферы, вероятность пребывания в окрестности которой у электрона максимальна.

Механический момент у электронного облака в 1s-состоянии равен нулю. Из формулы (4.22)

(5.3)

Магнитный момент электрона в 1s-состоянии также равен нулю. Из формулы (2.18)

(5.4)

[Для сравнения: в атоме Бора моменты не равны нулю. ].

Энергия электрона получается такой же, как и в атоме Бора (ф. 2.13)

Здесь m_e – масса электрона.

3. Возбуждённый атом водорода на энергетическом уровне n = 2. Кратность вырождения 2² = 4.

l = 0. Первое (2s) состояние отчасти повторяет предыдущее состояние 1s. Электронное облако центрально-симметричное. Функции Ψ и имеют более сложный характер (рис. 23 и 24). На расстоянии 2r₁ от ядра функция Ψ имеет узел, то есть обращается в нуль. Сферическая поверхность, соответствующая Ψ = 0, называется узловой. (Функция Ψ в стационарном атоме толкуется как стоячая волна де Бройля. Этим объясняется использование слова «узел»).

Функция имеет два максимума. Слабый максимум на расстоянии r₁ накладывается на максимум 1s-состояния. Сильный максимум находится на расстоянии 4r₁. Графический образ электронного облака в 2s-состоянии показан на рис. 25. Механический и магнитный моменты электрона в 2s-состоянии равны нулю.

l = 1. На p-подуровне электрон может находиться в трёх состояниях, соответствующих m = 0, = ±1.

Если OZ – ось, относительно которой отсчитывается полярный угол θ, а OX – ось, от которой отсчитывается азимутальный угол φ, то электронные облака в 2p-состоянии располагаются, как показано на рис. 26.

В состоянии m = 0 облако напоминает гантель, расположенную вдоль оси OZ. Состояния m = +1 и m = –1 отличаются тем, что функция Ψ имеет в противоположных областях разные знаки. Но квадрат модуля одинаков, Электронное облако в обоих состояниях m = ±1 напоминает тор, образованный вращением знака ∞ (бесконечность) вокруг оси OZ. Оба облака вложены один в другой. На рис. 26 штриховкой показаны сечения изображающих электронные облака тел вращения плоскостью XOZ.

Механический момент электрона в 2p-состоянии не равен нулю.

(5.5)

Проекция механического момента электрона на ось Z может принимать значения:

Здесь m = –1, 0, +1 – квантовое число.

Магнитный момент электрона в 2p-состоянии

(5.6)

Проекции магнитного момента электрона на ось Z могут принимать значения

Здесь m_e – масса электрона.

4. Возбуждённый атом водорода на энергетическом уровне n = 3. Кратность вырождения 3² = 9.

l = 0. Электронное облако в 3s-состоянии центрально-симметричное. График радиальной плотности вероятности для 3s-электрона показан на рис. 27. Максимумы кривой приходятся примерно на радиусы боровских орбит r₁ 4r₁ 9r₁. Две сферические узловые поверхности имеют приблизительно радиусы 2r₁ и 7r₁.

Механический и магнитный моменты 3s-электрона равны нулю.

l = 1. Форма облаков в 3p-состоянии примерно такая же, как и в 2p-состоянии (рис. 26). Но радиальная плотность вероятности меняется. Появляется одна узловая поверхность – сфера с радиусом 6r₁ (рис. 28). Поэтому при m = 0 «гантель» распадается на две области: малую область внутри этой сферы и «гантель» вне этой сферы.

При m = ±1 тор также распадается на две области. Маленький тор находится внутри сферы радиуса r = 6r₁, большой – снаружи!

Механический L и магнитный p_m моменты электрона в 3p-состоянии такие же, как и в 2p-состоянии (формулы 5.5 и 5.6).

l = 2. Форма облаков в 3d-состоянии скромнее. Их конфигурации и сечения показаны на рис. 29.

Облака в 3d-состоянии на имеют узловых поверхностей.

С дальнейшим ростом главного квантового числа n s-состояние всегда остаётся центрально-симметричным. Общая конфигурация электронных облаков в p, d, f ... состояниях в основном исчерпывается фигурами рис. 29.

5. Опыты Штерна и Герлаха. Улучшение разрешающей способности спектральных аппаратов привело к началу 20-х годов к появлению проблемы, не находившей своего объяснения. Спектроскописты открыли тонкую структуру спектральных линий. Многие линии, которые при слабом разрешении считались одиночными (синглеты), при сильном разрешении оказались двойными (дублеты), тройными (триплеты) и даже с большим числом линий (мультиплеты).

К этому времени (1921 г.) была основательно разработана теория Бора. Естественно, что с её помощью пытались объяснить в первую очередь спектры щелочных металлов, атомы которых были наиболее «водородоподобны». В центре атома щелочного металла находится остов – ион с зарядом +e, а вокруг этого иона движется слабо связанный с ним электрон.

Объяснить спектральные дублеты щелочных металлов можно было тем, что орбитальный магнитный момент электрона взаимодействует с магнитным моментом остова. Поэтому возник вопрос: действительно ли водородоподобные атомы имеют магнитный момент и если да, то квантован ли он?

В 1921 г. немцы Отто Штерн и Вальтер Герлах в прямых опытах доказали, что атомы имеют магнитный момент и что магнитный момент атомов квантован.

В сосуде с высоким вакуумом с помощью диафрагм В создавался узкий атомный пучок элемента, испарявшегося в печи К (рис. 30). Пучок проходит через сильно неоднородное магнитное поле между полюсами N и S магнита.

Один из наконечников (N) имел вид призмы с острым ребром, а вдоль другого (S) была выточена канавка. После прохождения магнитного поля пучок оставлял след на фотопластинке P.

Идея опыта была в том, что если атомы в пучке имеют магнитный момент, то в магнитном поле они должны вести себя как маленькие магнитики. В однородном магнитном поле на магнит действует вращающий момент, поэтому магнитный атом может изменять свою ориентацию. В неоднородном поле кроме момента на магнит действует ещё сила, при одной ориентации втягивающая его к ребру (в область большей магнитной индукции), при другой – к канавке (в область меньшей индукции). (См. Электричество, §14).

Если магнитного поля нет, то на пластинке Р должна получаться узкая полоска осаждённых атомов. Если поле есть, а атом ведёт себя как классический маленький маятник со случайной ориентацией магнитного момента, то полоска на пластинке Р должна уширяться, оставаясь сплошной. Если же магнитный момент атома квантован, то полоска должна расщепляться на несколько полос в зависимости от числа квантовых состояний.

Опыты проводились с атомами серебра Ag, водорода Н, лития Li и других щелочных металлов. Оказалось, что в случае атомов 1-й группы (Li, H, Ag) полоска расщеплялась на две симметрично расположенные полоски. Это говорит о том, что атомы 1-й группы имеют магнитный момент и способны принимать две ориентации – по полю и против поля.

В теории Бора это можно было объяснить наличием орбитального магнитного момента внешних электронов. Тем более вычисления показали, что магнитный момент атома водорода в опытах Штерна равен магнетону Бора. Но буквально через 3-4 года, когда на смену теории Бора пришла квантовая механика, стало ясно, что никакого расщепления атомы водорода и щелочных металлов давать не должны. По анализу Паули, сделанному в 1923 г., следовало, что магнитные моменты остовов атомов щелочных металлов равны нулю. А из решения уравнения Шрёдингера, полученного через три года, получалось, что внешний электрон в атомах водорода и щелочных металлов находится в s-состоянии, и его магнитный момент так же равен нулю. Откуда же взялся магнитный момент атомов в опытах Штерна?

6. Спин. В 1925 г. ответили на этот вопрос американцы Сэмюэль Гаудсмит и Джордж Юленбек. Они показали, что дублеты в спектрах и опыты Штерна и Герлаха можно объяснить, если предположить существование у электронов собственного механического и магнитного моментов. Идея спина оказалась очень плодотворной и быстро нашла признание.

В начале полагали, что спин электрона обусловлен его вращением вокруг собственной оси. (Отсюда название от английского to spir – вращаться). Но расчёты показали, что линейная скорость движения поверхности шарика-электрона в несколько раз должна превышать скорость света. Поэтому пришлось отказаться от столь наглядного толкования.

В настоящее время словом «спин» обозначают собственный механический момент элементарных частиц, имеющий квантовую природу. Спин задаёт пространственную ориентацию частицы.

Для определения состояния микрочастицы к трём квантовым числам n, l, m нужно добавить ещё одно – спиновое квантовое число s. Оказалось, что у электрона спиновое число может принимать только два значения, s = +1/2 и s = –1/2.

Собственный (спиновый) механический момент электрона может иметь лишь одно единственное значение (см. ф. 4.22).

(5.7)

Проекция механического момента электрона на физическую ось z (например, линии магнитного поля в опытах Штерна) может принимать два значения (см. ф. 4.23).

(5.8)

Это в 2 раза меньше минимального значения.

Из формулы (2.18) следует, что отношение орбитального магнитного момента М электрона к механическому L равно

Орбитальное гиромагнитное отношение (5.9)

Опыт показывает, что спиновое гиромагнитное отношение в 2 раза больше.

Спиновое гиромагнитное отношение (5.10)

Отсюда спиновый магнитный момент электрона (5.11)

Появление 4-го квантового числа s (спинового) увеличивает число состояний электрона на n-ном энергетическом уровне. Поскольку спиновое квантовое число s может принимать только два значения, то и число максимально возможных состояний электрона увеличивается в 2 раза и равно 2π².

Таким образом, в 1s-состоянии, например, максимальное число электронов не один ,а два. В одном и том же центрально-симметричном облаке могут находиться в 1s-состоянии два электрона с противоположными спинами.

7. Излучение и поглощение света атомом водорода. Как и в теории Бора, излучение и поглощение света атомом квантовая механика связывает с переходами электрона с одного энергетического уровня на другой. Из дискретности энергетических уровней вытекает линейчатая структура спектров.

Опыт и теория показывают, что могут реализовываться не любые переходы электрона в атоме. Возможность перехода определяется правилами Бора. Их два.

Для азимутального квантового числа l. (5.12)

Для магнитного квантового числа m. (5.13)

Что касается вероятности переходов электрона с одного уровня на другой, то решение уравнения Шрёдингера для электрона в центральном поле ядра не даёт ответа на этот вопрос. Все уровни представляются в смысле устойчивости равноценными. На каждом уровне электрон может находиться сколь угодно долго. Поэтому разные интенсивности спектральных линий не объясняются.

Для объяснения самопроизвольных переходов электрона нужно кроме электрона в поле ядра учитывать одновременно и поле излучения. То есть решать задачу для системы, состоящей из атома и поля излучения. Такая квантовая теория излучения была построена в первой трети 20 века. Она смогла объяснить не только интенсивность спектральных линий, но и поляризованность излучения.

На рис. 31 показана схема уровней энергии атома водорода и разрешённые пути перехода. Толщина линий соответствует вероятности перехода. В соответствии с правилом отбора по азимутальному квантовому числу запрещены переходы между одноимёнными подуровнями типа 2s → 1s, 3p → 2p, 4d → 3d и так далее. Поэтому на рисунке все линии переходов косые (прямые линии объединяют одноимённые подуровни).

Слева на рисунке показана энергия возбуждения атома в электронвольтах, отсчитываемая от основного 1s-состояния. Длина волны на рисунке указана в ангстрёмах, нм.