Численные методы Сизихина Ольга Викторовна

План курса

План курса 1

Методы численного интегрирования 1

Общая схема численного интегрирования: 2

Формулы прямоугольников 2

Формула трапеций 4

Формула парабол (Симпсона) 5

Интерполяция функций 6

Метод Лагранжа 7

Метод Ньютона 8

Обработка данных эксперимента. Построение эмпирической зависимости 8

Методы численного интегрирования

При решении многих практических задач встает проблема вычисления определенного интеграла , где – некоторая интегрируемая на отрезке функция.

Из курса интегрального исчисления функции одной переменной известна формула Ньютона–Лейбница: если функция непрерывна на отрезке , то для нее существует первообразная на этом отрезке и .

Эта формула представляет собой точный метод вычисления определенного интеграла. Однако в реальности использовать ее удается не всегда. Она теряет свой практический смысл в следующих ситуациях:

• «неберущийся» интеграл, т.е. первообразная 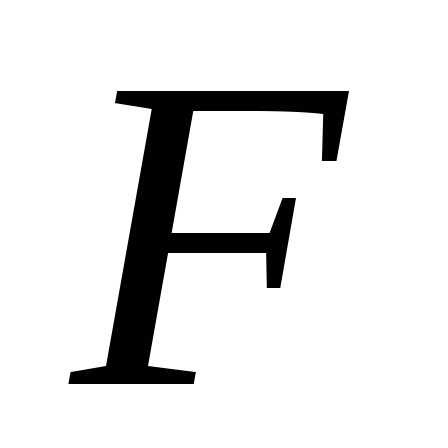не выражается через элементарные функции. Пример: , ;

• первообразная существует, но ее отыскание требует сложных преобразований;

• подынтегральная функция задана таблично, и при этом неизвестно ее аналитическое выражение.

Во всех указанных случаях применяют методы численного интегрирования.

Численное интегрирование – это вычисление определенного интеграла по ряду числовых значений функции .

Методы численного интегрирования можно разделить на аналитические и собственно численные. Суть аналитических методов состоит в замене подынтегральной функции на отрезке некоторой аналитически заданной функцией, чью первообразную найти нетрудно. Наиболее часто функцию заменяют интерполяционным многочленом или функцией, полученной по методу наименьших квадратов (см. тему «Обработка данных эксперимента»). Собственно численные методы позволяют обходиться без дополнительных аналитических построений. Определенный интеграл вычисляется только по ряду табличных значений функции.

Общая схема численного интегрирования:

Отрезок интегрирования разбивается на частей. На каждом частичном отрезке некоторым образом выбирается точка , вычисляется значение функции в этой точке и составляется расчетная формула .

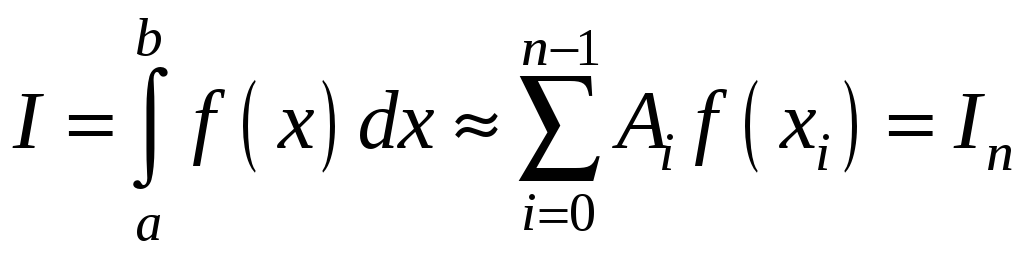Формулы такого вида получили название квадратурных формул. В случае, когда частичные отрезки имеют одинаковую длину (таблица с равноотстоящими узлами), говорят о квадратурных формулах Ньютона–Котеса. Числовые коэффициенты определяются методом интегрирования.

Остаточный член таков, что . Это означает, что чем меньше шаг разбиения, тем квадратурная формула точнее, и, следовательно, достаточно мелким разбиением отрезка интегрирования можно обеспечить сколь угодно малую погрешность квадратурных формул.

Наибольшее распространение получили 3 вида квадратурных формул: формулы прямоугольников, трапеций и парабол (Симпсона).

Формулы прямоугольников

Разобьем отрезок интегрирования на равных частей с шагом . Получаем последовательность точек , где . Тогда по свойству аддитивности определенного интеграла .

На каждом частичном отрезке заменим подынтегральную функцию многочленом нулевой степени. Например, на отрезке . Тогда и . Эта формула называется формулой левых прямоугольников. Можно заменить на частичном отрезке подынтегральную функцию ее значением в правом конце отрезка, т.е. . Тогда и . Эта формула получила название правых прямоугольников. Более точной формула численного интегрирования будет, если заменить подынтегральную функцию ее значением в середине отрезка: . Тогда и получаем формулу центральных прямоугольников: .

Пример 1: вычислить значение определенного интеграла по формулам прямоугольников с разбиением отрезка интегрирования на 4 отрезка.

Решение:

1. Составим таблицу значений функции. Шаг таблицы

   n	0	1	2	3	4
   x	0	0,5	1	1,5	2
   y	0	0,25	1	2,25	4

2. По формуле левых прямоугольников:

.

3. По формуле правых прямоугольников:

.

4. По формуле центральных прямоугольников:

n	0		1		2		3		4
x	0	0,25	0,5	0,75	1	1,25	1,5	1,75	2
y	0	0,0625	0,25	0,5625	1	1,5625	2,25	3,0625	4

.

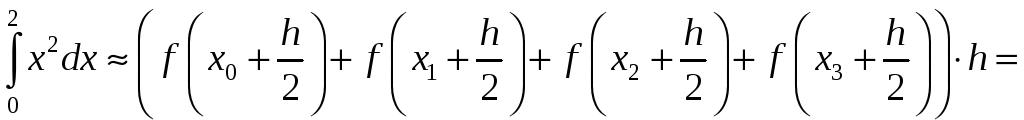
Оценить погрешность интегрирования можно по формуле , где . Таким образом, погрешность обратно пропорциональна n, т.е. чем больше n, тем меньше погрешность.

Оценим погрешность вычисления интеграла из примера 1 методом центральных прямоугольников: , , . Тогда – абсолютная погрешность и .