§18. Проблема строения атомного ядра

1. Открытие протона. В 1919 г. Эрнст Резерфорд впервые осуществил искусственное превращение ядер азота. Схема установки показана на рис. 132. Альфа-активный препарат полоний наносился на держатель Д внутри кюветы К. Сцинтилляции α-частиц могли наблюдаться на стеклянной пластинке Пл с порошком ZnS через микроскоп М.

Альфа-частицы имеют энергию 7,58 МэВ и длину пробега в воздухе при нормальном давлении около 7 см. Держатель Д был установлен на таком расстоянии от пластинки Пл, что при пониженном давлении газа в кювете α-чатисцы могли доходить до пластинки Пл и вызывать на ней сцинтилляции. При нормальном и повышенном давлении α-частицы до пластинки Пл не доходили.

Кювета заполнялась разными газами, после чего наблюдались сцинтилляции α-частиц при малых давлениях и их исчезновение с ростом давления.

При заполнении кюветы азотом N₂ на пластинке Пл наблюдались сцинтилляции и при давлениях, больших предельного. Поскольку α-частицы не могли дойти до люминофора, оставалось сделать предположение, что в процессе взаимодействия α-частиц с ядрами азота рождались какие-то другие ионизирующие частицы.

Наложение электрического и магнитного полей позволили установить, что рождающаяся новая частица имеет положительный заряд, равный по абсолютной величине заряду электрона, и массу, приблизительно равную массе водорода. Очевидно, это ядро атома водорода, как α-частица – ядро атома гелия.

Ещё в 1910-х годах была высказана идея, что ядра всех химических элементов состоят из ядер водорода – то есть ядер простейшего, первого в таблице элемента. Поэтому Резерфорд назвал новую частицу «протон», образовав это слово от греч. protos – первый. (Ещё раньше, в 1815 г., подобную идею в отношении состава химических элементов высказал химик Уильям Праут).

Патрик Блэкетт продолжил в 1925 г. опыты с азотом с помощью усовершенствованной им камеры Вильсона (см. с. ). Он автоматизировал съёмку туманных треков ионизирующих частиц двумя фотокамерами одновременно с разных направлений. Это позволило восстановить пространственную форму траекторий частиц. Сделав 23 000 снимков и посмотрев их, он установил, что α-частица при столкновении поглощается ядром азота, после чего это новое ядро выбрасывает протон. С учётом сохранения заряда и массы ядерная реакция может быть записана так:

Резерфорд, 1919 г. Открытие протона (18.1)

Энергия протонов в опытах Резерфорда составляла около 6 МэВ, а длина пробега 28 см.

2. Свойства протона. Протон в свободном состоянии – стабильная элементарная частица, ядро атома водорода. В ядерных реакциях обозначается часто символом . Масса протона m_p почти в 2000 раз превышает массу электрона m_e, m_p = 1836 m_e = 1,67239 · 10^–27 кг.

Спин, то есть собственный момент импульса протона такой же, как у электрона. Его проекция на физическую ось может принимать только два значения, . Спиновое квантовое число s протона, как и у электрона, полуцелое, . Поэтому система протонов, как и система электронов, описывается статистикой Ферми-Дирака.

Магнитный спиновый момент протона. Как уже говорилось в §2, в теории атома водорода Бора орбитальный магнитный момент электрона в низшем энергетическом состоянии (n = 1) равен  Дж/Тл (см. ф. 2.18). На более высоком энергетическом уровне магнитный момент в n раз больше, где n – номер уровня, M_n = n · M₁. Минимальную величину магнитного момента называют магнетоном Бора. Это минимальный магнитный момент в физике электронных оболочек атомов. Поэтому магнетон Бора используется в качестве системы измерений магнитных моментов электронов.

Из опытов Штерна и Герлаха по расщеплению атомных пучков в неоднородном магнитном поле следовало, что спиновый магнитный момент электрона равен магнетону Бора. Поэтому после открытия протона было естественным предположение, что спиновый магнитный момент протона определяется формулой магнетона Бора, в которой вместо массы электрона m_e должна стоять масса протона m_p.

 Дж/Тл. (18.2)

Величину М_я называют ядерным магнетоном. Он в 1836 раз меньше магнетона Бора и используется в качестве единицы измерения магнитных моментов в ядерной физике.

Но измерения показали, что спиновый магнитный момент протона больше магнетона Бора в 2,79 раз и составляет

 Дж/Тл. (18.3)

3. Ядерные реакции с испусканием протона наблюдались позднее при обстреле α-частицами бора , фтора , натрия , алюминия и фосфора .

Заметим, что α-частицы могут результативно взаимодействовать лишь с лёгкими ядрами. Чтобы преодолеть электрическое отталкивание ядра, α-частица должна иметь кинетическую энергию Е, не меньшую потенциальной энергии необходимого для протекания реакции сближения с ядром.

(18.4)

Отсюда можно найти максимальный номер Z элемента, ядро которого доступно для α-частицы с энергией Е.

. (18.5)

Радиус ядра  м. Для α-частиц с энергией Е ≈ 10 МэВ получаем

Это завышенное число. Как показывают опыты, эффективное взаимодействие α-частиц с ядрами реально лишь для элементов с Z ≤ 20, то есть до кальция.

4. Открытие нейтрона. К 1930 г. выяснилось, что некоторые элементы, например, Be, Li, O₂ при обстреле α-частицами протонов не испускают. Поэтому возник вопрос: что же происходит в тех случаях, когда обстреливаемое α-частицами ядро не выбрасывает протон?

В 1930 г. Вальтер Ботс и Г. Бекер поставили опыт, схема которого показана на рис. 133. На держателе Д помещался α-активный препарат . Его особенность в том, что испытав α-распад полония –210 превращается в ядро стабильного изотопа свинца . Поэтому никаких других излучений препарат полония –210 не даёт. Энергия α-частиц у меньше, чем у , она составляет 5,25 МэВ. Но для проникновения в ядра выбранного для опытов лёгкого бериллия, у которого Z = 4, этого было достаточно.

Было опасение, что ядра, не испускающие протоны, испускают другое излучение, не дающее вспышек в сернистом цинке ZnS. Поэтому экран из сернистого цинка был заменён счётчиком Гейгера. Его действие основано на том, что ядерная частица, влетающая внутрь счётчика, ионизирует находящийся в нём газ. В результате в цепи счётчика возникает импульс тока (подробнее см. с. ).

Опыт показал, что при облучении α-частицами пластинок из бериллия , бора , лития возникает какое-то излучение, вызывающее слабые разряды счётчика Гейгера. Особенно сильное излучение давал бериллий. Эти бериллиевые лучи обладали огромным проникающим действием: пластина свинца толщиной 2 см уменьшала их интенсивность всего на 14%. Боте и Бекер предположили, что бериллиевые лучи представляют собой очень жёсткие γ-кванты. По поглощению в свинце было найдено, что энергия бериллиевых γ-квантов составляет 7 МэВ. Но энергия α-частиц составляла 5,25 МэВ. откуда же взялся прирост энергии?

В 1931 г. к исследованиям бериллиевых лучей присоединились Ирен и Фредерик Жолио-Кюри. Помещая вместо свинцовых пластин листы парафина, они обнаружили, что из парафина под действием бериллиевых лучей исходили протоны, максимальный пробег в воздухе которых составлял 26 см. Такому пробегу соответствовала энергия протона 4,5 МэВ.

Парафины – это насыщенные углеводороды с общей формулой С_nH_2n+2. В них большое число атомов водорода. Появление протонов при облучении парафина бериллиевыми лучами упруги Кюри истолковали как результат комптоновского рассеяния γ­-квантов на протонах – ядрах атомов водорода. Протон отдачи уходит вперёд, когда рассеянный γ-квант отражается назад, θ = π. Отсюда где m_p – масса протона, λ₀ – длина волны бериллиевых γ-квантов.

Энергия Е выбитого протона должна быть равной убыли энергии γ-кванта,

(18.6)

Допустим для оценки, что

Тогда

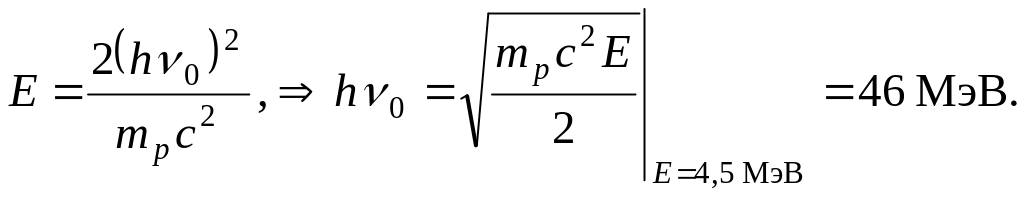
Итак, энергия бериллиевых γ-квантов, вычисленная по поглощению в свинце, 7 МэВ, по энергии выбитых из парафина протонов – 46-48 МэВ. Кроме того получается, что α-частицы с энергией 5,25 МэВ выбивает γ-квант с энергией 46-48 МэВ!

В 1932 г. в исследования природы бериллиевых лучей включается Джеймс Чедвик. Схема его установки практически ничем не отличалась от схемы Боте и Бекера, только вместо счётчика Гейгера он, как и Кюри, использовал ионизационную камеру.

Чедвик исследовал рассеяние бериллиевых лучей не только парафином, но и другими веществами. Энергия γ-квантов, измеренная по энергии ядер отдачи азота оказалась равной hν = 150 МэВ.

Итак, гипотеза, согласно которой бериллиевые лучи есть γ-кванты, приводила к противоречивым результатам. В зависимости от метода измерения энергия γ-квантов получалась разной и составляла 7, 48, 80, 150 МэВ. Это доказывало направленность данной гипотезы.

В том же 1932 г. Чедвик пришёл к выводу, что бериллиевое излучение есть поток нейтральных частиц, которые он назвал нейтронами. Обозначают нейтроны символом . Ядерную реакцию рождения нейтронов можно записать так:

Реакция открытия нейтронов, 1930-32 г. (18.7)

Чедвик выполнил и первые измерения массы нейтрона. Оказалось, что масса нейтрона близка к массе протона. Точное значение массы нейтрона было получено из баланса масс различных ядерных реакций с участием нейтронов.

5. Свойства нейтрона. Нейтрон в свободном состоянии – нестабильная элементарная частица, распадающаяся на протон, электрон и электронное антинейтрино.

(18.8)

Среднее время жизни нейтрона τ ≈ 16 минут.

Масса нейтрона несколько больше массы протона и составляет m_n­­ = 1838 m_e =  1,6760 · 10^–27 кг. Спин нейтрона такой же, как у протона и составляет ħ/2. Поэтому нейтроны, как электроны и протоны, описываются статистикой Ферми-Дирака.

Хотя «минус» означает, что направления собственных механического и магнитного моментов нейтрона противоположны. Отношение спиновых магнитных моментов протона и нейтрона составляет M_p/M_n = –3/2.

Высокая проникающая способность нейтронов объясняется отсутствием у них электрического заряда. Нейтроны практически не взаимодействуют с электронными оболочками атомов и в отличие от α-частиц и протонов не отталкиваются от ядер. Поэтому даже при малых энергиях нейтроны могут вплотную подходить к атомным ядрам и захватываться ими.

Для регистрации быстрых нейтронов используют их упругие столкновения с ядрами водорода. Благодаря практическому равенству масс протона и нейтрона при упругом ударе нейтрона с неподвижным протоном последнему передаётся большая часть кинетической энергии нейтрона. В результате нейтрон практически останавливается, а протон движется в том же направлении с энергией, близкой к первоначальной энергии нейтрона. По пути протон производит интенсивную ионизацию и потому может регистрироваться ионизационной камерой, счётчиком Гейгера или камерой Вильсона.

После нескольких последовательных столкновений с атомными ядрами быстрые нейтроны отдают свою избыточную энергию и в дальнейшем совершают хаотическое движение с тепловыми скоростями. Для таких тепловых нейтронов описанный выше метод регистрации путём рассеяния на ядрах атомов водорода непригоден. В этом случае используют ядерные реакции, при которых нейтрон, проникая в яро, приводит к вылету из последнего α-частицы большой энергии. Например,

(18.10)

6. Проблема строения ядра. К началу 30-х годов 20 в. были открыты следующие структурные элементы атома: электрон, 1897 г., Томсон; протон, 1919 г., Резерфорд; нейтрон, 1932 г., Чедвик. открытие радиоактивности и наблюдение первых ядерных реакций сделали актуальным вопрос: как устроено атомное ядро?

Прежде всего стало очевидно, что ядро атома нельзя представлять в виде шара, сложенного из неких неподвижных ядерных кирпичей. Ядро атома – это очень малый объём пространства, в котором движутся ядерные элементы. то есть это система ядерных объектов, движущихся и взаимодействующих по каким-то специфическим, пока ещё неизвестным законам.

В первую очередь надо было ответить на вопрос: из каких частиц состоит ядро. Исторически были рассмотрены два варианта: протон-электронное и протон-нейтронное ядро.

а. Протон-электронное ядро. Ещё до открытия нейтрона в 1930 г. Поль Дирак проанализировал идею Праута о том, что все химические элементы состоят из водорода. Применительно к проблеме строения ядра эта идея сводилась к тому, что все ядра элементов состоят из ядер атома водорода, то есть из протонов. (Изотоп водорода дейтерий был открыт только через 2 года). Но это значит, что порядковый номер элемента в таблице Менделеева должен быть равен его массовому числу. Но таких элементов в таблице нет. Уже у гелия порядковый номер Z = 2, а массовое число А = 4. Как будто из 4-х протонов в ядре 2 нейтрализованы.

Можно предположить, что ядро гелия содержит 4 протона и 2 электрона. Но в этом случае появляются противоречия с принципом неопределённости Гейзенберга. Действительно, неопределённость импульса в ядре, выраженная из соотношения неопределённости для координаты-импульса есть:

(18.11)

Но неопределённость координаты Δх не может быть больше радиуса ядра, по крайней мере Δх ≈ r₀. Из опытов Резерфорда 1909 г. r₀ ≈ 10^–15 м. импульс электрона в ядре не может быть меньше неопределённости импульса, а его минимальная скорость движения в ядре из релятивисткой формулы.

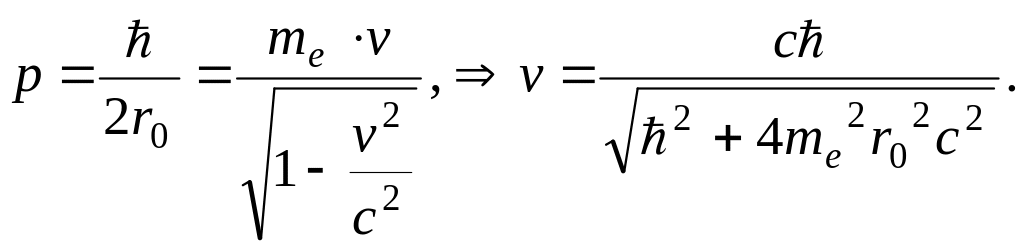(18.12)

Здесь m_e – масса покоя электрона. После вычислений получаем v = 0,99998c, где с – скорость света.

Вычисленная по релятивистской формуле кинетическая энергия электрона в ядре составляет

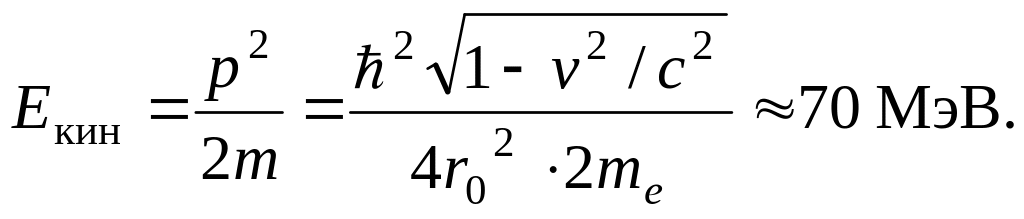
Но электроны, вылетающие из ядра при β-распаде, имеют энергию в пределах 10 МэВ. Столь разительному несоответствию очень трудно найти убедительное объяснение.

Вторая трудность протон-электронной модели ядра носит название азотной катастрофы. Суть её в следующем.

По величине сверхтонкого расщепления атомных спектров удалось вычислить магнитный момент атомных ядер. Он оказался примерно в 1000 раз меньше спинового магнитного момента электрона. Если в ядре чётное число электронов, то столь малый, магнитный момент ядра можно объяснить тем, что электроны в ядре образуют пары с противоположными спинами, поэтому магнитный момент ядра складывается из моментов протонов. А магнитный момент протона в 658 раз меньше момента электрона.

Но в ядре атома азота должно быть 14 протонов и 7 электронов. Если 6 электронов образуют пары с противоположными спинами, то один электрон остаётся неспаренным. Этот неспаренный электрон должен обеспечить ядру азота такой же магнитный момент, какой он имеет, то есть в 1000 раз больше, чем у ядер с чётным числом электронов. Но этого нет. Магнитный момент ядра азота того же порядка, что и у других ядер.

б. Протон-нейтронное ядро. Менее чем через полгода после открытия нейтрона практически одновременно и независимо друг от друга Дмитрий Иваненко и Вернер Гейзенберг предложили протон-нейтронный состав ядра. Разработанная позднее протон-нейтронная модель ядра прекрасно соответствует эксперименту и является сейчас общепринятой.

Согласно этой модели ядро атома содержит Z протонов A–Z нейтронов. Здесь Z – порядковый номер элемента в таблице Менделеева. Заряд ядра q = Ze₊, поэтому номер Z называют часто зарядовым числом. Величину А называют массовым числом. Это целое число, равное атомной массе элемента, выраженной в углеродных единицах и округлённой до целого числа.

Протоны и нейтроны, находящиеся в составе ядра, называют нуклонами (от лат. nucleus – ядро). Тем самым подчёркивается, что протон и нейтрон в составе ядра – это одна и та же частица в разных состояниях. Массовое число А есть число нуклонов в ядре. В зависимости от соотношения между количествами протонов и нейтронов в ядрах различают изотопы, изобары и изотоны.

Изотопы (от греч. isos – равный, topos –место) – ядра, содержащие одинаковое количество протонов, то есть имеющие одинаковое количество протонов, то есть имеющие одинаковый номер Z, и разное число нейтронов. Все изотопы помещаются в одной клетке таблицы Менделеева и являются разновидностями одного химического элемента. Различаются изотопы числом N нейтронов в ядре. Например, изотопы водорода:

Протий, , ядро-протон, Z = 1, A = 1, N = A–Z = a, нейтронов нет.

Дейтерий, , ядро-дейтрон, Z = 1, A = 2, N = 1, один нейтрон.

Тритий, , ядро-тритон, Z = 1, A = 3, N = 2, два нейтрона.

Изотопы гелия:

, Z = 2 (два протона), A = 3, N = 1 (один нейтрон), стабилен.

, Z = 2, A = 4, N = 2 (два нейтрона), стабилен.

, Z = 2, A = 6, N = 4 (четыре нейтрона), нестабилен.

, Z = 2, A = 8, N = 6 (шесть нейтронов), нестабилен.

У известных ныне элементов число Z достигает примерно значения 105. На это число элементов приходится примерно 1500 известных изотопов. В среднем на один элемент – 14 изотопов. Из них 1/5 – стабильных и 4/5 – нестабильных.

Изотопы одного химического имеют одинаковые химические и почти одинаковые физические свойства. Поэтому разделение изотопов – сложная физико-химическая задача. Наиболее заметно различаются изотопы водорода.

Изобары (от изос- и греч. baros – тяжесть) – ядра с одинаковым массовым числом А. Например, тритий и гелий . У них по 3 нуклона, но соотношение между протонами и нейтронами разное. У трития Z = 1, N = 2, у гелия Z = 2, N = 1.

Изотоны – ядра с одинаковым числом нейтронов. Как и изобары, изотоны – это ядра разных химических элементов. Например, ядра разных содержат по 3 нейтрона.

Слова изобары и изотоны используются много реже, чем слово изотопы.