Пространственная и временная когерентность световых волн

Временная когерентность. Любая световая волна является наложением колебаний всевозможных частот. Даже для света, который считается монохроматическим, колебания заключены в конечном интервале частот (или ). Кроме того, фаза и амплитуда испытывают случайные (хаотические) изменения. Поэтому в общем случае волна описывается уравнением

Посчитаем для простоты, что А не зависит от t . Введем среднее значение частоты - относительно которого происходят изменения . Тогда фазу можем записать в виде

Обозначим через .

То есть мы получили функцию, у которой хаотические изменения претерпевает лишь фаза. Если происходит сложение двух волн с преобразованными, как сделано выше, фазами, то результирующая интенсивность, как известно из (3.1)’, будет зависеть от .

то есть - разность фаз будет не постоянной, а зависеть от времени.

Если за время срабатывания прибора (глаз ~ 0.1 с) t_приб. Значения менялись от +1 до –1, то интерферентную картину не зарегистрируем и . Если за время t_приб., то волны будем считать когерентными, и интерф. картина регистрируется. Можно ввести время когерентности. Это время t_ког., за которое случайное изменение фазы достигает значения . При постоянной времени прибора

t_приб>> t_ког – интерфер. картина на наблюдается,

t_приб<< t_ког – наблюдается. (3.6)

Расстояние , на которое смещается волна за время t_ко, называется длиной когерентности. Расстояние, на которое фаза меняется на ~.

При разности хода лучей - интерфер. картина наблюдается (для разделенных волн).

Пространственная когерентность

Временная когерентность определяется разбросом значений частот и соответственно значений модуля волнового вектора (так как ).

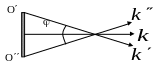Пространственная когерентность обусловлена разбросом направлений вектора из-за наличия протяженного источника света. Рассмотрим на примере диска. Угол , под которым виден диск в данной точке и характеризует разброс напр-ий вектора . (Считаем, что временная когерентность достаточная для получения четкой интерференции картины).

Если излучение от диска падает на две щели, то волны идущие по направлению создают первый максимум выше на , чем по направлению волны .

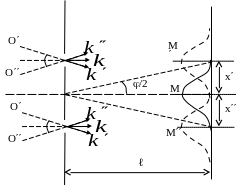Смещение будет меньше, чем ширина интерф. полосы , то максимумы практически наложатся друг на друга и источник можно считать точечным. Интереферентная картина наблюдается. Если ~ максимумы наложатся на соседние минимумы и интерф-ой картины не наблюдается. Т.о. интерфер. картина наблюдается при условии < или

Это условие можно записать для расстояния между щелями

(3.7)

При уменьшении d – расстояния между щелями или точками волновой поверхности можно добиться соблюдения (3.7). Колебания между точками монохроматической волновой поверхности можно считать когерентными, если расстояние между ними меньше - называется радиусом когерентности . Лазер обладает большой пространственной и временной когерентностью. Томас Юнг в 1802 году увеличил пространственную когерентность, пропустив свет сначала через одно отверстие в ширме, а потом через два – в другой ширме.

При увеличении расстояния от источника , то есть пространственная когерентность увеличивается.