7.2. Представление эдс индукции с помощью теоремы Стокса

В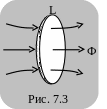 озникновение индукционного тока в контуре свидетельствует о том, что при изменении магнитного потока через поверхность, ограниченную контуром (рис. 7.3), возникают сторонние силы и электроны движутся в поле с напряженностью . При этом ЭДС электромагнитной индукции

.

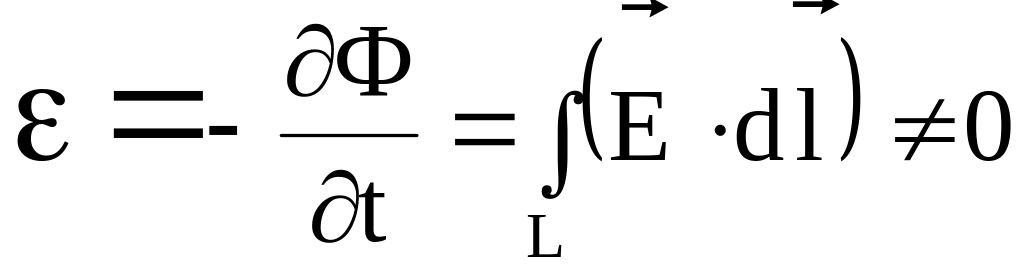И звестно, что теорема Стокса позволяет, выразить криволинейный интеграл через поверхностный интеграл. Если - поверхность, ограниченная замкнутым контуром , и рассматриваемый вектор является функцией трех переменных x, y, z (рис. 7.4), то имеет место утверждение: циркуляция вектора напряженности электрического поля по замкнутому контуру равна потоку ротации через любую поверхность , ограниченную контуром . Математически это утверждение можно записать так:

. (7.14)

Для рассматриваемого случая имеем

(7.15).

Следовательно,

.

Откуда

. (7.16).

Полученное математическое выражение закона электромагнитной индукции (7.16) известно как одно из уравнений Максвелла в дифференциальной форме.

7.3. Представление циркуляции с помощью теоремы Стокса

С помощью теоремы Стокса можно преобразовать теорему о циркуляции вектора напряженности магнитного поля .

Известно, что математически теорема о циркуляции вектора напряженности магнитного поля может быть записана так:

или

. (7.17)

С помощью теоремы Стокса получаем

. (7.18)

Из выражения (7.18) находим

, (7.19)

где - плотность тока.

Формула (7.19) представляет математическое выражение теоремы о циркуляции в дифференциальной форме.

Надо отметить, что полученные соотношения (7.16) и (7.19) справедливы только для стационарных процессов (для постоянного тока).

Для нестационарных процессов, когда токи зависимы от времени, эти формулы неверны. Для доказательства этого утверждения выполним операцию дивергенции от обеих частей равенства (7.19):

или

.

Так как с математической точки зрения , то , что выполняется только в случае постоянного тока, т.к. из уравнения непрерывности для тока только для постоянного тока, когда

.

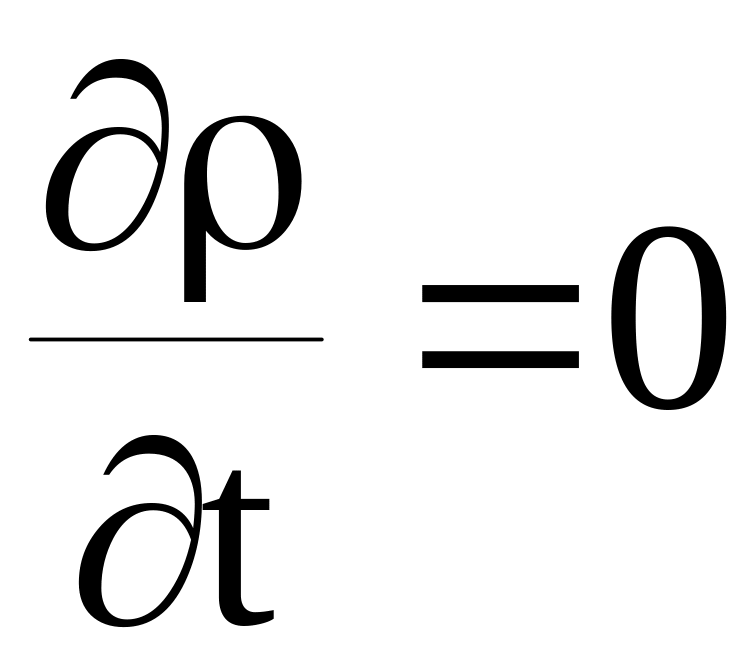Если же ток переменный, то объемная плотность заряда в отдельных точках цепи является переменной величиной, следовательно,

.

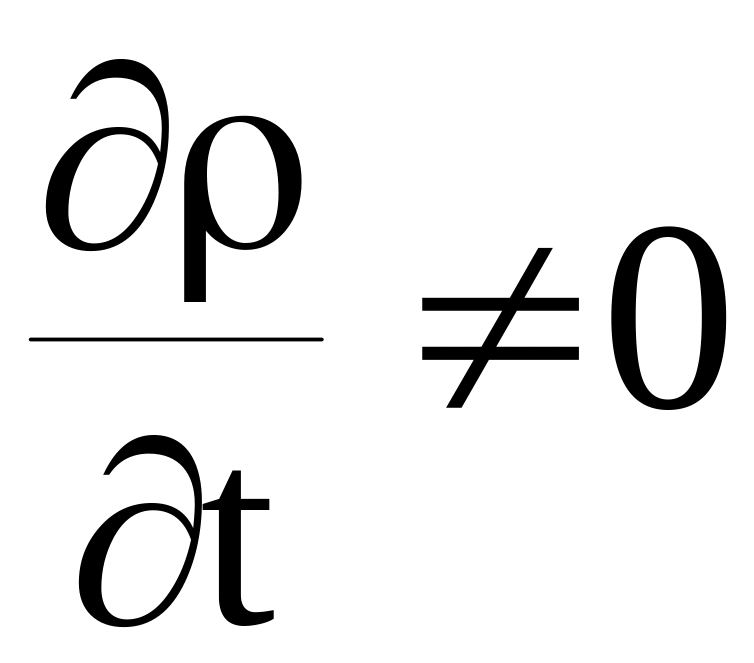7.4. Ток смещения

Смысл уравнения основного закона электромагнитной индукции

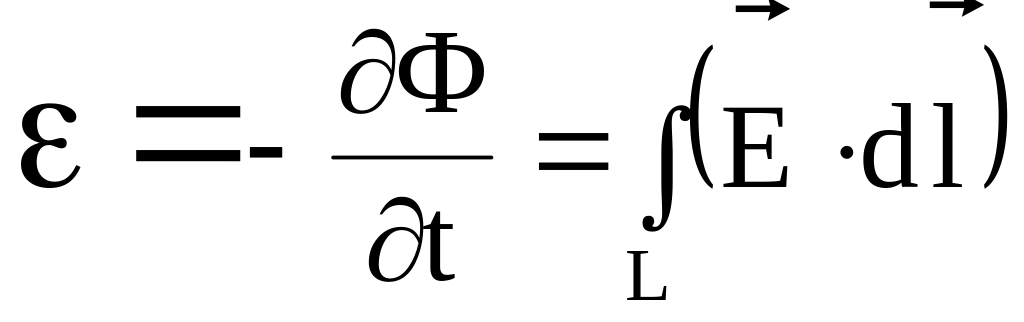
заключается в том, что изменяющееся магнитное поле создает вихревое электрическое поле, последнее в свою очередь вызывает в окружающем пространстве (веществе или вакууме) изменяющееся магнитное поле. Поскольку магнитное поле создается электрическим током, то вихревое электрическое поле следует рассматривать как некоторый ток, который протекает как в веществе, так и в вакууме. Максвелл назвал этот ток током смещения.

Таким образом, ток смещения – это изменяющееся со временем электрическое поле (вихревое электрическое поле), которое порождает магнитное поле так же, как и ток проводимости.

М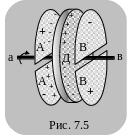 еханизм тока смещения можно установить, рассмотрев один из опытов А.А. Эйхенвальда. В этом опыте (рис. 7.5) диэлектрический диск Д вращается между четырьмя неподвижными заряженными полудисками А, А₁, В, В₁. При прохождении точками диска Д плоскости «ав», перпендикулярной чертежу и разделяющей заряженные полудиски, меняется направление электрического поля (знак поля), действующего на диэлектрик. В результате чего происходит изменение знака поляризационных зарядов диэлектрика. Если вращение диска происходит, так как показано на рис. 7.5, то на левой стороне диска вместо положительных зарядов при переходе через плоскость «ав» появляются отрицательные заряды, а на правой стороне вместо отрицательных зарядов появляются положительные заряды. Это означает, что в движущемся диске в плоскости «ав» происходит как бы движение зарядов: слева направо положительных, а справа налево отрицательных. Эти движения зарядов, представляющие собой смещение зарядов в молекулах диэлектрика, образуют ток смещения в диэлектрике, текущий слева направо. Эйхенвальд установил, что токи смещения (как и конвекционные токи) создают магнитное поле.

Т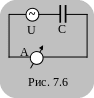 оки смещения наблюдаются в конденсаторах, включенных в цепь переменного тока (рис. 7.6). Известно, что для постоянного тока конденсатор, включенный в цепь последовательно, является бесконечно большим сопротивлением, если его диэлектрик не обладает утечкой. В такой цепи лишь в момент ее замыкания протекает импульс зарядного тока, соответствующий небольшому смещению электронов проводимости. Если в цепи с конденсатором существует источник переменного тока, то в такой цепи за каждый период протекают токи заряда и разряда конденсатора. Сопротивление конденсатора при этом не бесконечно велико, а зависит от емкости конденсатора и частоты тока:

.

В этом случае конденсатор необходимо рассматривать не как разрыв цепи, а как участок цепи с другим механизмом проводимости. Если между обкладками конденсатора находится полярный или поляризующийся в электрическом поле диэлектрик, то при приложении разности потенциалов к обкладкам конденсатора электрические заряды смещаются вдоль линий напряженности электрического поля. Это смещение зарядов (ионов) образует ток смещения в диэлектрике. Ток смещения существует не только в диэлектрике, но и в вакууме, где он представляет собой изменение напряженности электрического поля во времени.

Рассмотрим процессы, протекающие в схеме, представленной на рис. 7.6, где источник переменного тока (генератор), напряжение которого U, заряжает и перезаряжает конденсатор емкостью С. Если конденсатор плоский, то его емкость , заряд конденсатора . Тогда зарядный ток, который является током смещения, протекающий через конденсатор,

.

Плотность этого тока

.

В векторной форме

, (7.20)

где D – вектор индукции электрического поля.

Так как , где - вектор поляризации, то плотность тока смещения в диэлектриках

, (7.21)

где - плотность тока смещения в вакууме;

- плотность тока поляризации (тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике), который представляет собой смещение зарядов в неполярных молекулах, поворот диполей в полярных молекулах.

Полный ток в проводящей цепи равен сумме тока проводимости (а также конвекционного тока) и тока смещения.

Поэтому плотность полного тока равна

, (7.22)

где j – вектор плотности тока проводимости.

Так как ток смещения определяется производной , а не самой величиной вектора индукции электрического поля, то при убывании поля (например, внутри конденсатора, обладающего проводимостью при его разрядке) производная отрицательна. Ток смещения направлен от минуса к плюсу, в то время как ток проводимости всегда направлен от плюса к минусу, поэтому полный ток будет равен

.

При равенстве токов смещения и проводимости полный ток может быть равен нулю.

С учетом того что для полного тока , имеем

, (7.23)

где - проекция вектора плотности тока проводимости на направление положительной нормали к выбранной поверхности S;

- проекция вектора плотности индукции вихревого электрического поля на направление положительной нормали к выбранной поверхности S.

Уравнение (7.23) представляет собой обобщение закона полного тока на случай любых токов и выражает одно из основных положений теории Максвелла: токи смещения (а также конвекционные токи) создают такие же магнитные поля, как и токи проводимости.