
- •Задача 8.6
- •Задача 9.12
- •Задача 10.26
- •Задача 11.3
- •Используемая литература
- •Задача 8.6
- •Построить ряд распределения и столбцовую диаграмму;
- •Найти функцию распределения и построить ее график;
- •Вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение.
- •Задача 8.6
- •Построить ряд распределения и столбцовую диаграмму;
- •Найти функцию распределения и построить ее график;
- •Вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение.
Задача 11.3
Считается,
что изделие –
высшего качества, если отклонение его
размеров от номинальных не превосходит
по абсолютной величине
![]() -
4мм.
Случайные отклонения размера изделия
от номинального подчиняются нормальному
закону со средним квадратичным
отклонением, равным
-
4мм.
Случайные отклонения размера изделия
от номинального подчиняются нормальному
закону со средним квадратичным
отклонением, равным
![]() -
5 мм.
Систематические
отклонения отсутствуют. Определить
среднее число изделий высшего качества
среди 100 изготовленных.
-
5 мм.
Систематические
отклонения отсутствуют. Определить
среднее число изделий высшего качества
среди 100 изготовленных.
Решение:
Используем формулу расчета вероятности отклонения нормально распределенной случайной величины Х от своего математического ожидания:
![]() ,
где
,
где
![]() – величина отклонения случайной величины
Х от ее математического ожидания.
– величина отклонения случайной величины
Х от ее математического ожидания.
По
условию
= 200, M [X] = m = 2000 у. е.,
![]() у.
е.
у.
е.
![]()
в) Определим вероятность того, что число заказов за месяц отклонится от математического ожидания больше чем на 200 у. е., то есть
![]() .
.
Это вероятность события, противоположного по отношения к событию, – стоимость заказов за месяц отклонится от математического ожидания меньше чем на 200 у. е., следовательно,
![]() .
.
На рисунке 9 штриховкой выделена фигура, площадь которой равна вероятности того, что стоимость заказов за месяц отклонится от математического ожидания более чем на 200 у. е.
Используемая литература
1 Азизов А.М., Курицын А.Г., Никитенко В.Г. Основы прикладной математики. Теория вероятностей и математическая статистика. Спб: Химия, 1994.264 с.
2 Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высш. школа, 1998. 478 с.
3 Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. школа, 1998. 399 с.
4 Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения. М.: Наука, 1988. 480 с.
5 Мацкевич И. П., Свирид Г. П. Высшая математика: теория вероятностей и математическая статистика. Минск: Вышэйшая школа, 1993. 268 с.
6 Сазонова Е.Л. , Теория вероятностей и математическая статистика. Ч. 1. Теория вероятностей: Пособие для студентов факультета безотрывного обучения/ Под ред. В. С. Серёгиной. – Гомель: БелГУТ, 2000. – 95 с.
7 Смирнов Н. В., Дунин-Барковский И. В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1969. 511 с.
Задача 8.6
Для определения в условии дискретной случайной величины:
Построить ряд распределения и столбцовую диаграмму;
Найти функцию распределения и построить ее график;
Вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение.
Имея в запасе 3 патрона, стрелок производит выстрелы в мишень до первого попадания, или, пока не израсходует все патроны. Вероятность попадания при каждом выстреле равна 0,8. Случайная величина X – число выстрелов, произведенных в мишень.
1)
Законом распределения дискретной
случайной величины называется соответствие
между значениями
![]() этой величины и их вероятностями
этой величины и их вероятностями
![]()
Воспользуемся формулой Бернулли:
![]() ,
где 0 p
3 ;
q
= 1 – p;
m
= 0, 1, 2,…, n.
,
где 0 p
3 ;
q
= 1 – p;
m
= 0, 1, 2,…, n.
![]() ·
0,80·0,23
=
0,008
·
0,80·0,23
=
0,008
![]() 0,81·0,22
=
0,096
0,81·0,22
=
0,096
![]() 0,82·0,21
=
0,384
0,82·0,21
=
0,384
![]() 0,83·0,20
=
0,512
0,83·0,20
=
0,512
Простейшим способом задания закона распределения дискретной случайной величины является ряд распределения.
xi |
0 |
1 |
2 |
3 |
Итого |
pi |
0,008 |
0,096 |
0,384 |
0,512 |
1 |
xi· pi |
0 |
0,096 |
0,768 |
1,536 |
2,4 |
xi2· pi |
0 |
0,096 |
1,536 |
4,608 |
6,24 |
Построим столбцовую диаграмму
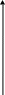
pi |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,512 |
|
|
|
|
0,384 |
|
|
|
|
|
|
|
|
|
0,096 |
|
|
|
|
0,008 |
|
|
|
|
0 |
1 |
2 |
3 |
xi |
Рисунок 1 - Столбцовая диаграмма
Вычислим функцию распределения данной случайной величины:
:
при x , 0] ;
при
x 0, 1]
![]() ;
;
при
x 1, 2]
![]() ;
;
при
x 2, 3]
![]() ;
;
приx 3, +)
![]()
![]()
Итак, функция распределения рассматриваемой случайной величины имеет вид:
![]()
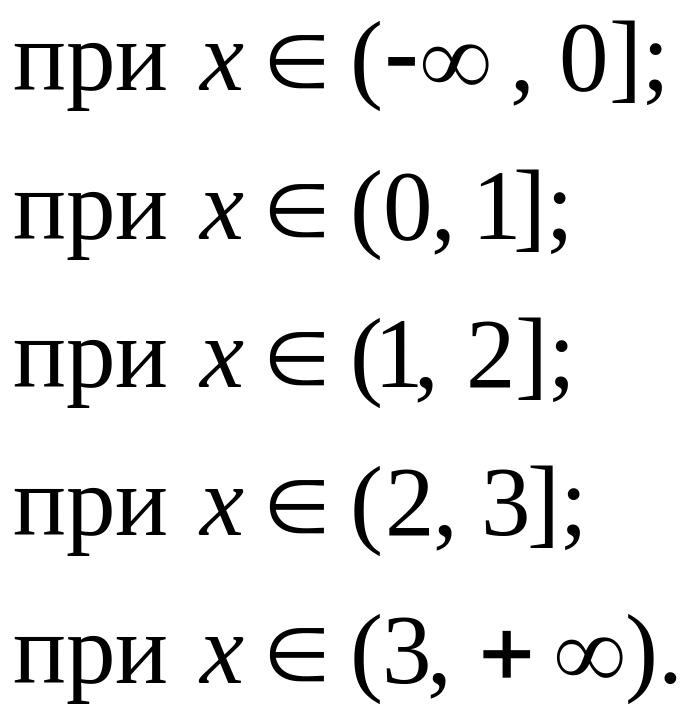
График функции F(x) приведён на рисунке 2.
F(x) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,488 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,104 |
|
|
|
|
0 |
|
|
|
|
0 |
1 |
2 |
3 |
xi |
Рисунок 2 – Функция распределения
3) Вычислим числовые характеристики данной случайной величины.
Математическое ожидание
![]() [попаданий],
[попаданий],
т. е. среднее число попаданий, которые стрелок сможет сделать, равно 2,4. Как следует из ряда распределения, данная случайная величина имеет моду: , т. е. наиболее вероятное число попаданий, которое стрелок сможет сделать, равно 3.
Дисперсия
![]() [попаданий2].
[попаданий2].
Среднее
квадратическое отклонение
![]() [попаданий].
[попаданий].


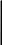





 ,008
,008