МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «прикладная математика»

контрольная работа №2

по дисциплине

«основы теории вероятностей»

Выполнил студент факультета ФБО Группы 09-ЗБ-21 Шифр 278 Киселева Л.А.

Гомель 2011г.

Содержание

контрольная работа №2

Задача 8.6 3

Задача 9.12 5

Задача 10.26 8

Задача 11.3 9

Используемая литература 10

Задача 8.6 11

Задача 8.6 13

Задача 8.6

Для определения в условии дискретной случайной величины:

1. Построить ряд распределения и столбцовую диаграмму;

2. Найти функцию распределения и построить ее график;

3. Вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение.

Имея в запасе 3 патрона, стрелок производит выстрелы в мишень до первого попадания, или, пока не израсходует все патроны. Вероятность попадания при каждом выстреле равна 0,8. Случайная величина X – число выстрелов, произведенных в мишень.

Х может принимать значения 1,2,3.

p = 0,8

q = 1- p = 1-0,8=0,2

P (x=1) = p = 0,8 при первом же выстреле произошло попадание;

P (x=2) = qp = 0,2·0,8 = 0,16 при первом выстреле промах, при втором выстреле произошло попадание;

P (x=3) = q²p = 0,2²·0,8+0,2³ = 0,04 при двух выстрелах промах, при третьем выстреле произошло попадание, либо при трех выстрелах промах;

Простейшим способом задания закона распределения дискретной случайной величины является ряд распределения.

xi	1	2	3	Итого
pi	0,8	0,16	0,04	1
xi· pi	0,8	0,32	0,12	1,24
xi2· pi	0,8	0,64	0,36	1,80

Построим столбцовую диаграмму

0,04

08

0,16

0,8

P_i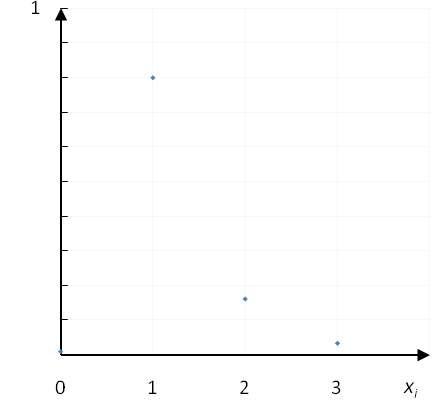

Рисунок 1 - Столбцовая диаграмма

Вычислим функцию распределения данной случайной величины:

:

при x   , 1] ;

при x  1;2] ;

при x  2; 3] ;

при x  3; +) ;

Итак, функция распределения рассматриваемой случайной величины имеет вид:

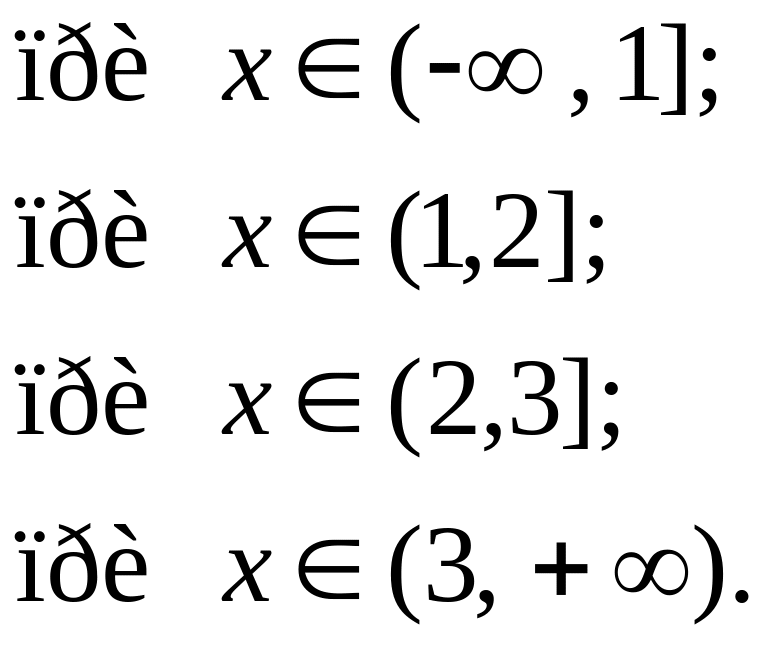
График функции F(x) приведён на рисунке 2.

F 1 0,96 0,8 (x)
0	1	2	3	xi

Рисунок 2 – Функция распределения

3) Вычислим числовые характеристики данной случайной величины.

Математическое ожидание

[попаданий],

т. е. среднее число попаданий, которые стрелок сможет сделать, равно 1,24. Как следует из ряда распределения, данная случайная величина имеет моду: , т. е. наиболее вероятное число попаданий, которое стрелок сможет сделать, равно 3.

Дисперсия

[попаданий²].

Среднее квадратическое отклонение [попаданий].