Пример 4

В сеть трехфазного тока с линейным напряжением U_Л = 380 В подключена нагрузка по схеме «звезда» (рисунок 7). Сопротивления фаз: R₁ = Ом, X_C1 = 8 Ом,

X_C2 = 20 Ом, R₃ = 3 Ом, X_L3 = 4 Ом. Определить:

1. линейные токи;

2. ток в нейтральном проводе с помощью векторной диаграммы;

3. активную, реактивную и полную мощности, потребляемые цепью.

R1 X_C1

A

U_Л

X_C2

B

R₃ X_L3

C

N

Рисунок 7

Решение:

1. Определить фазное напряжение:

В трехфазной четырехпроводной «звезде» линейное напряжение больше фазного

в √ 3 раз, т.е. фазное напряжение U_Ф = U_Л / √ 3 = 380 / √ 3 = 220 В.

2. Определить реактивные сопротивления фаз:

X_A = X_L1 - X_C1 = -X_C1 = - 8 Ом, т.к. индуктивное сопротивление в фазе А отсутствует;

X_B = X_L2 - X_C2 = -X_C2 = - 20 Ом, т.к. индуктивное сопротивление в фазе В отсутствует;

X_C = X_L3 - X_C3 = X_L3 = 4 Ом, т.к. емкостное сопротивление в фазе С отсутствует.

3. Определить полные сопротивления фаз:

Z_A = √ R₁² + X_C1² = √ 6² + 8² = √ 100 = 10 Ом;

Z_B = X_C2 = 20 Ом, т.к. фаза А содержит только емкостное сопротивление;

Z_C = √ R₃² + X_L3² = √ 3² + 4² = √ 25 = 5 Ом.

4. Определить фазные токи:

I_A = U_ф / Z_A = 220 / 10 = 22 A;

I_B = U_ф / Z_B = 220 / 20 = 11 A;

I_C = U_ф / Z_C = 220 / 5 = 44 A.

При соединении трехфазного потребителя по схеме «звезда» линейные токи равны фазным, т.е. найденные фазные токи являются также линейными токами.

5. Определить активную мощность цепи:

P = P_A + P_B + P_C,

где P_A = I_A² ∙ R₁ = 22² ∙ 6 = 2904 Вт – активная мощность фазы А,

P_B = 0 – активная мощность фазы В ( в фазе В нет активного сопротивления),

P_C = I_C² ∙ R₃ = 44² ∙ 3 = 5808 Вт – активная мощность фазы С;

P = 2904 + 0 + 5808 = 8712 Вт.

6. Определить реактивную мощность цепи:

Q = Q_A + Q_B + Q_C,

где Q_A = I_A² ∙ X_A = 22² ∙ (- 8) = - 3872 ВАр – реактивная мощность фазы А,

Q_B = I_B² ∙ X_B = 11² ∙ (-20) = - 2420 ВАр – реактивная мощность фазы B,

Q_C = I_C² ∙ X_C = 44² ∙ 4 = 7744 ВАр – реактивная мощность фазы C;

Q = - 3872 – 2420 + 7744 = 1452 ВАр.

7. Определить полную мощность цепи:

S = √ P² + Q² = √ 8712² + 1452² = 8832 ВА.

8. Определить углы сдвига фаз между напряжением и током в каждой фазе:

sin φ_А = X_A / Z_A = - 8 / 10 = - 0,8

φ_А = arcsin (- 0,8) = 53⁰;

sin φ_B = X_B / Z_B = - 20 / 20 = - 1

φ_B = arcsin (- 1) = - 90⁰;

sin φ_С = X_С / Z_С = 4 / 5 = 0,8

φ_С = arcsin 0,8 = 53⁰.

9. Построить векторную диаграмму:

• выбрать масштаб: по напряжению m_U = 40 В/см;

по току m_I = 11 В/см;

• определить длины векторов:

фазных напряжений – l_UФ = U_Ф / m_U = 220 / 40 = 5,5 см;

фазных токов – l_IA = I_A / m_I = 22 / 11 = 2 см;

l_IB = I_B / m_I = 11 / 11 = 1 см;

l_IC = I_C / m_I = 44 / 11 = 4 см;

• построить в выбранном масштабе вектора фазных напряжений Ū _A, Ū _B, Ū _C под углом 120⁰ относительно друг друга;

• под углами φ_А, φ_B, φ_С к соответствующим векторам фазных напряжений отложить вектора фазных токов Ī_A, Ī_B, Ī_C:

ток в фазе А опережает фазное напряжение (φ_А = - 53⁰),

ток в фазе В опережает фазное напряжение (φ_В = - 90⁰),

ток в фазе С отстает от фазного напряжения (φ_С = 53⁰);

• геометрическая сумма фазных токов равна току в нулевом проводе:

Ī_N = Ī_A + Ī_B + Ī_C;

• значение тока в нулевом проводе определить по формуле:

I_N = l_IN ∙ m_I ,

где l_IN – длина вектора тока в нулевом проводе, см

I_N = 6 ∙ 11 = 66А.

Результаты построения векторной диаграммы представлены на рисунке 8

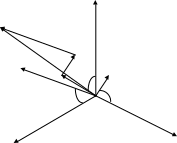
U_A

I_C

I_N

I_B

I_A φ_A I_B

I_C

φ_C φ_B

U_C U_B

Рисунок 8

Ответ: I_A = 22 A; I_B = 11 A; I_C = 44 A; I_N = 66 A;

P = 8712 Вт; Q = 1452 Вар; S = 8832 ВА.