
- •Математика
- •Основные понятия теории числовых рядов.
- •Свойства положительных числовых рядов. Необходимый признак сходимости.
- •Сходимость положительных числовых рядов :признаки сравнения.
- •Сходимость положительных числовых рядов : радикальный признак Коши, признак д’аламбера, интегральный признак Коши.
- •Сходимость знакопеременных и знакочередующихся числовых рядов. Признак лейбница. Абсолютная и условная сходимость.
- •Функциональные ряды. Основные понятия.
- •Степенные ряды. Теорема Абеля.
- •Определение радиуса и области сходимости степенных рядов.
- •Ряды тейлора и Маклорена. Разложение функизй на ряды Тейлора и Маклорена.
- •Случайное событие и основные понятия свзязаные с ним.
- •Определение вероятности: аксиоматическое классическое статическое геометрическое.
- •Свойства вероятности.
- •Теоремы сложения и умножения вероятностей для совместных и не совместных событий.
- •Формула полной вероятности и формула байесса
- •Основные понятия и формулы комбинаторики.
- •Повторные испытания. Формула бернулли.
- •Дискретная случайная величина и ее закон распределения.
- •Числовые характеристики дискретных случайных величин
Математика
(29-56)
Основные понятия теории числовых рядов.
Числовой ряд – это сумма членов числовой последовательности вида:
![]()
ak - называют общим членом числового ряда или k–ым членом ряда.
В качестве примера числового
ряда можно привести сумму бесконечно
убывающей геометрической прогрессии
со знаменателем q
= -0.5: 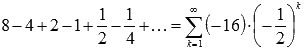 .
.
Числовой ряд ![]() называется сходящимся,
если существует конечный предел
последовательности частичных сумм
называется сходящимся,
если существует конечный предел
последовательности частичных сумм ![]() .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется
расходящимся.
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется
расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть, ![]() .
.
Еще одним
примером расходящегося числового ряда
является сумма вида ![]() .
.
В этом
случае n–ая частичная
сумма может быть вычислена как ![]() .
Предел частичных сумм бесконечен
.
Предел частичных сумм бесконечен ![]() .
.
Сумма
вида ![]() называется гармоническим
числовым рядом.
называется гармоническим
числовым рядом.
Свойства положительных числовых рядов. Необходимый признак сходимости.
Теорема. Если ряд сходится, то предел его общего члена при
![]()
равен нулю, т.е.
![]()
Следствие. Если предел общего члена ряда при
не равен нулю, то ряд расходится.
Пусть
дан ряд ![]() все
слагаемые которого положительны
все
слагаемые которого положительны ![]() .
.
Признак
Коши. Пусть
существует ![]() .
Тогда
.
Тогда
если ![]() ,
то ряд
сходится;
,
то ряд
сходится;
если ![]() ,
то ряд
расходится;
,
то ряд
расходится;
если ![]() ,
то о сходимости или расходимости ряда
ничего сказать нельзя.
,
то о сходимости или расходимости ряда
ничего сказать нельзя.
Признак
Даламбера. Пусть
существует  .
Тогда
.
Тогда
если ![]() ,
то ряд
сходится;
,
то ряд
сходится;
если ![]() ,
то ряд
расходится;
,
то ряд
расходится;
если ![]() ,
то о сходимости или расходимости ряда
ничего сказать нельзя.
,
то о сходимости или расходимости ряда
ничего сказать нельзя.
Сходимость положительных числовых рядов :признаки сравнения.
Признак сравнения:
Теорема (признак сравнения). Пусть даны два ряда с положительными членами
![]()
причём члены первого ряда не превосходят соответствующих членов второго, т.е.
![]()
Тогда из сходимости второго ряда следует сходимость первого, а из расходимости первого ряда – расходимость второго.
Сходимость положительных числовых рядов : радикальный признак Коши, признак д’аламбера, интегральный признак Коши.
Интегральный признак Коши:
Пусть f(x)
– некоторая функция, определенная на
интервале [1, ¥). В этом разделе
рассматриваются ряды вида  ,
то есть ряды со слагаемыми вида
,
то есть ряды со слагаемыми вида ![]() .
.
Интегральный
признак Коши. Пусть
при x®¥ функция f(x) монотонно убывает
до нуля, то есть ![]() .
Тогда ряд
.
Тогда ряд  сходится
или расходится одновременно с интегралом
сходится
или расходится одновременно с интегралом 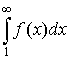 .
.
Признак Д’аламбера:
Признак Даламбера. Пусть существует . Тогда
если , то ряд сходится;
если , то ряд расходится;
если , то о сходимости или расходимости ряда ничего сказать нельзя.
Радикальный признак Коши:
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
![]()
с неотрицательными членами
существует такое число ![]() ,
, ![]() ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство ![]() ,
то данный ряд сходится.
,
то данный ряд сходится.
Сходимость знакопеременных и знакочередующихся числовых рядов. Признак лейбница. Абсолютная и условная сходимость.
Числовой ряд называется знакоположительным, если un>0 при всех n=1,2,3… .
Если первый член знакочередующегося ряда положителен, то этот ряд можно записать в виде
![]()
а если отрицателен – виде
![]()
Признак
Лейбница. Если
при ![]() ,
то ряд
,
то ряд  сходится.
сходится.
Для
этого случая имеет место следующая
оценка остатка ряда ,то
есть остаток ряда меньше первого
отброшенного слагаемого.
,то
есть остаток ряда меньше первого
отброшенного слагаемого.
Абсолютная сходимость.
Для
знакопеременного ряда существует
понятие абсолютной и условной
сходимости.
Знакопеременный
ряд ![]() называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд
называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд ![]() .
.
Условная сходимость.
Знакопеременный ряд называется условно сходящимся, если ряд расходится, а ряд сходится.
