ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Контрольная работа

по дисциплине: Экономико-математические методы и

прикладные модели.

на тему: Оптимизационные экономико-математические модели.

Методы получения оптимальных решений.

Выполнил: Фролов Д.И.

группа: ФБ-МН104

Специальность: Бакалавр менеджмента

№ зач. книжки 11МЛД46048

Проверил: Бесхлебнова Г.А.

Москва-2012 Задача 1

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решить задачу на максимум, и почему?

Условие задачи:

Имеется два вида корма I и II, содержащие питательные вещества (витамины) , и . Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице.

Питательное вещество (витамин)	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
		I	II
	9	3	1
	8	1	2
	12	1	6

Стоимость 1 кг корма I и II соответственно равна 4 и 6 ед.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание питательных веществ каждого вида было бы не менее установленного предела.

Решение:

Составим уравнения прямой оптимизационной задачи на минимум затрат. Корм первого и второго видов обозначим как и соответственно.

Ограничения:

– ограничение по содержанию питательного вещества S₁

– ограничение по содержанию питательного вещества S₂

– ограничение по содержанию питательного вещества S₃

,

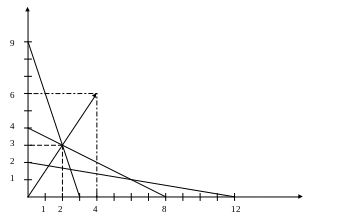
Решим полученную задачу линейного программирования графическим методом. Построим прямые ограничений:

I 3х₁ + х₂ = 9, проходящей через точки (3;0) и (0;9)

II х₁ + 2х₂ = 8, проходящей через точки (8;0) и (0;4)

III х₁ + 6х₂ = 12, проходящей через точки (12;0) и (0;2)

и линию уровня:

Для нахождения экстремального значения целевой функции построим вектор – градиент, координаты которого являются частными производными функции , т.е. (4;6). Для построения вектора соединим данную точку с началом координат. Т.к. задача решается на минимизацию функции, поэтому линию уровня, которая формируется перпендикулярно вектору – градиенту, будем перемещать в направлении, противоположенном направлению вектора. Линию перемещаем до ее пересечения с крайней точкой входящей в область допустимых значений, в данной задаче этой точкой является точка с координатами (2;3).

Проверка:

3 Х₁+Х₂ = 9

1Х₁+2Х₂= 8

Х₁ = 8 - 2Х₂

3*(8 - 2Х₂) +Х₂ = 9

24- 6Х₂ +Х₂ = 9

Х₂ = 3; Х₁= 8-2Х₂=8-2*3=2 (верно).

ЦФ (2;3) = 4*2+6*3= 26.

Ответ: чтобы обеспечить максимальную полезность корма с минимальными затратами следует взять 2 единицы корма I вида и 3 единицы корма II вида. С таким дневным рационом связаны затраты в 26 ден. ед.

Задача на максимум не разрешима, т.к. не существует конечного максимума на неограниченном множестве допустимых решений (вследствие неограниченности целевой функции на ОДР).