16.Установившееся и неустановившееся, равномерное и неравномерное, напорное и безнапорное движение жидкости.
Движение жидкости определяется скоростью
в отдельных точках, давлениями,
возникающими на различных глубинах,
глубинами, а также общей формой потока.
Указанные величины являются функциями
координат
а также могут изменятся во времени
,
в связи с чем различают:
- установившееся движение жидкости (рис. 23а), при котором скорости, давления, глубины не меняются с течением времени, а зависят только от положения в потоке жидкости рассматриваемой точки, являясь функцией координат
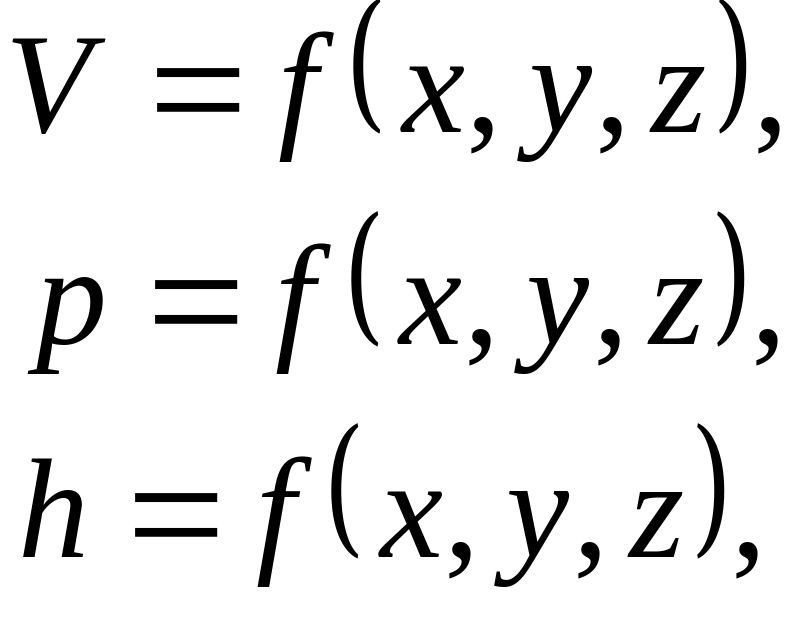
где - скорость движения;
-
гидродинамическое давление;
-
глубина потока.
- неустановившееся движение жидкости (рис. 23б), при котором все перечисленные выше компоненты являются функцией не только координат, но и времени (т.е. изменяются с течением времени)
а) б)
баки
при постоянном уровне
при переменном уровне
насосы
центробежный
поршневой
Рисунок 23 - Примеры установившегося и неустановившегося движения
Установившееся в свою очередь
подразделяется на равномерное и
неравномерное. Равномерным называется
такое установившееся движение, при
котором живые сечения вдоль всего потока
не изменяются, в этом случае
и
(рис 24).
Н
еравномерным
называется такое движение, при котором
распределение скоростей неодинаково
в различных поперечных сечениях; при
этом средняя скорость и площадь сечения
могут быть и постоянными.
Рисунок 24 – Примеры равномерного,
неравномерного, напорного и безнапорного
движения.
Напорным называется такое
движение жидкости, при котором
поток полностью заключен в твердые
стенки и не имеет свободной поверхности.
Движение происходит за счет разности
давлений
и под действием силы тяжести.
Безнапорным называется поток, имеющий свободную поверхность. Движение - за счет силы тяжести и начальной скорости.
Еще один вид движения жидкости - свободная струя, не ограниченная твердыми стенками. В этом случае движение жидкости происходит по инерции и под действием силы тяжести.
17.Два режима движения жидкостей и газов. Опыты Рейнольдса, критерий Рейнольдса.
При исследованиях вопроса о механизме самого движения жидкостей пришли к заключению о существовании двух различных, резко отличающихся режимов движения. Это было известно еще в первой половине XIX века, физиком Рейнольдсом на основе весьма простых и наглядных опытов.
Рисунок 31 – Схема установки Рейнольдса
Рейнольдс пропускал жидкость из бака Б, в котором с помощью перелива 7 поддерживался постоянный уровень, через стеклянные трубки различного диаметра, регулируя скорость движения жидкости в них кранами 1 и 5. По тонкой трубке 3 с заостренным концом ко входу в стеклянную трубку 4 подводилась окрашенная жидкость из сосуда 2. Средняя скорость V в трубке 4, имеющей площадь сечения со определялась по объему жидкости W, поступившей в мерный сосуд 6 за время t (рис .31).
Как показывают исследования, структура потока при различных скоростях течения различна.
При малых скоростях течения в потоке жидкости появляются окрашенные струйки. Они движутся прямолинейно, без пульсаций, не перемешиваясь с соседними слоями жидкости (рис. 31а). Такое параллельно-струйное, спокойное движение жидкости без поперечного перемешивания и при отсутствии пульсации скорости и давления называют ламинарным (слоистым) режимом движения жидкости.
При постепенном увеличении скорости движения жидкости при некоторой скорости течения параллельно-струйное движение нарушится, окрашенные струйки станут пульсирующими, появятся разрывы. А при дальнейшем увеличении скорости окрашенные струйки исчезнут, перемешавшись с потоком жидкости (рис. 316). Движение станет беспорядочным вследствие пульсации скоростей и давления, что и приводит к перемешиванию частиц жидкости. Движение жидкости, во время которого происходит пульсация скоростей и давления, называют турбулентным (беспорядочным) режимом движения.
Обобщив результаты своих опытов, Рейнольдс нашел общие условия, при которых возможны существование того или иного режима или переход одного режима к другому. Он установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости V, внутренний диаметр трубы d, плотность жидкости р, динамическая вязкость rj.
Для характеристики режима движения Рейнольде ввел безразмерный параметр Re, учитывающий влияние перечисленных факторов, называемый числом (или критерием) Рейнольдса.
но
,
тогда
.
Границы существования того или иного режима движения жидкости определяются двумя числами Рейнольдса, которые называются критическими: нижним ReKP.H.=2320 и верхним ReKp.B.=13800 (сам Рейнольдс получил несколько иные значения ReKP.H.=2000 Rckp.b.=12000). Значения скоростей, соответствующие этим значениям числа Рейнольдса, также называют критическими (нижней критической Vh.k. и верхней критической Vb.k.)-
Таким
образом, при Re
< Rckp.h
(
соответственно , V<
Vh.k)
возможен
только ламинарный
режим, при Re>
Reкр.н.B
(V>
Vв.к)
- турбулентный, а при
,или
.)
наблюдается
неустойчивое состояние потока.
Тогда, для определения характера режима движения жидкости необходимо в каждом отдельном случае вычислять число Рейнольдса Re=Vd/v и сравнивать результат с критическими значениями.
В настоящее время при расчетах принято исходить только из нижнего значения критического числа Рейнольдса Reкp.=2320 и считать режим ламинарным при Re < 2320, а турбулентным при Re> 2320. При этом движение в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности в гидравлических расчетах.
С физической точки зрения критерий Re есть отношение сил инерции потока к силам трения при его движении.
Определение режима движения жидкости в практических расчетах имеет очень важное значение. Опыты показали, что потери напора по длине потока при ламинарном режиме движения пропорциональны средней скорости в первой степени:
,
где:
-
потери напора по длине потока;
кл -коэффициент пропорциональности;
V - средняя скорость течения потока
Для турбулентного режима движения потери напора по длине потока пропорциональны средней скорости в степени n:
где: n – показатель степени, изменяющийся от 1,75 до 2 .
Покажем на графике (рис. 32) соотношение между потерями напора и числом Re. Как видно, с увеличением числа Рейнольдса показатель степени увеличивается. При развитой турбулентности n=2. Следовательно, при определении потерь напора надо знать характер режима движения, а затем уже выбрать соответствующую формулу для определения потерь напора.
Рисунок
32 - Зависимость
