14.Основные понятия гидродинамики: линии и трубки тока, траектория частицы, поток жидкости, живое сечение потока, смоченный периметр, гидравлический радиус, гидравлический диаметр, расход.

П ри рассмотрении движения жидкости пользуются следующими понятиями и определениями:

Л инией тока (рис. 25)называется кривая, проведенная в жидкости, касательные к которой в каждой точке совпадают с направлением векторов скоростей частиц, лежащих в данный момент на этой кривой, причем каждая последующая частица расположена на направлении вектора скорости предыдущей.

Рисунок 25 – Линия тока и траектория, трубка тока.

Т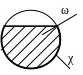 раекторией частицы называется путь, описанный частицей в пространстве.

В ыберем в жидкости замкнутый контур и проведем через каждую его точку линию тока и получим трубку тока.

Т

Рисунок 26 – Живое сечение потока, гидравлический радиус и диаметр,

смоченный периметр

рубкой тока называется трубчатая поверхность, образованная линиями тока, проходящими через все точки конечно малого замкнутого контура, причем все его

точки принадлежат различным линиям тока. Жидкость, движущаяся внутри трубки тока, называется элементарной струйкой (элементарная струйка абсолютно непроницаемая).

Потоком жидкости называется совокупность элементарных трубок, текущих в заданных границах.

Живым сечением называется поверхность , проведенная в границах потока и нормальная ко всем линиям тока (рис.26).

Смоченным периметром называется часть периметра живого сечения, соприкасающегося с ограждающими стенками.

Гидравлический диаметр представляет собой отношение учетверенной площади живого сечения к смоченному периметру

.

Гидравлический радиус - это отношение площади живого сечения к смоченному периметру, он равен и соответственно .

Количество жидкости, проходящее через живое сечение в единицу времени, называется расходом. Расход может быть объемным, массовым, весовым.

Объемный: ,

Массовый: ,

Весовой: ,

где: - средняя скорость,

- площадь живого сечения,

- плотность,

-удельный вес.

Т.к. скорости различных струек реального потока в общем случае различны, то объемный расход всего потока равен:

.

Фиктивная скорость, с которой должны двигаться все частицы жидкости для обеспечения расхода называется средней скоростью.

,

откуда

тогда телом расхода, построенным на средней скорости, будет цилиндр с высотой и основанием, равным площади сечения потока .

15. Уравнение постоянства расхода (уравнение неразрывности)

О

Рисунок 27 – К уравнению неразрывности.

сновываясь на законе сохранения вещества, на предположении о сплошности течения и на свойстве трубки тока (ее непроницаемости) можно утверждать, что расход во всех сечениях элементарных струек один и тот же (рис. 27).

Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое формулируется так: элементарный расход жидкости при установившемся движении есть величина постоянная для всей элементарной струйки.

Аналогичное уравнение составим и для потока конечных размеров, введя среднюю скорость.

.

Уравнение неразрывности для потока жидкости читается так: расход жидкости через любое сечение потока при установившемся движении есть величина постоянная. Из уравнения неразрывности потока для двух сечений можно написать:

.

Из этого уравнения следует, что средняя скорость обратно пропорциональна площади сечения.