Оптическая разность хода лучей, отклоняющихся от первоначального направления под углом дифракции j, равна

D = d^.sinj,

где d – постоянная решетки (период). Период связан числом штрихов на единицу длины решетки соотношением:

d = 1/N₀ = l /N.

Максимум интенсивности дифракционного спектра наблюдается в том случае, когда в области фонта падающей на препятствие волны размер препятствия кратен нечетному числу длин полуволн, т.е. в области препятствия укладывается нечетное число зон Френеля. Однако в случае дифракционной решетки таких препятствия (щелей) много, и действие одной щели усиливается. Поэтому условие главных максимумов дифракционной решетки имеет вид:

,

где m = 0, 1, 2,….

Приравнивая выражения для оптической разности хода лучей, получим

d^.sinj = m^.l,

(l /N) ^.sinj = m^.l. (1)

Наибольшее число главных максимумов наблюдается при sinj = 1:

m_max = l/(Nl).

Сделаем вычисления:

m_max =10 ^-3/(400 ^.5,8 ^.10^-7)=4,3 » 4 .

Угол отклонения 4-го максимума от нормали определи из уравнения

sinj_max = m_max ^.l ^.N / l ,

sinj_max = 4 ^.5,8 ^.10 ^–7. 400 /10 ^–3 = 0,928,

j_max » 68,1⁰ .

Ответ: m_max = 4; j_max = 68,1⁰ .

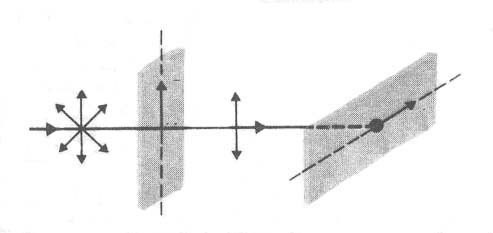
4. Интенсивность естественного света, прошедшего через поляризатор, уменьшилась в 2,3 раза. Во сколько раз она уменьшится, если за первым поставить второй такой же поляризатор так, что угол между их главным плоскостям (оптическим осями) равен 60⁰ ?

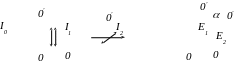Дано: Решение:

I₀ /I₁ = 2,3

a = 60⁰

I₀ /I₂ - ?

Естественный свет можно представить в виде суперпозиции двух некогерентных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность. Поляризатор пропускает колебания волны, параллельные его главной плоскости, и полностью задерживает колебания, перпендикулярные этой плоскости. Из первого поляризатора выходит плоскополяризованный свет интенсивностью

, (1)

где k – коэффициент, учитывающий отражение и поглощение света, I₀ – интенсивность естественного света.

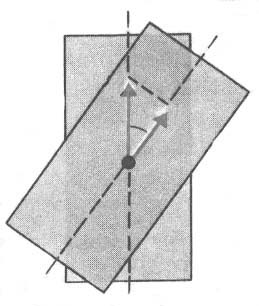
После прохождения второго поляризатора интенсивность уменьшается не только из-за отражения и поглощения света в нем, но и за счет несовпадения главных плоскостей (оптических осей) поляризаторов. По закону Малюса:

.

Следовательно,

, . (2)

Величину (1-k) найдем из (1), воспользовавшись данными в условии задачи:

.

Подставим это выражение в формулу (2) и получим расчетную формулу:

.

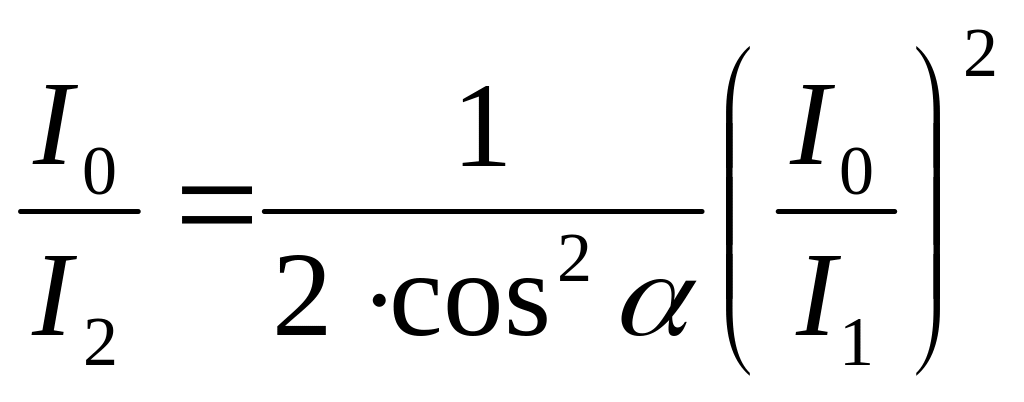Вычислим искомое отношение:

.

Ответ: I₀ /I₂ = 10,6.

5. Определить массовую концентрацию сахарного раствора в трубке, если при прохождении света через трубку длиной 20 см плоскость поляризации поворачивается на угол 10⁰. Удельное вращение сахара равно 1,17^.10 ^-2 рад^.м²/кг.

Дано: Решение:

l = 20 см = 0,20 м

j = 10⁰

[j₀] = 1,17^.10 ^-2 рад^.м²/кг

1⁰ = 1,75^.10 ^–2 рад

C - ?

Некоторые вещества, называемы оптически активными, способны поворачивать плоскость поляризации. Это вращение наблюдается, если между скрещенными поляризаторами (угол между их главными плоскостями 90⁰), дающими темное поле зрения, поместить такое вещество – поле зрения анализатора (второго из поляризаторов) просветляется. Тогда при повороте анализатора на некоторый угол j можно вновь получить темное поле зрения. Этот угол есть угол поворота плоскости поляризации света активным веществом. Для оптически активных растворов

j = [j₀]^.C^.l,

где l – расстояние, пройденное светом в веществе, [j₀] – удельное вращение, численно равное углу поворота плоскости поляризации при прохождении через вещество единичной толщины и концентрации. Следовательно, массовая концентрация сахарного раствора равна:

,

Ответ: C = 74,8 кг/м³.

6. Угол максимальной поляризации при отражении света от кристалла каменной соли равен 57⁰05'. Определить скорость распространения света в кристалле.

Дано: Решение:

a

a_Б

a_Б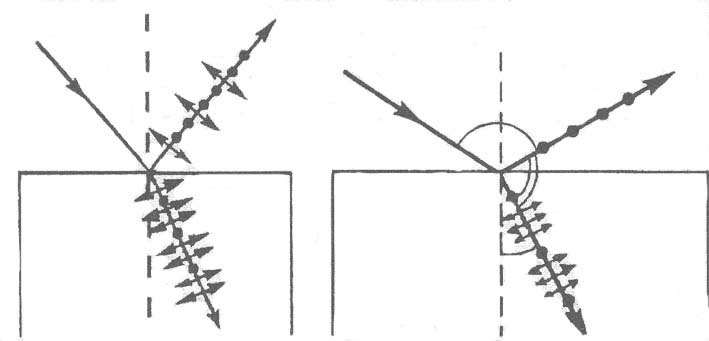

a_Б = 57⁰05'

с = 3^.10⁸ м/с

n₂

n₂

V_ф

V_ф - ?

Д. Брюстер обнаружил явление, когда при некотором угле падения a_Б естественного света на границу двух изотропных сред отраженный свет оказывается полностью плоскополяризованным. Угол Брюстера определяется выражением:

,

где n₂₁ = n₂ /n₁ – относительный показатель преломления второй среды относительно первой. Поскольку показатель преломления света в воздухе n₁ = 1, то

tga_Б =n₂ = с / V_ф.

Таким образом, фазовая скорость света в кристалле каменной соли равна

V_ф = с / tga_Б ;

V_ф = 3^.10⁸ / tg57⁰05'=3^.10⁸ /1,545 = 2^.10⁸ (м/с).

Ответ: V_ф= 2^.10⁸ м/с.