
- •Контрольные задания для студентов-заочников фм СмолГу
- •Тема 3 "Основы электричества и магнетизма" примеры решения задач по теме 3
- •Итак, напряженность равна
- •Индуктивность соленоида с однослойной обмоткой равна
- •Следовательно, эдс индукции можно выразить как
- •Приравнивая правые части этих выражений, получим
- •Задачи по теме 3 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 3 для рефератов (все каждому студенту)
- •Тема 4. Физика колебаний
- •Задачи по теме 4 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 4 для рефератов (все каждому студенту)
- •Тема 5. Волновые явления
- •Оптическая разность хода лучей, отклоняющихся от первоначального направления под углом дифракции j, равна
- •Приравнивая выражения для оптической разности хода лучей, получим
- •Угол отклонения 4-го максимума от нормали определи из уравнения
- •Задачи по теме 5 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 5 для рефератов (все каждому студенту)
- •Тема 6. Корпускулярно-волновые дуализм электромагнитного излучения
- •Мощность - это энергия, излучаемую за некоторый интервал времени:
- •Задачи по теме 6 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 6 для рефератов (все каждому студенту)
- •Тема 7. Элементы квантовой физики атомов, молекул и твердых тел
- •Задачи по теме 7 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 7 для рефератов (все каждому студенту) ?
- •Тема 8. Основы квантовой физики атомного ядра и элементарных частиц
- •Wсв МэВ/нукл Тогда дефект массы равен
- •Задачи по теме 8 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
- •Вопросы по теме 8 для рефератов (все каждому студенту)
- •Тема 3: "Основы электричества и магнетизма"
- •Диэлектрическая проницаемость (относительная)
- •Удельное сопротивление (r) и температурный коэффициент сопротивления (a) проводников
- •Эдс (e) и рабочее напряжение (u)
- •Электрические свойства металлов1
- •Свойства полупроводников2
- •Магнитные свойства магнитно-мягких материалов3
- •Магнитные свойства магнитно-твёрдых материалов4
- •Тема 5. Волновые явления
- •Шкала электромагнитных излучений
- •Интервалы длин волн видимого диапазона
- •Характеристики источников света5
- •Освещенность
- •Поглощение солнечного излучения поверхностью Земли
- •Удельная постоянная вращения7
- •Показатель преломления
- •Дисперсия показателя преломления (относительно воздуха)
- •Тема 7. Элементы квантовой физики атомов, молекул и твердых тел
- •Спектры излучения газов (l, нм)8
- •Тема 8. Основы квантовой физики атомного ядра и элементарных частиц
- •Масса покоя (m0) и энергия покоя (w0) элементарных частиц и легких ядер
- •Свойства радиоактивных изотопов
- •Предельные дозы облучения9
- •Реакции синтеза11
- •Термоядерные реакции во Вселенной12
- •Реакции деления урана
- •Характер фундаментальных взаимодействий
- •Классификация элементарных частиц13 по типу взаимодействия
- •Характеристики элементарных частиц
- •Стабильность элементарных частиц14
- •Свойства кварков
- •Кварковый состав адронов
- •Учебная литература основная учебная литература
- •Дополнительная учебная литература
Задачи по теме 6 для самостоятельного решения (кратность 10 - по № ф.И.О. Студента в журнале)
Температура внутренней поверхности печи при открытом отверстии площадью 30 см2 равна 1,3.103 К. Потребляемая мощность 1,5 кВт. Какая часть этой мощности теряется из-за теплового излучения стенками печи?
Красная граница фотоэффекта для некоторого металла 500 нм. Определить: работу выхода фотоэлектронов; максимальную скорость фотоэлектронов, вырываемых фиолетовым светом с длиной волны 400 нм.
На идеально отражающую поверхность (абсолютно белое тело) площадью 5 см2 за 3 мин нормально падает излучение с энергией 9 Дж. Определить: энергетическую освещенность поверхности; давление света на поверхность.
Фотон с энергией 1,025 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной комптоновской длине волны электрона 2,43 пм.
Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны 500 нм. Определить: температуру поверхности Солнца; энергию излучения за 10 мин; массу, теряемую Солнцем за это время.
Задерживающее напряжение для платиновой пластинки 3,7 В, а для другой (из неизвестного металла, но при тех же условиях) – 5,3 В. Определить работу выхода фотоэлектронов и вещество второй пластинки, если работа из первой 6,3 эВ.
Стенки 150-ваттной лампочки отражают 15% излучения нити накала. Определить давление света на стенки, считая лампочку сферическим сосудом радиуса 4 см.
После стрельбы внутренняя поверхность канала ствола 100-мм пушки нагрета до 227 0С. Вычислить мощность теплового излучения канала, считая его а.ч.т.
Какая доля энергии фотона приходится на электрон отдачи, если фотон испытал комптоновское рассеяние на угол 180 0? Энергия фотона до рассеяния 0,255 МэВ.
Поверхность калия освещается фиолетовым светом с длиной волны 400 нм. Определить наименьшее задерживающее напряжение для прекращения фототока, если работа выхода электронов их калия равна 2,0 эВ.
Вопросы по теме 6 для рефератов (все каждому студенту)
Эффект Комптона.
Закон Кирхгофа для равновесного теплового излучения.
Фотометрические величины. Температуры: радиационная, цветовая, яркостная.
Тема 7. Элементы квантовой физики атомов, молекул и твердых тел
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ по теме 7
Кинетическая энергия протона в 4 раза меньше его энергии покоя. Вычислить длину волны де Бройля.
 Дано:
Решение:
Дано:
Решение:
W0 /Wкин = 4 Длина волны де Бройля определяется отношением:
W0 = 1,50.10 –10 Дж l = h/p,
 где
h
–
постоянная Планка, p
– импульс протона.
где
h
–
постоянная Планка, p
– импульс протона.
l - ? Поскольку его кинетическая энергия сравнима с
энергией покоя, то движение - релятивистское, и импульс равен
![]() .
.
Следовательно, находим длину волны по формуле:
l = 4hc/(3W0);
l = 4.6,625.10-34.3.108/(3.1,50.10-10) = 1,77.10-15 (м).
Ответ: l = 1,77 Фм ("ферми").
Масса движущегося электрона в 3 раза больше его массы покоя. Чему равна минимальная неопределенность координаты электрона?
 Дано:
Решение:
Дано:
Решение:
m /m0 =3 Согласно соотношению неопределенности координаты и
m0 = 9,1.10-31 кг проекции импульса:
Dx.Dpx ³ h/2p ,
Dxmin - ? где h – постоянная Планка, а неопределенность импульса равна
.Dpx = m .DVx .
Скорость и ее неопределенность .DVx не могут превышать скорости света c. Поэтому
Dxmin = h/(2p mc).
С учетом данных условия получаем расчетную формулу:
Dxmin = h/(6p m0 c).
Проверим наименование единицы измерения координаты:
![]()
Вычислим неопределенность координаты:
![]()
Ответ: Dxmin = 1,28.10 -13 м.
Ч
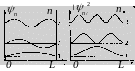 астица
находится в бесконечно глубокой
одномерной потенциальной прямоугольной
яме шириной L
на втором энергетическом уровне. В
каких точках плотность вероятности
обнаружения частицы совпадает с
классической плотностью вероятности?
астица
находится в бесконечно глубокой
одномерной потенциальной прямоугольной
яме шириной L
на втором энергетическом уровне. В
каких точках плотность вероятности
обнаружения частицы совпадает с
классической плотностью вероятности?
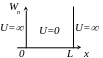 Дано:
Решение:
Дано:
Решение:
L, n = 2

x - ?
Решением уравнения Шредингера для волновой функции, описывающей состояние частицы в потенциальной яме, является выражение:
![]() ,
,
где
n
= 1, 2, … ¥
номер энергетического уровня (главное
квантовое число), x
– координата частицы (0£
x£
L).
Физический смысл имеет квадрат модуля
волновой функции как плотности вероятности
обнаружить частицу в точке с координатой
x:
![]() .
Для частицы на втором энергетическом
уровне плотность вероятности:
.
Для частицы на втором энергетическом
уровне плотность вероятности:
![]() .
.
Принцип соответствия Бора состоит в том, законы квантовой механики при больших значениях квантовых чисел (следовательно, при n®¥) переходят в законы классической физики. Для данной задачи это означает, что с ростом номера энергетического уровня последовательность уровней становится практически непрерывной, дискретность исчезает. Классическая плотность вероятности обнаружить частицу внутри потенциальной ямы шириной L равна w = 1/L. Приравнивая выражения для плотности вероятности, получим:
![]() ,
,
![]() ,
,
![]() ,
,
где k = 0, ±1, ±2,…
В пределах потенциальной ямы таких точек четыре: x = {L/8, 3L/8, 5L/8, 7L/8}
Ответ: x = {L/8, 3L/8, 5L/8, 7L/8}.
Определить: минимальную и максимальную энергии излучаемого фотона в видимой серии спектра водорода; первый потенциал и потенциал ионизации атома водорода.
n
Z
…
Состояние
ионизации
n
4
max





n
3
min



 стационарной
орбиты на другую,
стационарной
орбиты на другую,
W
2
 min
- ?
или с одного энергетического уровня
min
- ?
или с одного энергетического уровня
W
1
и
Серия Бальмера
max - ? на другой, атом излучает (илиj
1
j
 и
- ?
частоты,
соответствующей разности
и
- ?
частоты,
соответствующей разности
Серия Лаймана
Wki = h.nki = ½Wk – Wi½,
i – номер уровня, на который переходит электрон, k – номер уровня , с которого он переходит (при i < k фотон излучается, при i > k поглощается).
Для видимой части спектра водорода сериальные линии образуют серию Бальмера, для которой i = 2, k = 3,4,…(переход с 3-го, 4-го,… на 2-й уровень), а в ультрафиолетовой – серию Лаймана, для которой i = 1, k = 2, 3,…(переход со 2-го, 3-го,… на 1-й уровень). В серии Бальмера минимальная энергия излучается при переходе с 3-го на 2-й. Поэтому сериальная формула имеет вид:
![]() ,
,
где RH = 1,097.107 м -1 – постоянная Ридберга для водорода. Поскольку n = c/l, то
![]() ;
;
![]()
Фотон с максимальной энергией излучается при переходе ¥®2 :
![]() ;
;
![]() .
.
Атом возбуждается, если получает энергию извне, при этом электрон переходит на более высокий энергетический уровень. Потенциал, по определению, равен отношению потенциальной энергии к заряду. Первый потенциал возбуждения соответствует энергии перехода с 1-го на 2-ой уровень (в серии Лаймана):
![]() ,
,
где e = 1,6.10-19 Кл – заряд электрона. Этот потенциал равен
![]() .
.
В наиболее возбужденном состоянии атом теряет электрон и превращается в ион (ионизируется). Это происходит при переходе с 1-го на ¥-й уровень, и потенциал ионизации равен:
![]() ;
;
![]() .
.
Ответ: Wmin =1,89 эВ; Wmax = 3,41 эВ; j 1 = 10,2 В; j и = 13,6 В.
Температура Дебая некоторого кристалла 150 К. Определить: максимальную частоту кристаллической решетки; среднее число фононов с такой частотой, возбуждаемых при температуре 300 К.
Дано: Решение:
JD = 150 К Температура Дебая, ниже которой проявляются квантовые
T = 300 К свойства колебаний частиц в узлах кристаллической решетки
(существуют фононы) определяется формулой:
nmax - ? JД = h.nmax / k ,
![]() -
?
-
?
где h – постоянная Планка, nmax - максимальная частота колебаний, k - постоянная Планка. Следовательно, искомая частота равна:
nmax = k .JД / h;
nmax = 1,38.10-23 .150 / 6,625.10-34 = 3,12.1012 (Гц).
Фононы имеют целочисленный спин и подчиняются статистике Бозе – Эйнштейна, их среднее число в кантовом состоянии с энергией Wn определяется как
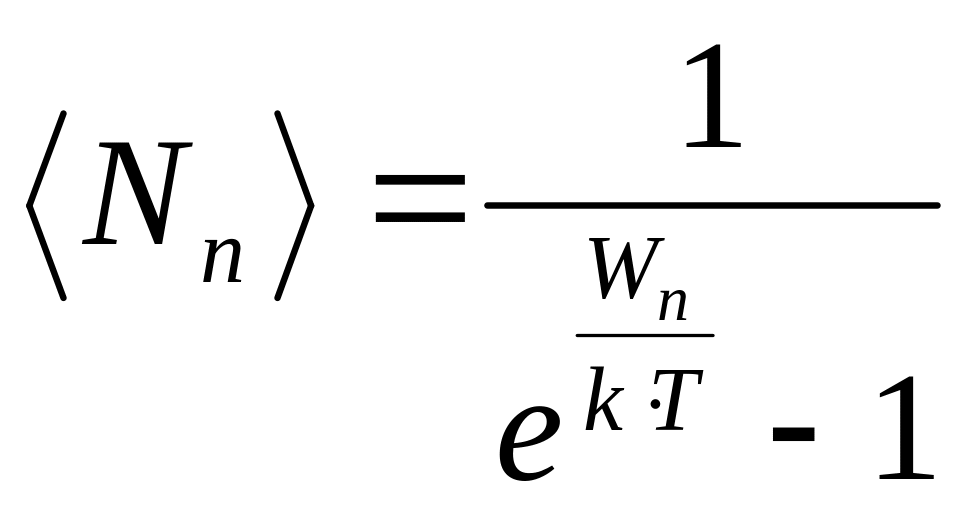 ,
,
где k – постоянная Больцмана, T - температура кристалла. Энергия фонона с частотой nmax равна
Wn = h.nmax = k .JД .
Таким образом, расчетная формула для :
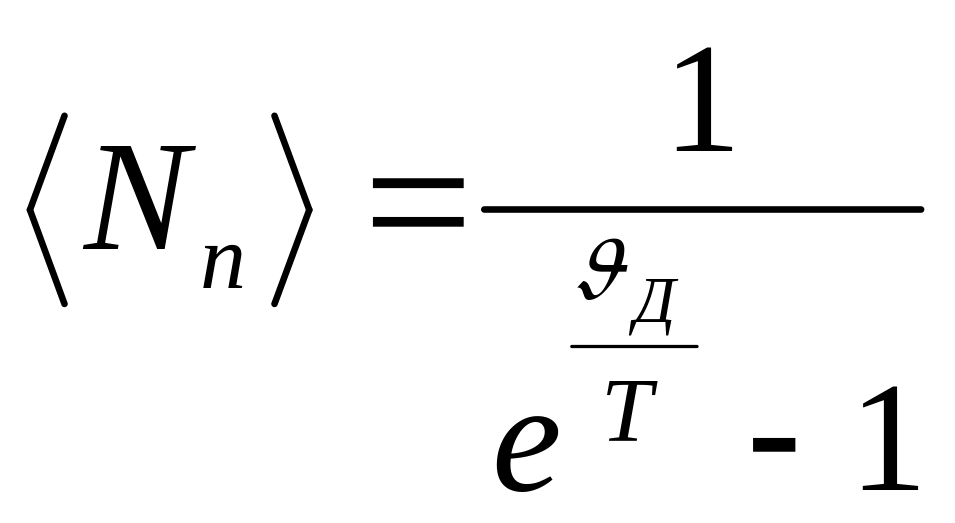 ;
;
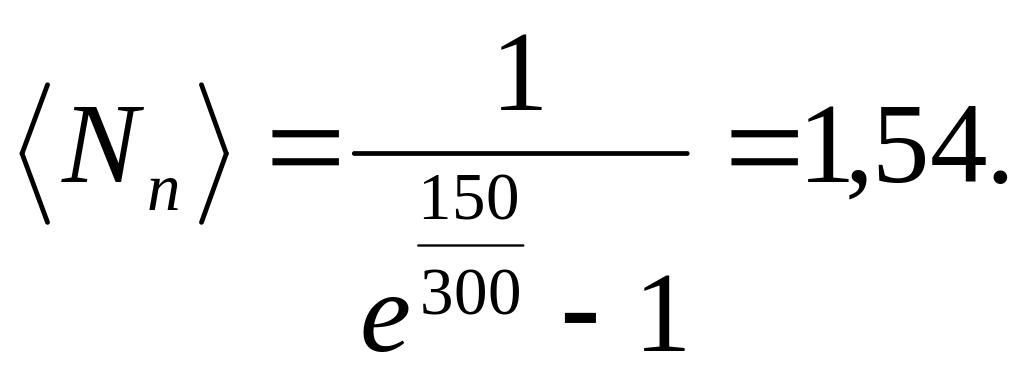
Ответ: nmax = 3,12.1012 Гц; = 1,54 фононов.
Определить работу выхода электронов из медного катода (эмиссионная постоянная 6 .105А/(м2 .К2) ), если при температура катода 2000 К плотность тока насыщения 3,64 мА/м2.
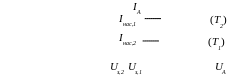 Дано:
Решение:
Дано:
Решение:
С = 6 .105А/(м2 .К2)
T = 2000 К =2.103 К
jнас = 3,64 мА/м2 =
= 3,64.10 -3 А/м2

Aвых - ?
Явление термоэлектронной эмиссия состоит в испускании нагретыми телами электронов из поверхностного слоя, термоэлектроны совершают работу выхода Aвых (против кулоновских сил притяжения) за счет энергии теплового движения (Для уменьшения работы выхода поверхность покрывают адсорбентами.) Термоэлектронная эмиссия применятся в электровакуумных приборах. Увеличение напряжения в цепи катода приводит к его нагреванию, а увеличение напряжения в цепи анода помогает термоэлектронам достичь анода и создать термоток. Когда все электроны достигают анода, ток насыщается. Плотность тока насыщения зависит от природы катода (работы выхода) и температуры, по формуле Ричардсона – Дешмана:
![]() ,
,
где k – постоянная Больцмана, С – эмиссионная постоянная. При увеличении температуры T катода плотность тока насыщения возрастает. Работы выхода зависит от природы и состояния поверхности катода. Найдем расчетную формулу:
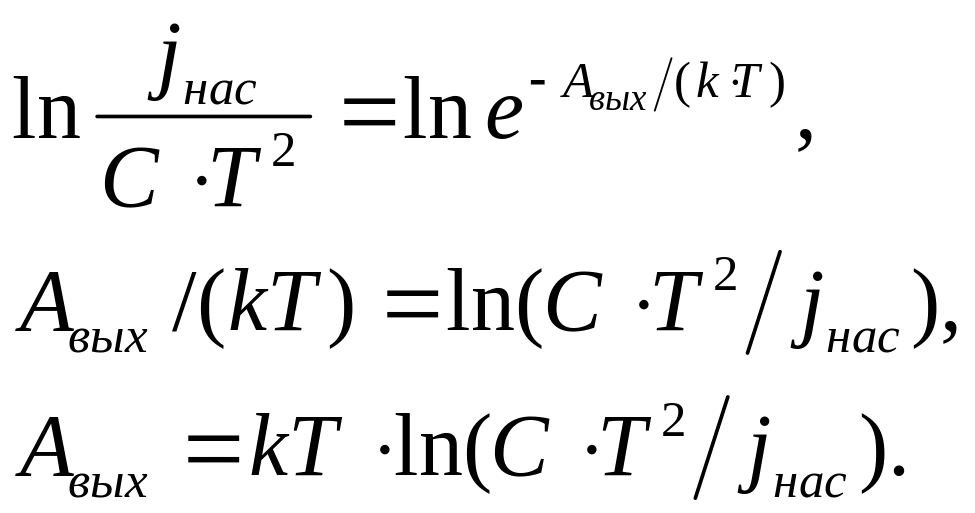 .
.
Вычислим работу выхода:
![]()
Ответ: Aвых = 3,64 эВ.
