12 Ответ.

Транспортная задача

Задача о размещении (транспортная задача) – это распределительная задача, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям–потребителям.

Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Исходные параметры модели ТЗ – количество пунктов отправления,

m – количество пунктов назначения,

ai – запас продукции в пункте отправления Ai ( i = 1,n ) [ед. прод.],

bj – спрос на продукцию в пункте назначения Bj (j = 1,m ) [ед. прод.],

cij – тариф (стоимость) перевозки единицы продукции из пункта отправления Ai в пункт назначения Bj [руб./ед. прод.].

Искомые параметры модели ТЗ

xij– количество продукции, перевозимой из пункта отправления Ai в пункт назначения Bj [ед. прод.].

L(X) – транспортные расходы на перевозку всей продукции [руб.].

Этапы построения модели

Определение переменных.

 Проверка сбалансированности задачи.

 Построение сбалансированной транспортной матрицы.

Задание целевой функции (ЦФ).

Задание ограничений.

Транспортная модель

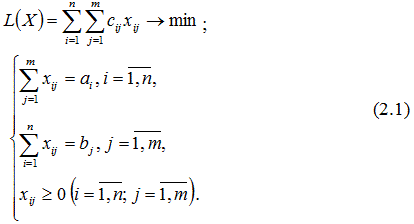
ЦФ представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица (табл. 2.1).

Таблица 2.1

Общий вид транспортной матрицы
Пункты отправления, Ai	Пункты потребления, Bi				Запасы, ед. прод.
	B1	B2	…	Bm
A1	c11 , [руб./ед. прод.]	c21	…	c1m	a1
A2	c21	c22	…	c2m	a2
…	…	…	…	…	…
An	cn1	cn2	…	cnm	am
Потребность ед. прод.	b1	b2	…	bm

Из модели (2.1) следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е.

(2.2)

Если (2.2) выполняется, то ТЗ называется сбалансированной (закрытой), в противном случае – несбалансированной (открытой). В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный (реально не существующий) пункт потребления, который будет формально потреблять существующий излишек запасов, т.е.

Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:

Для фиктивных перевозок вводятся фиктивные тарифы cф, величина которых обычно приравнивается к нулю cф=0. Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина cф может быть любым положительным числом.

Пример.

Методы нахождения опорных планов

Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. "Качество" опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла – наихудшее.

Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована.

Метод северо-западного угла 

На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов.

Для того чтобы заполнить клетку (i,j), необходимо сравнить текущий запас товара в рассматриваемой i–й строке aiтек с текущей потребностью в рассматриваемом j–м столбце bjтек.

Если существующий запас позволяет перевезти всю потребность, то

в клетку (i,j) в качестве перевозки вписывается значение потребности bjтек;

j–й столбец вычеркивается, поскольку его потребность уже исчерпана;

от существующего запаса в i–й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е. (aiтек – bjтек)

Если существующий запас не позволяет перевезти всю потребность, то

в клетку (i,j) в качестве перевозки вписывается значение запаса aiтек

i–я строка вычеркивается, поскольку ее запас уже исчерпан;

от существующей потребности в j–й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е. (bjтек – aiтек)

Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы.

Метод минимального элемента 

На каждом шаге метода минимального элемента из всех не вычеркнутых клеток транспортной матрицы выбирается клетка с минимальной стоимостью перевозки min сij. Заполнение выбранной клетки производится по правилам, описанным выше.

Метод Фогеля 

На каждом шаге метода Фогеля для каждой i–й строки вычисляются штрафы di как разность между двумя наименьшими тарифами строки. Таким же образом вычисляются штрафы di для каждого j–го столбца. После чего выбирается максимальный штраф из всех штрафов строк и столбцов. В строке или столбце, соответствующем выбранному штрафу, для заполнения выбирается не вычеркнутая клетка с минимальным тарифом min cij

Если существует несколько одинаковых по величине максимальных штрафов в матрице, то в соответствующих строках или столбцах выбирается одна не вычеркнутая клетка с минимальным тарифом min cij.

Если клеток с минимальным тарифом также несколько, то из них выбирается клетка (i,j) с максимальным суммарным штрафом, т.е. суммой штрафов по i–й строке и j–му столбцу.

Формально и реальные и фиктивные столбцы и строки в транспортной матрице абсолютно равноправны. Поэтому при нахождении опорных планов фиктивные строки, столбцы и тарифы необходимо анализировать и использовать точно так же как и реальные. Но при вычислении значения ЦФ фиктивные перевозки не учитываются, поскольку они реально не были выполнены и оплачены.

Если величина фиктивных тарифов превышает максимальный из реальных тарифов задачи [cф > max cij (i=1,n; j=1,m)], то методы минимального элемента и Фогеля позволяют получить более дешевые планы перевозок, чем в случае с нулевыми фиктивными тарифами.

Пример.

Метод Потенциалов 

Для определения оптимального плана транспортной задачи разработано несколько методов. Однако наиболее часто используются метод потенциалов и метод дифференциальных рент.

Метод потенциалов. Общий принцип определения оптимального плана транспортной задачи методом потенциалов аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.

Для определения опорного плана транспортной задачи будем пользоваться одним из методов: северо-западного угла, минимального элемента и Фогеля.

Эти методы гарантируют получение занятых в исходной таблице условий n+m–1 клеток, причем в некоторых из них могут стоять, нули. Полученный план следует проверить на оптимальность.

Теорема. Если для некоторою опорного плана X*=(х*ij) (i=1,2,…, m; j=1,2,…, n) транспортной задачи существуют такие числа a1, a2, …, am, β1, β2,…, βn, что

βj – ai = cij при хij > 0,

βj – ai ≤ cij при хij = 0

для всех i=1,2,…, m; j=1,2,…, n, то X*=(х·хij) – оптимальный план транспортной задачи.

Числа ai и βj (i=1,2,…, m; j=1,2,…, n) называются потенциалами соответственно пунктов назначения и пунктов потребления.

Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы ai и βj(i=1,2,…, m; j=1,2,…, n). Эти числа находят из системы уравнений

βj – ai = cij,

(2.3)

где cij – тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.

Так как число заполненных клеток равно n + m – 1, то система (2.3) с n + m неизвестными содержит n + m – 1 уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например a1 = 0, и найти последовательно из уравнений (2.3) значения остальных неизвестных. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа aij = βi – ai – cij.

Если среди чисел aij нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки  aij > 0, то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых aij > 0, и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.

Заполняя выбранную клетку, необходимо изменить объемы поставок, Записанных в ряде других занятых клеток и связанных с заполненной так называемым циклом.

Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами. Примеры некоторых циклов показаны на 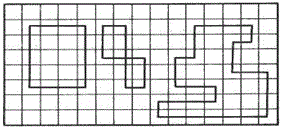рис. 2.1.

Рис. 2.1

При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных циклом с данной свободной клеткой. Это перемещение производят по следующим правилам:

каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке – знак плюс, а всем остальным клеткам – поочередно знаки минус и плюс (будем называть эти клетки минусовыми и плюсовыми);

в данную свободную клетку переносят меньшее из чисел стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел считается свободной. В результате указанных выше перемещений грузов в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи.

Описанный выше переход от одного опорного плана транспортной задачи к другому ее опорному плану называется сдвигом по циклу пересчета.

Следует отметить, что при сдвиге по циклу пересчета числа занятых клеток остается неизменным, а именно остается равным n + m – 1. При этом если в минусовых клетках имеется два (или более) одинаковых числа хij, то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками).

Полученный новый опорный план транспортной задачи проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа  a'ij = β'j – a'i – cij для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.

В заключение отметим, что при определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать в этом случае зацикливания, следует соответствующие нулевые элементы опорного плана заменить сколь угодно малым положительным числом εи решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать ε равным нулю.