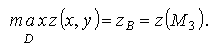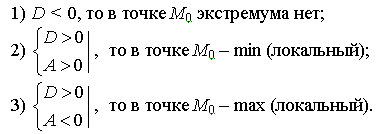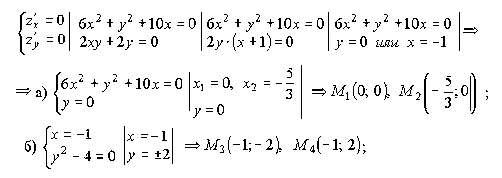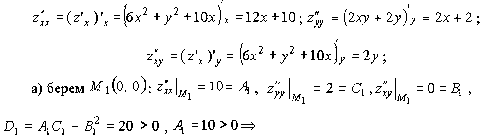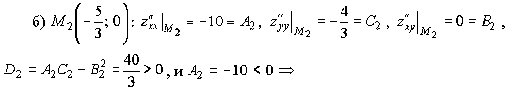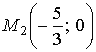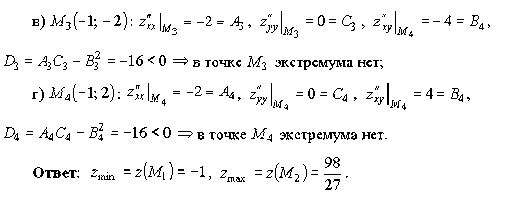1 ответ
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. Вматематическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Пусть дана
функция ![]() и
и ![]() —
внутренняя точка области определения
—
внутренняя точка области определения ![]() Тогда
Тогда
![]() называется
точкой локального максимума функции
называется
точкой локального максимума функции ![]() если
существует проколотая окрестность
если
существует проколотая окрестность ![]() такая,
что
такая,
что
![]()
называется точкой локального минимума функции если существует проколотая окрестность такая, что
![]()
Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.
называется точкой абсолютного (глобального) максимума, если
![]()
называется точкой абсолютного минимума, если
![]()
Значение
функции ![]() называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Замечание
Функция
определённая
на множестве ![]() может
не иметь на нём ни одного локального
или абсолютного экстремума. Например,
может
не иметь на нём ни одного локального
или абсолютного экстремума. Например, ![]()
Необходимые условия существования локальных экстремумов
Из леммы Ферма вытекает следующее:
Пусть точка
является
точкой экстремума функции ![]() ,
определенной в некоторой окрестности
точки
.
,
определенной в некоторой окрестности
точки
.
Тогда либо
производная ![]() не
существует, либо
не
существует, либо ![]() .
.
(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)
Достаточные условия существования локальных экстремумов
Пусть функция ![]() непрерывна
в
непрерывна
в ![]() и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные ![]() .
Тогда при условии
.
Тогда при условии
![]()
является точкой строгого локального максимума. А если
![]()
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
Пусть функция непрерывна и дважды дифференцируема в точке . Тогда при условии
и ![]()
является точкой локального максимума. А если
и ![]()
то является точкой локального минимума.
|
3 Ответ
2.5 Скалярное поле. Поверхности и линии уровня
Рассмотрим
в 3-х мерном пространстве некоторую
область. Если в каждой точке ![]() этой
области задать число (скаляр)
этой
области задать число (скаляр) ![]() ,
то говорят, что задано скалярное поле
.
Согласно такому определению, скалярное
поле является функцией точки. Так как
положение точки
можно
характеризовать ее радиус-вектором
,
то говорят, что задано скалярное поле
.
Согласно такому определению, скалярное
поле является функцией точки. Так как
положение точки
можно
характеризовать ее радиус-вектором ![]() ,
то задание поля будет означать, что
установлено соответствие между
и
.
Таким образом, поле можно рассматривать
как функцию векторного аргумента
,
то задание поля будет означать, что
установлено соответствие между
и
.
Таким образом, поле можно рассматривать
как функцию векторного аргумента ![]() (рис. 13).
(рис. 13).
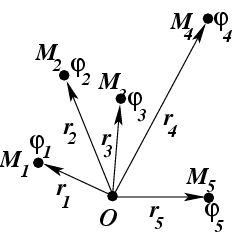
Рис.13. К определению скалярного поля
Если
в области определения поля ввести
декартову систему координат, то
можно
представить как упорядоченную тройку
чисел ![]() и
тогда задание поля будет эквивалентно
заданию функции трех переменных
и
тогда задание поля будет эквивалентно
заданию функции трех переменных ![]() .
В дальнейшем будем считать эту функцию
непрерывной и дифференцируемой.
.
В дальнейшем будем считать эту функцию
непрерывной и дифференцируемой.
Как
известно, функцию одной переменной
можно рассматривать как уравнение
кривой на плоскости ![]() ,
двух переменных - как поверхность
,
двух переменных - как поверхность ![]() .
Представить аналогичный "график"
в случае поля
.
Представить аналогичный "график"
в случае поля ![]() затруднительно,
поэтому для наглядной характеристики
поля используютповерхности уровня.
затруднительно,
поэтому для наглядной характеристики
поля используютповерхности уровня.
Поверхностью
уровня поля ![]() называют
геометрическое место точек, в которых
поле принимает постоянное значение.
Согласно такому определению, уравнение
поверхности уровня будет иметь вид:
называют
геометрическое место точек, в которых
поле принимает постоянное значение.
Согласно такому определению, уравнение
поверхности уровня будет иметь вид:
|
(61) |
Уравнение (61)
является уравнением поверхности, что
объясняет соответствующее название.
Придавая ![]() различные
значения, можно получить наглядное
представление о том, как величина
распределена
в пространстве. При этом, если в некоторой
области поле изменяется быстро,
поверхности уровня будут сближаться.
Пересекаться они не могут, за исключением
одной точки.
различные
значения, можно получить наглядное
представление о том, как величина
распределена
в пространстве. При этом, если в некоторой
области поле изменяется быстро,
поверхности уровня будут сближаться.
Пересекаться они не могут, за исключением
одной точки.
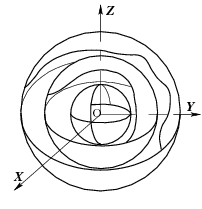
Рис.14. Поверхности уровня скалярного поля.
Пр. Рассмотрим
поле вида ![]() (или
просто
(или
просто ![]() ).
Уравнение (61)
принимает вид:
).
Уравнение (61)
принимает вид:
![]()
Так как ![]() ,
то
,
то
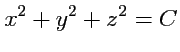
и, таким образом, поверхностями уровня поля будет семейство концентрических сфер с центром в начале координат (рис. 14).
ПР. Построить линии
уровня плоского поля 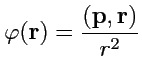 ,
где
,
где ![]() ,
, ![]() ,
, ![]() (2-х
мерный аналог потенциала электрического
диполя).
(2-х
мерный аналог потенциала электрического
диполя).
Решение. Уравнение линий уровня имеет вид:
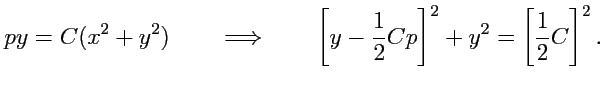
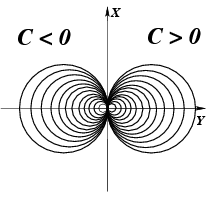
Рис.15. Линии уровня плоского поля.
Для различных
значений
получается
семейство окружностей с единственной
общей точкой в начале координат (рис. 15).
В левой полуплоскости значения поля
положительно, в правой - отрицательно,
а в точке ![]() поле
имеет особенность и неопределено.
поле
имеет особенность и неопределено.
4 Ответ.
Производная по направлению
Пусть снова
функция ![]() задана
в области
задана
в области ![]() и
имеет во всех точках
и
имеет во всех точках ![]() частные
производные по всем переменным
частные
производные по всем переменным ![]() .
Предположим, что все частные
производные
.
Предположим, что все частные
производные 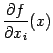 непрерывны
в точке
непрерывны
в точке ![]() .
Тогда функция
длифференцируема
в точке
.
Тогда функция
длифференцируема
в точке ![]() ,
то есть приращение функции
,
то есть приращение функции![]() имеет
главную линейную часть, которая равна
дифференциалу:
имеет
главную линейную часть, которая равна
дифференциалу: ![]() где
где ![]() --
величина большего порядка малости
при
--
величина большего порядка малости
при ![]() ,
чем
,
чем ![]() .
Напомним, что
.
Напомним, что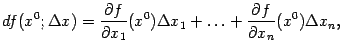 так
что получаем
так
что получаем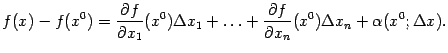 (
8 .1) Фиксируем теперь в
(
8 .1) Фиксируем теперь в ![]() какое-нибудь
направление, выбрав задающий его
ненулевой вектор
какое-нибудь
направление, выбрав задающий его
ненулевой вектор![]() Через
точку
в
направлении вектора
Через
точку
в
направлении вектора ![]() проходит
некоторая ось
проходит
некоторая ось ![]() .
(Напомним, что осью называется прямая
с выбранным на ней направлением, то есть
выбранным порядком следования точек.)
Точки
.
(Напомним, что осью называется прямая
с выбранным на ней направлением, то есть
выбранным порядком следования точек.)
Точки ![]() этой
оси можно задать параметрическими
уравнениями:
этой
оси можно задать параметрическими
уравнениями: ![]() или,
в векторном виде,
или,
в векторном виде, ![]() ,
где
,
где ![]() и
увеличению значений параметра
и
увеличению значений параметра ![]() соответствует
движение точки
соответствует
движение точки ![]() оси
в
направлении вектора
.
Обозначим
оси
в
направлении вектора
.
Обозначим ![]() ту
часть оси
,
которая состоит из точек оси, следующих
после
,
то есть точек луча
ту
часть оси
,
которая состоит из точек оси, следующих
после
,
то есть точек луча![]() ,
получающегося при
,
получающегося при ![]() .
Определение
8 . 2 Значение предела
.
Определение
8 . 2 Значение предела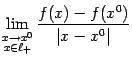 называется
производной функции
по
направлению оси (или луча )
(или
по направлению вектора
),
вычисленной в точке
.
Производная по направлению
обозначается
называется
производной функции
по
направлению оси (или луча )
(или
по направлению вектора
),
вычисленной в точке
.
Производная по направлению
обозначается 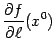 или
или  Смысл определения производной по
направлению -- в том, что она задаёт
мгновенную скорость изменения значений
функции
при
прямолинейном и равномерном движении
точки
Смысл определения производной по
направлению -- в том, что она задаёт
мгновенную скорость изменения значений
функции
при
прямолинейном и равномерном движении
точки ![]() вдоль
оси
в
момент
вдоль
оси
в
момент ![]() .
Заметим, что если направление
оси
совпадает
с направлением одной из координатных
осей
.
Заметим, что если направление
оси
совпадает
с направлением одной из координатных
осей ![]() ,
то производная функции
,
то производная функции ![]() по
такому направлению, очевидно, равняется
(правой) производной функции
по
соответствующей переменной
.
Если существует (двусторонняя) частная
производная по
,
то получаем, что
по
такому направлению, очевидно, равняется
(правой) производной функции
по
соответствующей переменной
.
Если существует (двусторонняя) частная
производная по
,
то получаем, что 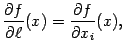 если
если ![]() .
Используя параметризацию точки на
луче
вида
.
Используя параметризацию точки на
луче
вида ![]() и
замечая, что условие
и
замечая, что условие![]() означает,
что
означает,
что ![]() ,
получаем:
,
получаем: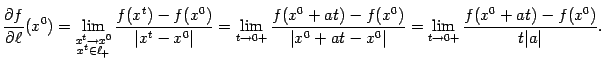 Запишем
теперь приращение функции, стоящее в
числителе, через частные производные
с помощью формулы ( 8.1 ):
Запишем
теперь приращение функции, стоящее в
числителе, через частные производные
с помощью формулы ( 8.1 ):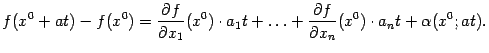 Отсюда
Отсюда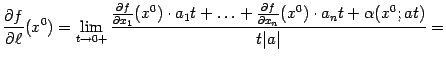
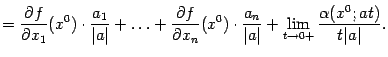 Здесь в правой части первые
Здесь в правой части первые ![]() слагаемых
не зависят от
.
Поскольку
слагаемых
не зависят от
.
Поскольку ![]() при
,
то последний предел равен 0, так как
--
величина большего порядка малости,
чем
.
Итак, получили формулу
при
,
то последний предел равен 0, так как
--
величина большего порядка малости,
чем
.
Итак, получили формулу 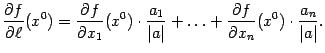 С
помощью этой формулы можно вычислять
производную по любому направлению, если
известен направляющий вектор этого
направления
.
Заметим, что в правой части полученной
формулы первый множитель каждого
слагаемого -- это компонента вектора
С
помощью этой формулы можно вычислять
производную по любому направлению, если
известен направляющий вектор этого
направления
.
Заметим, что в правой части полученной
формулы первый множитель каждого
слагаемого -- это компонента вектора![]() ,
а второй множитель -- компонента
вектора
,
а второй множитель -- компонента
вектора ![]() .
Этот вектор лишь длиной отличается от
вектора
;
направление его, очевидно, то же, что
у
.
Длина вектора
.
Этот вектор лишь длиной отличается от
вектора
;
направление его, очевидно, то же, что
у
.
Длина вектора ![]() равна
1:
равна
1: 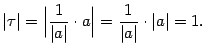 Поэтому
компоненты вектора
Поэтому
компоненты вектора ![]() --
это направляющие косинусы -- косинусы
углов
--
это направляющие косинусы -- косинусы
углов ![]() между
осью
и
осями координат
:
между
осью
и
осями координат
: ![]() где
где ![]() --
единичный направляющий вектор оси
,
--
единичный направляющий вектор оси
, ![]() ,
а точкой
,
а точкой ![]() обозначено
скалярное произведение векторов
и
.
Таким образом, имеет место следующая
теорема, выражающая связь между
производной по направлению, градиентом
и единичным направляющим вектором оси:
Теорема 8 . 1
Если все частные
производные
обозначено
скалярное произведение векторов
и
.
Таким образом, имеет место следующая
теорема, выражающая связь между
производной по направлению, градиентом
и единичным направляющим вектором оси:
Теорема 8 . 1
Если все частные
производные ![]() функции
непрерывны
в точке
и
направление оси
задано
вектором
функции
непрерывны
в точке
и
направление оси
задано
вектором ![]() ,
то
,
то 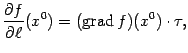 где
где![]() --
единичный направляющий вектор оси
,
или
--
единичный направляющий вектор оси
,
или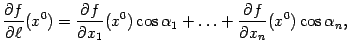 где
где ![]() --
углы между осью
и
осями
--
углы между осью
и
осями ![]() .
.