1. 18. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница для вычисления определенного интеграла. Замена переменных в определенном интеграле.

Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница для вычисления определенного интеграла.

Интеграл как функция верхнего предела.

Для функции  , интегрируемой для всех   , значение интеграла   зависит от значения верхнего предела  ; можно рассмотреть функцию переменной  : каждому значению   ставится в соответствие число, равное значению интеграла   . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела:  ; функция  определена в области интегрируемости подынтегральной функции  . Если  —первообразная для  , то значение  можно вычислить по формуле Ньютона—Лейбница: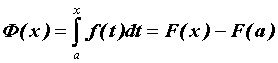  . Функцию   можно исследовать, не вычисляя первообразной. Для интегрируемой при  функции  справедливы следующие утверждения:   непрерывна на промежутке  , причем  ; если  при  , то      монотонно возрастает на промежутке  ; если  непрерывна при  , то  дифференцируема на промежутке  , причем .

Замена переменных в определенном интеграле.

Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.

     В таком случае

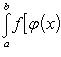
     (22)

     Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.

     Переходя к доказательству теоремы, обозначим интегралы, входящие в левую и правую части формулы (22), соответственно черезI_лев и I_прав.

     Пусть F(z) - функция первообразная для f(z). Тогда по формуле Ньютона-Лейбница/p>

I_прав = F[φ(b)] - F[φ(a)].     (23)

Что же касается I_лев, то

Но согласно теореме будет

Значит,

I_лев = F[φ(b)] - F[φ(a)].

Отсюда и из (23) следует, что I_лев = I_прав.

19. Несобственный интеграл с неограниченной областью интегрирования. Несобственный интеграл от функции, неограниченной на отрезке интегрирования. Понятие сходимости несобственных интегралов.

Несобственные интегралы с бесконечными пределами интегрирования

   Пусть функция y = f(x) определена и интегрируема на произвольном отрезке [а, t], т.е. функция

определена для произвольного значения t ≥ a. Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел

                        (9.1)

   Если предел, стоящий в правой части равенства (9.1), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае — расходящимся.    Выделяют следующие две задачи: а) исследование вопроса о сходимости заданного несобственного интеграла; б) вычисление значения интеграла в случае, если несобственный интеграл сходится. В некоторых случаях решения этих двух задач удается объединить.    По аналогии с (9.1) определяется несобственный интеграл на полуинтервале (-∞, b]:

                        (9.2)

Определение сходимости интеграла   аналогично приведенному выше.    Несобственный интеграл на интервале (-∞ , +∞) определяется следующим образом

                        (9.3)

   Интеграл   называется сходящимся, если существует конечный предел справа как предел функции двух переменных. Если предела нет, то несобственный интеграл   называется расходящимся.

Несобственный интеграл от функции, неограниченной на отрезке интегрирования.