16. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла.

Рассмотрим функцию f(х), определенную в каждой точке сегмента      [а, b]. Введем понятия разбиения сегмента [а, b], измельчения этого разбиения и объединения двух разбиений.

Определение 1. Будем говорить, что задано разбиение сегмента [а, b], если заданы точки х₁, x₂,..., х_п такие, что а= х₁<x₂<...<х_п= b, Разбиение сегмента [а, b] будем в дальнейшем обозначать символом {х_k}.

Определение 2. Разбиение {х΄_k} сегмента [а, b] называется измельчением разбиения {х_k} того же сегмента, если каждая точка х_p разбиения {х_k} совпадает с одной из точек х_q разбиения {х΄_k}.

Определение 3. Разбиение {х_k} сегмента [а, b] называется объединением разбиений {х΄_k} и {х"_k} того же сегмента, если все точки разбиений {х΄_k} и {х"_k} являются точками разбиения {х_k} и других точек разбиение {х_k} не содержит.

Заметим, что объединение двух разбиений является измельчением каждого из них.

Рассмотрим на сегменте [а, b] функцию f(х), принимающую в каждой точке сегмента конечные значения. По данному разбиению {х_k} построим число, так называемую «интегральную сумму»,

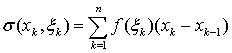, где _k— некоторая точка сегмента

[х_k-1, х_k]. Подчеркнем, что интегральная сумма   зависит как от разбиения {х_k}, так и от выбора точек _k на сегментах [х_k-1, х_k]. Если обозначить через х_k  разность х_k -х_k-1, то интегральную сумму, в дальнейшем часто обозначаемую просто через , можно записать и так:

.

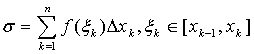Сегменты [х_k-1, х_k] иногда называют частичными сегментами, а точки   _k — промежуточными точками.

Число d = mах х_k  договоримся называть диаметром разбиения {х_k}.

Введем фундаментальные понятия предела интегральных сумм и интегрируемости функции по Риману.

Определение 4. Число I  называется пределом, интегральных сумм   при стремлении диаметра d разбиений {х_k} к нулю, если для всякого  >0 существует, такое число  = ( )>0, что из условия d<  при любом выборе промежуточных точек _k следует неравенство | I - | <  .

Легко убедиться в том, что может существовать только один предел интегральных сумм   при d0.

Для обозначения предела интегральных сумм употребляют символ

.

Определение 5. Функция f(х) называется интегрируемой по Риману на сегменте [а, b], если для этой функции на указанном сегменте существует предел I  ее интегральных сумм   при стремлении диаметра d  разбиений

{х_k} к нулю.

Число I  называется определенным интегралом Римана от функции f(х) в пределах от а до b и обозначается символом

.

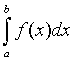Таким образом, по определению 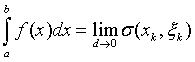 . Отметим, что

число а называют нижним пределом интегрирования, а число b - верхним пределом интегрирования. Переменную x под знаком определенного интеграла можно заменить на любую другую переменную, т.е. справедливы равенства

  

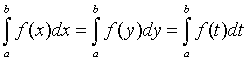
Геометрический смысл определенного интеграла.

Определённый интеграл 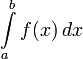  численно равен площади фигуры, ограниченной осью абсцисс, прямыми   и   и графиком функции  .

17.Основные свойства определенного интеграла. Теорема о среднем.

сновные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.

     Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то

т. е. интеграл суммы равен сумме интегралов слагаемых.

     В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь

после чего остается перейти к пределу при λ → 0.

     Аналогично доказывается

     Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то

т. е. постоянный множитель можно выносить за знак интеграла.

     Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.

     В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = x_m, то

     Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.

Теорема о среднем.

 Если f(x) непрерывна на отрезке [a,b], то существует точка  , такая что 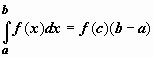 .  Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда 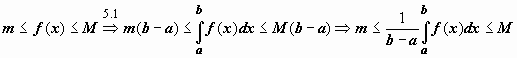 . Число 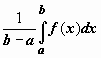  заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка  , такая что 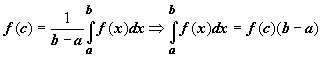 .  Это свойство имеет простую геометрическую интерпретацию: если   непрерывна на отрезке [a,b], то существует точка   такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c)