3.8. Алгоритмы управления проектами.

Обучение в школе или подготовка специалиста в институте, разработка документации на автоматизированное рабочее место или автоматизированную систему управления, строительство сооружений включает в себя большое количество операций (работ) и большое количество исполнителей этих работ. Условно объединим эти виды деятельности под общим понятием - проект. Тогда задача управления проектом состоит в том, чтобы с учетом взаимосвязей работ и необходимости исполнения каждой работы завершить исполнение проекта в заданные сроки и с заданными затратами трудовых, финансовых или материальных ресурсов.

Для управления проектом разработан метод сетевого планирования и управления (СПУ), в основу которого положен метод критического пути (МКП). Этот метод позволяет:

1) планировать работу над проектом и предвидеть возможные затруднения и задержки в исполнении каждой работы и проекта в целом;

2) координировать и контролировать исполнение работ всеми исполнителями в заданные сроки и при заданном ресурсном обеспечении;

3) устанавливать последовательность и сроки использования ограниченных ресурсов в течении всего времени исполнения проекта;

4) выполнять анализ компромиссных решений между затратами и сроками выполнения работ с учетом резерва времени;

5) планировать ускоренное завершение всего проекта с учетом исполнения всех работ.

Каждый проект должен иметь перечень всех работ, продолжительность исполнения каждой работы, перечень работ, непосредственно предшествующих и определяющих начало каждой операции.

Граф типа сеть является идеальным образом исполнения проекта. В этом графе одна вершина-исток, определяющая начало исполнения проекта, одна вершина-сток, формирующая окончание исполнения проекта, множество дуг, характеризующих работы по продолжительности исполнения или по затратам трудовых или финансовых ресурсов (_ij), множество событий, фиксирующих начало и окончание каждой работы, комплекса работ или проекта в целом. Комплекс работ характерен наличием нескольких дуг заходящих или исходящих из данной вершины. В сетевом графе не должно быть петель и контуров.

Рассмотрим фрагмент графа (см. рис. 50), включающий в себя пять вершин-событий и шесть дуг-работ. х₀-начало проекта, х_k-окончание проекта, ₀₁ и ₀₂- работы, которые могут быть начаты с началом работ над проектом. Событие х₁ есть окончание работы ₀₁ и определяет начало комплекса работ ₁₂ и ₁₃. Событие х₂ есть окончание комплекса работ ₀₂ и ₁₂ и определяет начало работ _2k. Событие х₃ есть окончание работы ₁₃ и определяет начало работы _3k, и наконец, работы _2k и _3k обеспечивают завершение проекта, которые могут быть начаты только после окончание работ ₁₂, ₁₃, ₀₂ и ₀₁. Итак, существует три различных пути на графе, которые должны быть пройдены для завершение всех работ проекта:

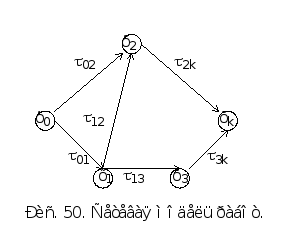
1) (₀₂+_2k);

2) (₀₁+₁₂+_2k);

3) (₀₁+₁₃+_3k).

Продолжительность работ на каждом пути различная. Наибольшая продолжительность есть критический путь для всего проекта, т.к. только он определяет продолжительность исполнения всего проекта. Работы на критическом пути не допускают никакой задержки в исполнении. Поэтому их также называют критическими работами. Для критических работ и критического пути нет резерва времени.

tp(х1)=4 x1 1,4=6 tp(х2)=7 tp(х4)=12 x2 2,4=5 x4 tp(х3)=5 3,4=3 x3

tp(х3)=5 3,4 tp(х2)=7 2,4 tp(х1)=4 1,4 5 10 t

Рис. 51. Ранний момент наступления события.

Так как каждое событие характеризуется временем его наступления, то при наличии комплекса работ для события х_i можно рассматривать ранний момент наступления события t_p(х_i) и поздний момент наступления события t_n(х_i). Для иллюстрации определения t_p(х_i) и t_n(х_i) рассмотрим фрагмент сети (см. рис. 51 и 52). На рис. 51 события х₁, х₂ и х₃ пусть имеют ранние моменты наступления: t_p(х₁)=4; t_p(х₂)=7; t_p(х₃)=5, т.е. любые работы, которые предшествовали событиям х₁, х₂ и х₃, оказались законченными к указанным моментам времени t_p(х₁), t_p(х₂), t_p(х₃). Ранний момент наступления события t_p(х₄) определяется наиболее поздним окончанием одной из работ, предшествующих этому событию, т.е. (4+6)=10; (7+5)=12; (5+3)=8. Следовательно t_p(х₄)=12.

Обобщая эти рассуждения, можно сделать заключение:

t_p(х_j)=max_i{(t_p(х_i)+_i,j)}, где

t_p(х_j)-ранний момент наступления события х_j;

t_p(х_i)-ранние моменты наступления событий х_i, определяющих начало работ, непосредственно предшествующих событию х_j;

_i,j-продолжительность работы, предшествующей событию х_j;

Таким образом, если для начального события х₀ принять известным ранний момент наступления события (например, t_p(х₀)=0), то можно найти ранние моменты наступления всех последующих событий до х_k включительно.

На рис. 52 события х₂, х₃ и х₄ имеют поздние допустимые моменты наступления t_n(х₂), t_n(х₃), t_n(х₄), т.е. работы ₁₂, ₁₃ и ₁₄ должны быть закончены не позднее наступления t_n(х₂), t_n(х₃), t_n(х₄). Следовательно, при оценке позднего момента наступления t_n(х₁) события необходимо искать наиболее протяженные пути от конца проекта, т.е. продвигаяться в обратном направлении. Поздний момент наступления события х₁ определяется наименьшим значением начала одной из работ, следующих после события х₁, т.е. (12-7)=5; (15-7)=8; (10-3)=7. Следовательно, t_n(х₁)=5.

tn(х2)=12 х2 1,2=7 tn(х1)=5 1,3=7 tn(х3)=15 х1 х3 1,4=3 tn(х4)=10 х4

tn(х3)=15 1,3 tn(х2)=12 1,2 tn(х4)=10 1,4 t 5 10 15

Рис. 52. Поздний момент наступления события.

Обобщая эти рассуждения можно сделать заключение:

t_n(х_j)=min_i{(t_n(х_i)-_j,i)}, где

t_n(х_j)-поздний момент наступления события х_j, определяющего начало работ _j,i;

t_n(х_i)-поздний момент наступления событий х_i, определяющего окончание работы _j,i;

_j,i-продолжительность работы _j,i, обусловленной событием х_j.

Таким образом, если для конечного события х_k принять известным поздний момент наступления события (например, t_n(х_k)=t_p(х_k)), то можно найти поздний момент наступления всех предшествующих событий до х₀ включительно.

Особое место в анализе сетевых графиков занимают фиктивные работы, к которым можно отнести ожидание. На рис. 53 дан фрагмент сети с ожиданием для одновременного исполнения работ ₃₅ и ₄₆.

tp(х1)=5 tp(х3)=10 х1 1,3=5 х3 3,5=4 х5 tp(х2)=2 tp(х4)=10 х2 2,4=6 х4 4,6=5 х6

2,4 4,6 tт(х6)=15 1,3 3,5 tт(х2)=15 tp(х1)=5 1,3 3,5 2,4 4,6 tp(х2)=2 t 5 10

Рис. 53. Фиктивная работа-ожидание.

Фиктивная работа имеет продолжительность равную нулю, но события связанные с ожиданием (х₃, х₄ на рис. 53) обуславливают возможность только одновременного начала работ (₃₅ и ₄₆ на рис. 53). На сетевых графах ожидание обозначают пунктирной линией. При расчетах раннего и позднего моментов наступления событий, связанных с ожиданием (х₃, х₄ на рис. 53), используют вышеприведенные соотношения, т.е.

t_p^ожид.(х₃;х₄)=max{t_p(х₃); t_p(х₄)},

t_n^ожид.(х₃;х₄)=min{t_n(х₃); t_n(х₄)}.

Максимально время, на которое можно задержать наступление некоторого события без задержки срока завершения всего проекта, называют резервом времени для данного события. Поэтому для каждого события резерв времени есть t₀(х_i)=t_n(х_i)- t_p(х_i).

Если наиболее поздний и наиболее ранний сроки наступления события х_i одинаковы, то задержка наступления этого события не допускается. Событие с нулевым резервом времени находятся на критическом пути, соединяющим начальную и конечную вершины сетевой модели проекта.

Критический путь представляет собой взаимосвязную последовательность работ и событий, имеющих нулевой резерв времени. Поэтому для построения критического пути необходимо вычислить резерв времени на исполнение работ.

Очевидно, никакая работа _i,j не может начаться ранее наступления события х_i и не должна закончиться позже события х_j. Таким образом, без задержки всего проекта можно выделить на исполнение операции (t_n(х_j)-t_p(х_i)) единиц времени.

Если _i,j⁰=(t_n(х_j)- t_p(х_i)-_i,j) равно нулю, то данная работа (i,j) не имеет резерва времени, т.е. находится на критическом пути. Величину _i,j⁰=(t_n(х_j)- t_p(х_i)-_i,j)0 называют полным резервом времени операции (i,j). На рис. 54 дан пример поиска полного резерва времени для трех операций. Все события для данного примера имеют нулевой резерв времени, но для поиска критического пути необходимо также найти резерв времени по работам. В данном примере резерв времени по работам равен:

_1,2⁰=(4-2-2)=0; _1,3⁰=(8-2-4)=2; _2,3⁰=(8-4-4)=0.

Следовательно, работы (х₁;х₂) и (х₂;х₃) лежат на критическом пути, а работа (х₁;х₃) имеет резерв времени.

Резерв времени является показателем гибкости планирования сроков в сетевой модели. Поэтому кроме критического пути с помощью полного резерва времени на исполнение операций, решают задачи по использованию трудовых, материальных и финансовх ресурсов, по перераспределению работ на определенный период года, месяца или суток. Для этого привлекают знания о свободном, независимом и гарантированном резерве времени.

Интересно отметить, что все эти резервы времени могут быть сведены в таблицу (см. таблицу16), которая показывает взаимосвязь различных показателей резерва времени.

Таблица 16.

	ранний момент события хj tp(xj)	поздний момент события хj tn(xj)
ранний момент события хi tp(xi)	свободный резерв времени работы (хi;хj) i,j0 своб.	полный резерв времени работы (хi;хj) i,j0 полн.
поздний момент события хi tn(xi)	независимый резерв времени работы (хi;хj) i,j0 незав.	гарантированный резерв времени работы (хi;хj) i,j0 гаран.

_i,j^{0 полн.}=(t_n(х_j)- t_p(х_i)-_j,i);

_i,j^{0 своб.}=(t_p(х_j)- t_p(х_i)-_j,i);

_i,j^{0 незав.}=(t_p(х_j)- t_n(х_i)-_j,i);

_i,j^{0 гаран.}=(t_n(х_j)- t_n(х_i)-_j,i).

Для иллюстрации возможностей сетевого планирования и управления рассмотрим сетевую модель (см. рис. 55). Для компактного изображения всех показателей каждого события каждую вершину графа представим в виде круга, разбитого на четыре сектора. В каждом секторе указаны четыре показателя: индекс вершины (i), ранний момент наступления события t_p(x_i), поздний момент наступления события t_n(x_i) и время ожидания события t⁰(i). Дуги графа изображают работы, а пунктирная линия-ожидание.

Для упорядочения расчета раннего и позднего моментов наступления событий необходимо выполнить правильную нумерацию вершин графа.

Алгоритм нумерации вершин графа:

шаг 1: присвоить начальной вершине сетевой модели индекс “0”; принять p=0, где p-шаг итерации;

шаг 2: присвоить на шаге итерации p любой неиндексированный вершине, смежной с индексированными вершинами, индекс (p+1);

шаг 3: если p=(n+1), то конец, при этом индекс (n+1)=k, иначе принять p=(p+1) и перейти к шагу 2 алгоритма.

Следует отметить, что нумерация вершин ациклического графа называется правильной на дуге (х_i;х_j)G, если i<j, и правильной на графе G, если она правильна на всех его дугах.

Алгоритм расчета раннего момента наступления событий.

шаг 1: принять для начальной вершины графа t_p(0)=0, p=0, где p-шаг итерации;

шаг 2: определить на шаге итерации p ранний момент наступления события j по формуле: t_p(j)=(t_p(i)+_j,i), где t_p(i)-события i с известным ранним моментом наступления; _j,i-продолжительность работы (i,j) от события, имеющего t_p(i);

а) если к вершине j подходит одна дуга (i,j), то принять t_p(j)=(t_p(i)+_j,i),

б) если к вершине j подходит несколько дуг {(i,j)}, то сравнить и найти максимальное значение раннего момента наступления события j по формуле: t_p(j)=max_i{t_p(i)+_i,j}.

Таблица 17.

pi	i	j=i	tp(j)={tp(i)+i,j}	tp(j)=maxi{tp(i)+i,j}
0	0	1	tp(1)=tp(0)+0,1=3	tp(1)=3
		2	tp(2)=tp(0)+0,2=2
1	1	2	tp(2)=tp(1)+0,2=8	tp(2)=8
		3	tp(3)=tp(1)+1,3=5	tp(3)=5
		5	tp(5)=tp(1)+1,5=10
2	2	4	tp(4)=tp(2)+2,4=18	tp(4)=tp(5)=18
3	3	5	tp(5)=tp(3)+3,5=13
4	4	6	tp(6)=tp(4)+4,6=20
		7	tp(7)=tp(4)+4,7=22	tp(7)=22
5	5	6	tp(6)=tp(5)+4,6=22	tp(6)=22
		k	tp(k)=tp(5)+5,k=24
6	6	k	tp(k)=tp(6)+6,k=27	tp(k)=27
7	7	k	tp(k)=tp(7)+7,k=23

шаг 3: если p=(n+1), то конец, иначе принять p=(p+1) и перейти к шагу 2 алгоритма.

Результаты вычислений раннего момента наступления событий удобно представить таблицей (см. таблицу 17)

Рис. 55. Сетевая модель.

Алгоритм расчета позднего момента наступления события.

шаг 1: принять для конечной вершины графа t_n(k)=t_p(k); р=0, где р-шаг итерации;

шаг 2: определить на шаге итерации р поздний момент наступления события j по формуле: t_n(j)=(t_n(i)-_j,i), где t_n(i)-событие i с известным поздним моментом наступления; _j,i-продолжительность работы (i,j) от события, имеющего t_n(i);

а) если от вершины j отходит одна дуга (i,j),то принять t_n(j)=(t_n(i)-_j,i);

б) если от вершины j отходит несколько дуг (i,j), то сравнить и найти минимальное значение позднего момента наступления события j по формуле: t_n(j)=min_i{(t_n(i)-_j,i)};

шаг 3: если р=(n+1), то конец, иначе принять р=(р+1) и перейти к шагу 2 алгоритма.

Результаты вычисления позднего момента наступления события удобно представить таблицей (см. таблицу 18).

Таблица 18.

pi	i	j=i-1	tn(j)=(tn(i)-j,i)	tn(j)=mini{(tn(i)-j,i)}
0	k	7	tn(7)=(tn(k)-k,7)=26	tn(7)=26
		6	tn(6)=(tn(k)-k,6)=22	tn(6)=22
		5	tn(5)=(tn(k)-k,5)=21
1	7	4	tn(4)=(tn(7)-4,7)=22	tn(5)=tn(4)=18
2	6	5	tn(5)=(tn(6)-5,6)=18
		4	tn(4)=(tn(6)-4,6)=20
3	5	3	tn(3)=(tn(5)-3,5)=10	tn(3)=10
		1	tn(1)=(tn(5)-1,5)=11
4	4	2	tn(2)=(tn(4)-2,4)=8	tn(2)=8
5	3	1	tn(1)=(tn(3)-1,3)=8
6	2	1	tn(1)=(tn(2)-1,2)=3	tn(1)=3
		0	tn(0)=(tn(2)-0,2)=6
7	1	0	tn(0)=(tn(1)-0,1)=0	tn(0)=0

Алгоритм расчета резерва времени события.

шаг 1: принять р=0, где р-шаг итерации;

шаг 2: определить на шаге итерации р индекс события и резерв его ожидания по формуле: t₀(i)=(t_n(i)-t_p(i));

шаг 3: если р=(n+1), то конец, иначе принять р=(р+1) и перейти к шагу 2.

Результаты вычислений резервов времени для событий удобно представить таблицей (см. таблицу 19).

Таблица 19.

pi	0	1	2	3	4	5	6	7	8
i	0	1	2	3	4	5	6	7	k
t0(i)	0	0	0	5	0	0	0	4	0

Алгоритм расчета резерва времени на работы.

шаг 1: принять р=1 и выделить любую дугу (i,j);

шаг 2: определить резерв времени для работы (i,j) по формулам:

а) полный резерв времени: _i,j^{0 полн.}=(t_n(j)- t_p(i)-_j,i);

б) свободный резерв времени: _i,j^{0 своб.}=(t_p(j)- t_p(i)-_j,i);

в) независимый резерв времени: _i,j^{0 незав.}=(t_p(j)- t_n(i)-_j,i);

г) гарантированный резерв времени: _i,j^{0 гаран.}=(t_n(j)- t_n(i)-_j,i);

шаг 3: если р=m, где m-число дуг сетевой модели, то конец, иначе р=(р+1), выделить новую дугу (i,j) и перейти к шагу 2 алгоритма.

Таблица 20.

(i,j)	i,j0 полн.	i,j0 своб.	i,j0 незав.	i,j0 гарант.	pi
(0,1)	0	0	0	0	1
(0,2)	6	6	6	6	2
(1,2)	0	0	0	0	3
(1,3)	5	0	0	5	4
(1,5)	8	8	8	8	5
(2,4)	0	0	0	0	6
(3,5)	5	5	0	0	7
(4,6)	2	2	2	2	8
(4,7)	4	0	0	4	9
(5,6)	0	0	0	0	10
(5,k)	3	3	3	3	11
(6,k)	0	0	0	0	12
(7,k)	4	4	0	0	13

Результаты расчетов резервов времени для выполнения работ приведены в таблице 20.

Выполненный анализ показывает, что

1) события, за которыми нужно следить с особым вниманием, имеют резерв времени равный нулю; это события 0;1;2;4;5;6;k;

2) работы, которые лимитируют продолжительность всего проекта, имеют полный резерв времени равный нулю; это работы (0;1); (1;2); (2;4); (5;6); (6;k);

3) работы, которые имеют резерв времени (полный, свободный, независимый и гарантированный), позволяют соответственно уменьшить затраты трудовых, финансовых или материальных ресурсов и продлить исполнение этих работ, но не более указанных резервов; это работы (0;2); (1;5); (4;6); (5;k);

4) работы, которые имеют свободный резерв времени равным нулю, определяют необходимость контроля за ранним моментом наступления событий, предшествующих данной работе и влияющих на начало последующих работ; это работы (1;3); (4;7);

5) работы, которые имеют независимый резерв времени равным нулю, определяют необходимость контроля за поздним моментом наступления событий, предшествующих данной работе, и влияющих на развитие последующих работ, что является удобным показателем свободы планирования; это работы (1;3); (3;5); (4;7); (7;k);

6) работы, которые имеют гарантированный резерв времени равным нулю, являются удобным показателем планирования работ проекта, т.к. они не влияют на исполнение всего проекта, но позволяют гарантированно отслеживать исполнение отдельных работ; это работы (3;5); (4;7).

Контрольные вопросы и задачи.

1. Что такое остов графа?

х₂

х₁ х₃

х₅ х₄

2. Чему равно цикломатическое число графа и сколько можно построить покрывающих остовов?

3. Найти остов графа по алгоритму Дейкстра (см. приложение 1).

4. Найти остов графа по алгоритму Краскала (см. приложение 1).

5. Найти кратчайшие пути на графе по алгоритму Флойда (см. приложение 2).

6. Найти распределение максимального потока в сети по алгоритму Форда-Фалкерсона (см. приложение 3).

7. Найти критический путь по алгоритму управления проектом (СПУ) (см. приложение 4).

8. Определить числа графа (см. приложение 5).

118