
Глава 3. Основы теории графов.
3.1. Граф и его характеристики.
Совокупностью объектов произвольной природы и отношений между каждой парой этих объектов может быть изображено на плоскости в виде множества точек, являющихся образом множества объектов, и множества отрезков линий, соединяющих пары точек, что является образом множества отношений. Такой образ совокупности объектов и отношений принято называть графом. Множество точек, являющихся образом множества объектов, называют вершинами графа, а множество отрезков линий, являющихся образом множества отношений, - рёбрами или дугами графа.
Вершинами графа могут быть узлы любой транспортной или электрической сети, операторы программы или команды операционной системы, события в любой сфере человеческой деятельности, а рёбрами или дугами - линии связи в транспортной или в электрической сети, в организации работы на компьютере или в любой сфере человеческой деятельности.
Граф может быть задан в двух формах:
а) G=<X;r>,
где r={(xi;xj)|xi,xj X}(XX) или
б) G=<X;h>,
где h={{xj}Xi|xi,xj X}(XX) (см. 1.2).
Обе формы представления графа имеют широкое распространение. Первая форма применяется в тех случаях, когда необходимо отмечать дополнительные характеристики об отрезках линий: протяжённость, загрузка, пропускная способность и т.п.
Вторая форма применяется в тех случаях, когда необходимо фиксировать дополнительные характеристики о вершинах графа: время исполнения команды или оператора, надёжность или загруженность узла транспортной или электрической сети. Вторая форма наиболее экономна в использовании памяти компьютера и хорошо реализуется списочными структурами данных.
Граф G=<X;r> называют неориентированным, если (xi;xj)=(xj;xi), в этом случае отрезок линии (xi;xj) называют ребром.
Граф G=<X;r> называют ориентированным, если (xi;xj)(xj;xi), в этом случае отрезок линии (xi;xj) называют дугой.
На рис. 16 приведены неориентированный и ориентированный графы.
Любая программа или электронная схема, любой производственный или вычислительный процесс могут быть представленны ориентированным графом, а любая схема транспортной или электрической сети - неориентированным графом.
Граф G=<X;r>, между двумя вершинами которого может быть задано несколько рёбер или дуг, называют мультиграфом.
Для определения отношения принадлежности вершин графа ребру или дуге и, наоборот,рёбер или дуг-вершине вводится понятие “инциденции”, т.е. вершина xi инцидентна ребру или дуге (xi;xj), если она является концевой вершиной данного отрезка линии, а ребро или дуга (xi;xj) инцидентна вершине xi , если отрезок линии ограничен концевой вершиной xi . Следует обратить внимание, что отношение принадлежности, определяющее понятие “инциденции”, устанавливает связь между элементами двух разных множеств X и r.
Число вершин, инцидентных ребру или дуге, всегда равно 2, т.к. они являются концевыми вершинами отрезка линии.
Число рёбер или дуг, инцидентных вершине xi, может быть произвольным. Его называют степенью или валентностью вершины xi и обозначают i=j(xi;xj).
Число дуг для ориентированного графа G=<X;r>, исходящих из вершины xi, называют полустепенью вершины графа и обозначают i+=j(xi;xj)+. Вершину xi, инцидентную исходящей дуге (xi;xj)+, называют вершиной - истоком.
а
r0,1
r1,5
r3,5
r0,1
r1,5
r3,5
r1,4
r1,4
x0
x5
x0
x5
r0,4
r4,5
r0,4
r4,5
x2
x2
r4,4
r4,4
Рис.16. Неориентированный
(а) и ориентированный (б) графы.























 )
x1
r1,3
x3
б) x1
r1,3
x3
)
x1
r1,3
x3
б) x1
r1,3
x3



 x4
x4
x4
x4
Две вершины графа называются смежными, если они различны и между ними существует ребро или дуга.
Вершина xi, несмежная ни с одной вершиной графа, называется изолированной. На рис.16 изолированной является вершина x2 .
Два ребра также называются смежными, если они различны и имеют общую вершину.
Последовательность смежных рёбер или дуг, соединяющих вершины xi и xj , называют маршрутом и обозначают i,j=((xi,xk);…. . . (xl;xj)). Например, для графа на рис.16а) между вершинами x0 и x5 существует шесть маршрутов, т.е.
0;5={(r0;4;r4;5);(r0;1;r1;4;r4;5);(r0;1;r1;5);(r0;4;r4;1;r1;5);(r0;4;r4;1;r1;3;r3;5); (r0;1;r1;3;r3;5)}.
Последовательность смежных вершин маршрута, соединяющего вершину xi и xj , называют переходом и обозначают i,j=(xi;…. . .xj). Например, для графа на рис.16а) между вершинами x0 и x5 существует шесть переходов, т.е.
0;5={(x0;x4;x5);(x0;x1;x4;x5);(x0;x1;x5);(x0;x4;x1;x5);(x0;x4;x1;x3;x5);(x0;x1;x3;x5).
Маршрут неориентированного графа G=<X;r>, связывающий вершины xi и xj , называют цепью.
Маршрут ориентированного графа G=<X;r>, связывающий вершины xi и xj , называют путём.
Маршрут называют простым, если при его обходе каждая промежуточная вершина встречается не более одного раза.
Маршрут называют открытым, если его концевые вершины различны, и замкнутым, если его концевые вершины совпадают.
Замкнутый маршрут для неориентированного графа называют циклом, а для ориентированного графа - контуром.
Маршрут называют эйлеровым, если он замкнут и проходит через каждое ребро графа только по одному разу.
Маршрут называют гамильтоновым, если он замкнут и проходит через каждую вершину графа только по одному разу.
Длина маршрута равна числу смежных рёбер, соединяющих вершины xi и xj , т.е. li;j=rk,l, где kl и ik,lj.
Длину минимального маршрута, соединяющего вершины xi и xj называют расстоянием. Так расстояние между вершинами x0 и x5 графа, приведённого на рис.16а), равно 2.
Замкнутый маршрут, который содержит только одно ребро или дугу (длина маршрута равна 1), называют петлёй. На рис.16 петля указана для вершины x4.
Если ребро или дуга обладают дополнительной характеристикой - протяжённостью lk,l, то длина маршрута равна сумме длин рёбер или дуг, его составляющих, т.е. li;j=k,l, где kl и ik,lj.
Если ребро или дуга обладают дополнительной характеристикой - пропускной способностью, то пропускная способность маршрута равна минимальной пропускной способности для множества рёбер или дуг, его составляющих.
Граф G=<X;r> называют связным, если любые две его вершины можно соединить цепью. Для ориентированного графа выделяют сильную связность, когда любые две его вершины взаимодостижимы при наличии дуг, и слабую связность, когда любые две его вершины достижимы только при условии замены дуг на рёбра.
Граф G=<X;r> называют полным, если любые две его вершины смежны между собой (см. рис.17а)).
Граф G=<X;r> называют пустым, если любые две его вершины не смежны между собой (см. рис.17б)).
Граф G=<X;r> называют дополнительным для графа G=<X;r>, если он опирается на множество вершин графа G, которые смежны для графа G только в случае их несмежности в графе G, т.е. r=r. Так пустой граф (см. рис.17б)) есть дополнительный для полного графа (см. рис.17а)).
Граф G=<X;r> называют деревом, если он связный, но без циклов, петель и кратных рёбер или дуг (см. рис.18а)).
Граф G=<X;r> называют лесом, если он несвязный и без циклов, петель и кратных рёбер или дуг (см. рис.18б)).
Расстояние от вершины xi для графа типа дерево до наиболее удалённой вершины xj называют эксцентриситетом графа и обозначают i.
Множество вершин графа типа дерево, имеющих минимальный эксцентриситет, формируют центроид графа. Наибольшее значение эксцентриситета для множества вершин графа типа дерево определяет диаметр графа. Одна из вершин центроида по выбору формирует центр графа. На рис. 18 представлены основные характеристики графа типа дерево.
Следует обратить внимание, что в связном графе типа дерево число рёбер всегда равно (n-1), где n - число вершин графа.
x1
x1
x
x4
x3
x4
x3
Рис. 17. Полный (а) и пустой (б) графы.



 а)
б)
а)
б)







 3
x2
x5
x2
3
x2
x5
x2




а
центр
1
5 5 2
2
Рис. 18. Граф типа дерево (а) и лес (б).
 )
диаметр
б)
)
диаметр
б)






 6 эксцентриситет 7
3 3
6 эксцентриситет 7
3 3




 5 центроид 6
2 2
5 центроид 6
2 2















 6 4 5 2
2 2
6 4 5 2
2 2







 7
4 6 3
3
7
4 6 3
3



Если множество вершин графа G=<X;r> разбить на два подмножества X и X\X при условии, что X(X\X)=X и X(X\X)=, то множество рёбер графа, одни из концевых вершин которых принадлежат множеству X, а другие - множеству (X\X), называют разрезом графа. Поиск разрезов сводится к определению отношения принадлежности xiX и xj(X\X) с последующим определениям множества рёбер, соединяющих X` и (X\X). На рис. 19 дан разрез графа, представленного на рис. 16а), для двух несмежных вершин x0 и x5 и одного из возможных разбиений множества вершин графа на два подмножества X={x0;x1;x2} и (X\X)={x3;x4;x5}.















x1
x3
x0
X
X\X
x5
x2
r0,4
x4
Рис. 19. Разрез графа.

 r1,3
r1,3
 r1,5
r1,5 r1,4
r1,4
Наименьшее число рёбер, удаление которых превращает связный граф в несвязный, называется числом рёберной связности.
Наименьшее число вершин, удаление которых превращает связный граф в несвязный, называют числом вершинной связности.
Одна вершина, удаление которой превращает связный граф в несвязный, называется точкой сочленения, а одно ребро, удаление которого также превращает связный граф в несвязный, - мостом. На рис. 20 представлены точка и мост сочленения связного графа.
а) удаление точки
сочленения x3
x1 x4
x1
x4
x0 x3
x6
x0
x6
x2 x5
x2
x5
б) удаление моста сочленения (x3;
x4)
x1
x5
x1 x5
x2
x6
x2 x6
Рис. 20. Точка(а) и мост(б) сочленения
связанного графа.





 точка
точка



































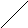 мост
мост









 x0
x3
x4 x7
x0 x3
x4
x
x0
x3
x4 x7
x0 x3
x4
x
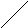
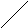



 7
7



Граф G=<X;r> называют двудольным или бихроматическим, если множество его вершин можно разбить на два подмножества X и (X\X) при условии, что X(X\X)=X и X(X\X)=. Двудольные графы удобны для исследования попарно несмежных рёбер, т.е. поиска паросочетаний, а также для задания бинарных отношений между элементами различных множеств.
Граф G=<X;r> называют частичным для графа G=<X;r>, если он порождён подмножеством рёбер или дуг исходного графа, т.е. rr вместе с концевыми вершинами этих рёбер, т.е. XX. Например, для графа,приведённого на рис. 16а), задание подмножества рёбер r={r0;1;r0;4;r1;5;r4;5} формирует частичный граф G=<X;r>(см. рис. 21а)).
Граф G=<X;r> называют суграфом графа G=<X;r>, если он также порождён подмножеством рёбер или дуг исходного графа, т.е. rr, но использует все вершины исходного графа, т.е. X=X. Например, для графа, приведённого на рис. 16а), задание подмножества рёбер r={r0;1;r0;4;r1;5;r4;5} формирует частичный суграф G=<X;r>(см. рис. 21б)).
Граф G=<X;r> называют подграфом графа G=<X;r>, если он порождён подмножеством вершин исходного графа, т.е. XX, вместе с рёбрами или дугами, обе концевые вершины принадлежат множеству X. Например, для графа, приведённого на рис. 16а), задание подмножества вершин X={x0;x1;x3;x4;x5} формирует подграф G=<X;r>(см. рис. 21в)).
Суграф G=<X`;r`> связанного графа G=<X;r>, формируемый в виде дерева, т.е. без циклов, петель и кратных рёбер, называют остовом графа G=<X;r>. Например, для связанного подграфа, представленного на рис. 21в), остовом является суграф, представленный на рис. 21г).
а) x1
б)
x1
x3
r0,1
r1,5
r0,1
r1,5
x0
x0
x4
x2
x4
в) x1
r1,3 x3
г)
x1
r1
r3,5
r0,1
r1,5
r0,1
r1,5
x0 r0,4
r4,5
r0,4
x4
r4,4
Рис. 21. Частичный граф,
суграф, подграф и остов графа G=<X;r>.
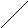



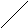









 x5
x5
x5
x5 r0,4
r4,5
r0,4
r4,5
r0,4
r4,5
r0,4
r4,5




 ,3
x3
,3
x3
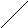

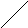






 x5
x5


 x0
x5
x0
x5
 x4
x4
Граф G=<X;r> называют плоским или планарным, если он может быть изображён на плоскости так, что вершинам соответствуют различные точки плоскости, а линии, соответствующие рёбрам и дугам графа, не пересекаются. Плоские графы используют при анализе и проектировании печатных плат, сетей коммуникации и т.п. На рис. рис. 16, 18, 20 приведены плоские графы, а на рис. 17а)-неплоский.
Граф G=<X;r> называют взвешенным, если его рёбра или вершины имеют дополнительные характеристики: продолжительность во времени или протяжённость в пространстве, нагрузку или надёжность функционирования. Так время исполнения команды операционной системы или оператора программы, вероятность наступления события или надёжность эксплуатации узла и т.п. определяют вес вершины графа, а протяжённость линий транспортных или электрических сетей, их пропускная способность по какому-либо параметру определяют вес ребра или дуги. На рис. 22 приведён взвешенный граф, дуги и вершины которого имеют условные веса. Взвешенные графы чаще называют сетями.
(p1=0,4)
x1
r1,3=2
x3
(p3=0,8)
r0,1=2
r3,5=3
(p0=0,6)
x5
(p5=0,9)
x4
Рис. 22. Взвешенный граф.








 x0
r1,4=4
r1,5=5
x0
r1,4=4
r1,5=5


 r0,4=5
r4,5=3
r0,4=5
r4,5=3
а)
ri,j
(xi;xj)
r0,1
(x0;x1)
r0,4
(x0;x4)
r1,3
(x1;x3)
r1,4
(x1;x4)
r1,5
(x1;x5)
r3,5
(x3;x5)
r4,4
(x4;x4)
r4,5
(x4;x5)
г)
xi
Pi
x0 0,6
x1 0,4
x3 0,8
x4 0,6
x5 0,9
в)
xi
hXi={…}
x0
x1;x4
x1
x3;x4;x5
x3
x5
x4
x5
x5 0
|
|
б) |
|
ri,j |
li,j |
|
r0,1 |
2 |
|
r0,4 |
5 |
|
r1,3 |
2 |
|
r1,4 |
4 |
|
r1,5 |
5 |
|
r3,5 |
3 |
|
r4,4 |
0 |
|
r4,5 |
3 |
Рис. 23. Формы представления графа.
На рис. 23а) указана форма для представления инциденции дуг и вершин графа. В левом столбце приведены индексированные дуги графа, а в правом-вершины графа, им инцидентные. На рис. 23б) дана форма для рёберно-взвешенного графа. Чаще всего эти две таблицы объединяют.
На рис. 23в) указана форма для представления смежности вершин графа. В левом столбце приведены индексированные вершины графа, а в правом-вершины, смежные им. На рис. 23г) дана форма для вершинно-взвешенного графа. Чаще всего эти две таблицы объединяют.
Представление графа таблицами отношений G=<X;r>наиболее удобно для хранения и обработки информации о весе ребра или дуги и ускоренного поиска инцидентных им вершин, а представление графов таблицами отображений G=<X;h> наиболее удобно для хранения и обработки информации о весе вершины и ускоренного поиска смежных вершин.
Матричное описание графа удобно для вычисления различных чисел графа и выполнения различных алгебраических операций, т.к. опирается на глубоко разработанную теорию матриц.
Матрица инциденции. Поскольку инциденция есть отношение принадлежности элемента одного множества X другому множеству r, то матрица инциденции ||hi;j|| есть прямоугольная, число строк которой равно мощности множества |r|=m, а число столбцов - мощности множества |X|=n. Элементы матрицы инциденции для неориентированного графа определяются соотношением:
{
1, если ребро ri;j инцидентно вершинам xi и xj;
hi;j X=
0, в противном случае;
Таблица 9. hX
x0
x1
x2
x3
x4
x5
1 1 0 0 0 0
r0,4 1 0 0 0 1 0
r1,3 0 1 0 1 0 0
r1,4 0 1 0 0 1 0
r1,5 0 1 0 0 0 1
r3,5 0 0 0 1 0 1
r4,4 0 0 0 0 1 0
0 0 0 0 1 1
i 2 4 0 2 4 3



 r0,1
r0,1

 r4,5
r4,5
Элементы матрицы инциденции для ориентированного графа определяются другим соотношением:
{
+1, если дуга ri,j исходит из вершины xi;
hi;j= 0, если дуга ri,j не инцидентна вершинам xi и xj;
-1, если дуга ri,j заходит в вершину xj.
Таблица 10.
h
x0
x1
x2
x3
x4
x5
+1 -1 0 0 0 0
r0,4 +1 0 0 0 -1 0
r1,3 0 +1 0 -1 0 0
r1,4 0 +1 0 0 -1 0
r1,5 0 +1 0 0 0 -1
r3,5 0 0 0 +1 0 -1
r4,4 0 0 0 0 +1 0
0 0 0 0 +1 -1
i+ 2 3 0 1 2 0
i- 0 1 0 1 3 3



 r0,1
r0,1

 r4,5
r4,5
В каждом столбце матрицы инциденции число “+1” равно полустепени исхода вершины xi, т.е. i+, а число “-1” равно полустепени захода вершины xi , т.е. i-. Для последующего анализа графа также желательно выделить строки, раскрывающие полустепени всех вершин графа.
Матрицы инциденции в таблицах 9 и 10 выделены прямоугольными скобками [ ].
Матрица смежности. Поскольку смежность есть бинарное отношение между элементами одного множества, то матрица смежности ||ri,j|| есть квадратная матрица, число строк и столбцов которой равно мощности множества |X|=n.
Элементы матрицы смежности определяются соотношением:
{
1, если вершина xi смежна вершине xj;
ri,j=
0, в противном случае.
В таблице 11 представлена матрица смежности для неориентированного графа (см. рис. 16а)). Элементы матрицы смежности, равные 1, расположены симметрично относительно главной диагонали. В каждой строке и в каждом столбце такой матрицы число “1” равно степени вершины, т.е. i. Поэтому можно выделить дополнительную строку или столбец для хранения информации о степени каждой вершины графа.
Таблица 11. r
x0
x1
x2
x3
x4
x5
i
0 1 0 0 1 0 2
x1 1 0 0 1 1 1 4
x2 0 0 0 0 0 0 0
x3 0 1 0 0 0 1 2
x4 1 1 0 0 1 1 4
0 1 0 1 1 0 3
i 2 4 0 2 4 3
Таблица 12.
r0
x0
x1
x2
x3
x4
x5
i+
0 1 0 0 1 0 2
x1 0 0 0 1 1 1 3
x2 0 0 0 0 0 0 0
x3 0 0 0 0 0 1 1
x4 0 0 0 0 1 1 2
0 0 0 0 0 0 0
i- 0 1 0 1 3 3



 x0
x0

 x5
x5



 x0
x0

 x5
x5
В таблице 12 представлена матрица смежности для ориентированного графа (см. рис. 16б)), но при условии, что строки заданы вершинами-истоками графа, а столбцы - вершинами-стоками. Поэтому итоговый столбец таблицы- i+ показывает полустепень каждой вершины-истока, а итоговая строка- I- - полустепень каждой вершины-стока.
По структуре матрицы смежности можно сделать выводы:
-
каждый ненулевой элемент главной диагонали соответствует петле на графе;
-
матрица смежности для неориентированного графа симметрична относительно главной диагонали;
-
матрица смежности для ориентированного графа несимметрична относительно главной диагонали;
-
если в графе необходимо добавить вершину, несмежную с остальными вершинами, то к матрице смежности следует добавить столбец и строку, элементы которой содержат только “0”;
-
столбец ориентированного графа, все элементы которого имеют значение “0”, соответствует вершине-истоку всего графа;
-
строка ориентированного графа, все элементы которой имеют значение “0”, соответствует вершине-стоку всего графа.
Матрица весов. Протяжённость ребра или дуги, а также затраты времени, энергии или финансов на перемещение пакета информации или транспортной единицы по ребру или дуге из вершины xi в вершину xj формирует рёберно-взвешенный граф.
Элементы матрицы весов рёберно-взвешенного графа определяются соотношением:
{
ri,j=
li,j, если вершина xi смежна вершине xj и вес ребра li,j;
, если вершина xi несмежна вершине xj.
Таблица 13.
rВ
x0
x1
x2
x3
x4
x5
0
2
5
x1
2
0
2
4
5
x2
x3
2
0
3
x4
5
4
0
3
x5
5
3
3
0



 x0
x0


Контрольные вопросы и задачи.
1. Граф задан таблицей отношений:
|
rk |
r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
r7 |
|
(xi;xj) |
(x1;x2) |
(x1;x3) |
(x2;x5) |
(x3;x4) |
(x2;x4) |
(x4;x6) |
(x5;x6) |
-
нарисуйте граф;
-
определите степени вершин графа;
-
укажите маршрут и переход из вершины x3 в вершину x6;
-
сколько всего маршрутов между вершинами x1 и x6;
-
найдите дополнительный граф;
-
укажите разрез для X={x1;x2;x4} и X\X={x3;x5;x6};
-
какой подграф будет получен после удаления вершины x2;
-
нарисуйте частичный граф на рёбрах {r2;r4;r6};
-
нарисуйте суграф на рёбрах {r1;r3;r5;r7};
-
нарисуйте подграф на вершинах x2,x4,x5,x6;
-
определите является ли плоским данный граф;
-
нарисуйте матрицу инциденции графа;
-
нарисуйте матрицу смежности графа.
2.Граф задан таблицей отображений :
|
xi |
x |
x |
x |
x |
x |
x |
x |
x |
x |
|
hXi |
x2 |
x1 , x4 |
x4 |
x2,x3,x5,x6 |
x4 , x7 |
x4 |
x5,x8,x9 |
x7 |
x7 |
-
нарисуйте граф;
-
определите эксцентриситет каждой вершины графа;
-
найдите центр графа;
-
найдите диаметр графа;
-
определите степени вершин графа;
-
найдите дополнительный граф;
-
какие будут подграфы после удаления каждой вершины графа;
-
нарисуйте матрицу инциденции графа;
-
нарисуйте матрицу смежности графа.
-
Числовые характеристики графа.
Функции, заданные на множестве графов {G=<X;r>} и принимающие значения на множестве целых чисел, называют числовыми характеристиками графа или просто числами графа.
Наиболее очевидными и простыми числами графа являются: число вершин графа - n, число рёбер или дуг графа - m, степени и полустепени вершин графа - i(или i+/i-).
Все остальные характеристики графа требуют поиска и вычисления их значений.
{
Xi=X;
XiXj=, для ij, 1 i,j n;
Gi=G;
GiGj=, для ij, 1i,jn;
x10
x9
x11
Рис. 24. Компоненты связности графа
G=<X;r>.

 G
x2
x6
G
x2
x6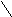



 G1
G2
G1
G2






 x1
x3
x5
x7
x1
x3
x5
x7

 x4
x8
x4
x8

 G3
G3
Для поиска числа компонент связности графа используют механизм вычисления матрицы достижимости и определения полных подграфов. Подробнее см. 3.3.
На рис. 24 в качестве примера дан трёхкомпонентный граф:
G=<X;r>, где X={x1;x2;x3;x4;x5;x6;x7;x8;x9;x10;x11},
G1=<X1;r1>, где X1={x1;x2;x3;x4},
G2=<X2;r2>, где X2={x5;x6;x7;x8},
G3=<X3;r3>, где X3={x9;x10;x11},
X1X2X3=X; X1X2=; X1X3=; X2X3=; G1G2G3=G.
Цикломатическое число графа G=<X;r>. Наименьшее число рёбер, удаление которых приводит к графу без циклов и петель, называют цикломатическим числом и обозначают (G). Цикломатическое число можно определить по формуле:
(G)=m-n+æ(G),
где m - число рёбер, n - число вершин, æ(G) - число компонент связности графа.
G
x2
x3
x1
x4
x7
x6
x8
Рис. 25. Цикломатическое
число графа G=<X;r>.















 x5
x5

n=8, m=10, æ(G)=2.
Следовательно, (G)=10-8+2=4. Можно убрать рёбра
{(x1;x2),(x2;x3),(x2;x4),(x6;x8)} или {(x1;x5);(x4;x5);(x3;x4);(x6;x7)}. Выбор устраняемых рёбер для ликвидации циклов определяется другой задачей.
Хроматическое число графа G=<X;r>. Раскраской вершин графа в цвета называют разбиение множества вершин графа на попарно непересекающиеся непустые подмножества, состоящие из попарно несмежных вершин, т.е.
X=X1X2…X;
XiXj=, где i j, 1i,j.
Тогда каждому подмножеству Xi можно соотнести особый цвет краски. В этом случае никакие две смежные вершины не могут быть окрашены в один цвет. Наименьшее число , при котором никакие две смежные вершины графа не могут быть окрашены в один цвет, называют хроматическим числом графа.
Нахождение хроматического числа достаточно трудоёмкая задача, имеющая сложный алгоритм и требующая большого объёма вычислений. Однако, можно дать оценку этого числа. Так хроматическое число полного n-вершинного графа равно n, пустого графа - 1, графа с циклом чётной длины - 2, графа с циклом нечётной длины - 3, графа типа дерево - 2. В отдельных случаях может быть рекомендована оценка по следующей формуле: maxi{i+1}.
Например, для графа, приведённого на рис. 25, хроматическое число равно 3, т.к. он содержит циклы нечётной длины: пусть x1 - красный, x2 - синий, x3 - зелёный, x4 - красный, x5 - зелёный, x6 - красный, x7 - синий, x8 - зелёный.
Плотность графа G=<X;r>. Наибольшее число вершин полного подграфа G=<X;r>, между всеми вершинами которого задано отношение смежности, называют плотностью графа G и обозначают (G), т.е.
(G)= maxi{|Xi|}.
Например, для графа, приведённого на рис. 24, плотность графа равна 3, а на рис. 17а) - 5. Подробнее см. 3.3.
Неплотность графа G=<X;r>. Наибольшее число вершин пустого подграфа G=<X;r>, между всеми вершинами которого отсутствует отношение смежности, называют неплотностью графа G и обозначают (G), т.е.:
(G)= maxi{|Xi|}.
Очевидно, что(G)=(G) и (G)=(G). Для графа,приведённого на рис. 17б) неплотность графа равна 5.
Число внутренней устойчивости графа G=<X;r>. Наибольшее число попарно несмежных вершин графа G формирует число внутренней устойчивости графа.
Для поиска этого числа следует воспользоваться условием:
hxiS=, где xiS, SX и S-множество несмежных вершин графа G.
Таких подмножеств в графе G может быть несколько. Выбор из множества {S} подмножества с наибольшим числом вершин определяет число внутренней устойчивости, т.е.
(G)=maxi{|Si|}.
Подробнее о поиске числа внутренней устойчивости см. 3.3.
Число внешней устойчивости графа G=<X;r>. Наименьшее число вершин графа G смежных со всеми остальными вершинами графа формирует число внешней устойчивости графа. Для поиска этого числа следует воспользоваться условием:
hxiТxiT, TX и T-множество вершин графа G, смежных c вершинами X\T.
Таких подмножеств в графе G может быть несколько. Выбор из множества {T} подмножества с наименьшим числом вершин определяет число внешней устойчивости, т.е.
(G)=mini{|Ti|}.
Подробнее о поиске числа внешней устойчивости см. 3.3.
Контрольные вопросы и задачи.
-
Найти число компонент связности для графа








 1 2 3 4 5
1 2 3 4 5
|
|
|
|
|
-
6 7 8 9 10
-
Найти цикломатическое число для графа
5
6 7
8

 1 2
3
1 2
3








 4
4




3. Указать хроматическое число для графа
-
-
x1 x3
-

 x0
x5
x0
x5
-

 x2
x4
x2
x4
Найти число внешней устойчивости для графа (см.п.1). -
-
Найти число внутренней устойчивости для графа (см.п.2).
3.3. Операции над графами.
Алгебраические операции можно выполнять над одним или несколькими графами. Операции над одним графом - унарные операции,- позволяют искать дополнение графа, выполнять слияние (конденсацию) вершин графа, удаление вершин или рёбер графа, поиск основных чисел графа (связности, плотности, устойчивости и т.п.). Операции над двумя графами - бинарные операции,- позволяют выполнять операции объединения, пересечения, композиции, разности, произведения, поиска эквиваленции двух или нескольких графов.
3.3.1. Унарные операции.
{
1, если ri,j=0;
r`i,j =
0, если ri,j=1.
Поэтому, используя матрицу смежности графа G, следует сформировать матрицу смежности для графа G по указанному правилу. На рис. 26а) дан граф G, а на рис. 26б) его дополнение G`.
а) x1
б)
x1
x5
x2
x5
x2
x4
x3
x4
x3

















|
r |
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
0 |
1 |
1 |
1 |
1 |
|
x2 |
1 |
0 |
1 |
0 |
0 |
|
x3 |
1 |
1 |
0 |
1 |
0 |
|
x4 |
1 |
0 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
0 |
|
i |
4 |
2 |
2 |
2 |
1 |
|
r |
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
0 |
0 |
0 |
0 |
0 |
|
x2 |
0 |
0 |
0 |
1 |
1 |
|
x3 |
0 |
0 |
0 |
0 |
1 |
|
x4 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
|
i |
0 |
2 |
1 |
2 |
3 |
Рис. 26. Дополнение графа.
Слияние (конденсация) вершин графа G=<X;r>. При анализе сложных графов возможно полные подграфы заменить фиктивной вершиной, что существенно упрощает весь процесс анализа. Поэтому прежде вcего необходимо найти полные подграфы для данного графа. Для поиска полных подграфов удобно воспользоваться матрицей достижимости, определяющей связность любых вершин графа.
Поскольку hxi={xj} - множество вершин графа, которые достижимы из xi за один “шаг”, то отображение h(h(xi))=hxi2 есть множество вершин достижимых из xi за два “шага”. Так как любая вершина связанного графа должна быть достижима за pn “шагов”, то множество вершин достижимых из вершины xi может быть представлено в виде:
qi+=xi hxihxi2… hxip=j=0phxij.
Для построения матрицы достижимости ||qi,j+|| удобно воспользоваться матрицей смежности ||ri,j||, т.е.
||qi,j+||=||ri.j|| ||ri,j2 ||||ri,j3||…||ri,jn ||=p=1 n||ri,jp||.
Для возведения в степень матрицы смежности следует использовать правила композиции двух отношений (см. 1.7):
ri,j2=k=1n (ri,k rk,j);
ri,j3=k=1n (ri,k rk,j2); и так далее.
На рис. 27 показан процесс построения матрицы достижимости.
Так как в графе есть ориентированные отрезки линий (дуги), то необходимо найти сильную связность. Для этого необходимо прежде всего построить матрицу обратной достижимости, т.е.
||qi,j-1||=||ri,j-1 || ||ri,j-2 ||||ri,j-3|| …||ri,j-n ||=p=1n||ri,j-p||,
и найти пересечение матриц прямой и обратной достижимости. На рис. 28 показан процесс построения матрицы обратной достижимости ||qi,j-1||.
x3
x5
r3
x1
x2
x3
x4
x5
x6
0 1 1 1 1 1
x2 0
1 1 1
1
1
x3 0 1 1 1 1
0
x4 0 1 1 1 1 1
x5 0 0 0 0 0 0
0 0 0 0 0 0



 x2
x4
x2
x4




 x1
x6
x1
x6





 x1
x1

 x6
x6
r2
x1
x2
x3
x4
x5
x6
0 0 1 1 0 0
x2 0
1 1 1
1
1
x3 0 1 1 1 0
1
x4 0 1 1 1 1 0
x5 0 0 0 0 0 0
0 0 0 0 0 0



 x1
x1

 x6
x6
|
r |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
x2 |
0 |
0 |
1 |
1 |
0 |
0 |
|
x3 |
0 |
1 |
0 |
1 |
1 |
0 |
|
x4 |
0 |
1 |
1 |
0 |
0 |
1 |
|
x5 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
q+
x1
x2
x3
x4
x5
x6
1 1 1 1 1 1
x2 0
1 1 1
1
1
x3 0 1 1 1 1
1
x4 0 1 1 1 1 1
x5 0 0 0 0 1 1
0 0 0 0 0 1



 x1
x1

 x6
x6
Рис. 27. Построение матрицы достижимости.
r-2
x1
x2
x3
x4
x5
x6
0 0 0 0 0 0
x2 0
1 1 1
0
0
x3 1 1 1 1 0
0
x4 1 1 1 1 0 0
x5 0 1 1 0 0 0
0 1 0 1 0 0
r-1
x1
x2
x3
x4
x5
x6
0 0 0 0 0 0
x2 1
0 1 1
0 0
x3 0 1 0 1 0
0
x4 0 1 1 0 0 0
x5 0 0 0 1 0 0
0 0 1 0 1 0



 x1
x1

 x6
x6



 x1
x1

 x6
x6
q-
x1
x2
x3
x4
x5
x6
1 0 0 0 0 0
x2 1
1 1 1
0 0
x3 1 1 1 1 0
0
x4 1 1 1 1 0 0
x5 1 1 1 1 1 0
1 1 1 1 1 1



 x1
x1

 x6
x6
|
r-3 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
x2 |
1 |
1 |
1 |
1 |
0 |
0 |
|
x3 |
1 |
1 |
1 |
1 |
0 |
0 |
|
x4 |
1 |
1 |
1 |
1 |
0 |
0 |
|
x5 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
Рис. 28. Построение матрицы контрдостижимости.
q+q-
x1
x2
x3
x4
x5
x6
1 0
0
0 0 0
x2 0
1 1 1
0
0
x3 0 1 1 1 0
0
x4 0 1 1 1 0
0
x5 0 0 0 0
1 0
0 0 0 0 0
1
x1
x
x5
x6




 x1
x1

 x6
x6







Рис. 29. Поиск ||qij+||||qij-||.
Поиск числа компонент связности графа G=<X;r>. Пусть дан неориентированный граф, что может быть образом печатной платы (см. рис. 30). Зрительно данный граф не является планарным и требует формирования многослойной печатной платы. Для решения задачи поиска числа компонент связности графа следует также воспользоваться матрицей достижимости, т.е.
qi,j+=p=1n ri,jp.
Для этого следует задать матрицу смежности исходного графа (см. рис. 30б)) и возводить её в степень до тех пор пока в ней не будет изменений. Для данного графа достаточно вычислить ||ri,j2 ||, т.к. ||ri,j3 ||, ||ri,j4 ||… не дают каких-либо изменений. На рис. 30в) приведена матрица ||ri,j2 || , а на рис. 30г) - матрица достижимости ||qi,j+||=(||ri,j|| ||ri,j2||. Анализ этой матрицы показывает, что некоторые вершины взаимодостижимы не более, чем за два шага, а некоторые недостижимы за любое количество шагов. Если выполнить перестановку строк и столбцов матрицы для соответствующих вершин, то, не изменяя сути достижимости, можно сформировать два блока единичных подматриц (см. рис. 30д)) для двух связанных подграфов. Первый блок опирается на вершины графа X1={x1;x4;x5;x6}, а второй - на вершины графа X2={x2;x3;x7;x8}. Эти два блока формируют два подграфа G1=<X1;r1> и G2=<X2;r2>, не связанных между собой. То есть для исходного графа G=<X;r> число компонент связности равно æ(G)=2.
При анализе ориентированного графа необходимо найти матрицы достижимости и контрдостижимости, определить сильную связность и, выполнив операции перестановки строк и столбцов для соответствующих вершин графа, найти число полных и независимых единичных подматриц. Число этих блоков определит число компонент связности для ориентированного графа.
По этому же алгоритму выполняют поиск плотности графа (G) и, после определения дополнительного графа G, поиск неплотности графа (G)=(G).
а) x1
x2
x3
x4
x5
x6
x7
x8

















|
б) |
|||||||||
|
r |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
x2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
x3 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
x4 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
x5 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
x6 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
x7 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
в) |
||||||||
|
r2 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
|
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
x2 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
x3 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
x4 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
x5 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
x6 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
x7 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
г)
q+ x1 x2 x3 x4 x5 x6 x7 x8
1 0 0 1 1 1 0 0
x2 0 1 1 0 0 0 1 1
x3 0 1 1 0 0 0 1 1
x4 1 0 0 1 1 1 0 0
x5 1 0 0 1 1 1 0 0
x6 1 0 0 1 1 1 0 0
x7 0 1 1 0 0 0 1 1
0 1 1 0 0 0 1 1
д) q+ x1 x4 x5 x6 x2 x3 x7 x8
1 1 1 1 0 0 0 0
x4 1 1 1 1 0 0 0 0
x5 1 1 1 1 0 0 0 0
x6 1 1 1 1 0 0 0 0
x2 0 0 0 0 1 1 1 1
x3 0 0 0 0 1 1 1 1
x7 0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1



 x1
x1

 x8
x8



 x1
x1

 x8
x8
Рис. 30. Поиск числа компонент связности графа.
б) h x1 x2 x3 x4 x5 x6 x7 x8
1 0 0 0 1 0 0 0
r1,6 1 0 0 0 0 1 0 0
r2,3 0 1 1 0 0 0 0 0
r2,7 0 1 0 0 0 0 1 0
r3,7 0 0 1 0 0 0 1 0
r3,8 0 0 1 0 0 0 0 1
r4,5 0 0 0 1 1 0 0 0
r4,6 0 0 0 1 0 1 0 0
0 0 0 0 1 1 0 0
Xi 2 2 3 2 3 3 2 1
а)
r2,7
r1,6
r3,8
r1,5
r4,5
r4,6
r3,7
x5
r5,6
x6
x7
x8
G=<X;r>
а)



 r1,5
r1,5

 r5,6
r5,6







 x1
x2
r2,3
x3
x4
x1
x2
r2,3
x3
x4








в) h x1 x2 x3 x4 x5 x6 x7 x8
1 0 0 0 1 0 0 0
r1,6 1 0 0 0 0 1 0 0
r3,7 0 0 1 0 0 0 1 0
r3,8 0 0 1 0 0 0 0 1
0 0 0 0 1 1 0 0
Xi 2 0 2 0 2 2 1 1
г) x1
x2
x3
x4
r1,5
r1,6
r3,7
r3,8
x5
r5,6
x6
x7
x8
G=<X;r>



 r1,5
r1,5

 r5,6
r5,6













Удаление вершины графа G=<X;r>. Пусть дан граф (см. рис. 32а), у которого необходимо удалить вершины x2,x4. Удаление вершин и поиск инцидентных им рёбер удобно выполнять по матрице инциденции. Если в результате удаления вершины в строке матрицы инциденции будет одна “1”, то данную строку, являющуюся образом ребра или дуги, нужно удалить. В результате будет получена новая матрица инциденции, являющаяся образом подграфа G=<X;r> графа G=<X;r>. На рис. 32 показан процесс удаления вершин графа.
а)
x1
x2
r2,3
x3
x4
r2,7
r1,6
r3,8
r1,5
r3,7
r4,5
x5
r5,6
x6
x7
x8
G=<X;r>
г)
x1
x3
x5
x6
x7
x8
G=<X;r>
Рис. 32. Удаление вершин графа.
б) h x1 x2 x3 x4 x5 x6 x7 x8
1 0 0 0 1 0 0 0
r1,6 1 0 0 0 0 1 0 0
r2,3 0 1 1 0 0 0 0 0
r2,7 0 1 0 0 0 0 1 0
r3,7 0 0 1 0 0 0 1 0
r3,8 0 0 1 0 0 0 0 1
r4,5 0 0 0 1 1 0 0 0
r4,6 0 0 0 1 0 1 0 0
0 0 0 0 1 1 0 0
Xi 2 2 3 2 3 3 2 1
в) h x1 x3 x5 x6 x7 x8
1 0 1 0 0 0
r1,6 1 0 0 1 0 0
r3,7 0 1 0 0 1 0
r3,8 0 1 0 0 0 1
0 0 1 1 0 0
Xi 2 2 2 2 1 1













 r4,6
r4,6















 r1,5
r1,5

 r5,6
r5,6



 r1,5
r1,5

 r5,6
r5,6
Поиск числа внутренней устойчивости графа G=<X;r>. Пусть дан граф G=<X;r>, который может быть образом строительной конструкции, для которой необходимо найти наибольшее число несмежных вершин (см. рис. 33а)). Для этого удобно воспользоваться таблицами отображений, которые необходимо дополнить столбцом несмежных (hxi) вершин графа G (см. рис. 33б)). Если по этой таблице найдутся несмежные вершины, то нужно сформировать двухэлементные множества из числа несмежных вершин и найти им образ hxi,xj и hxi,xj. Для формирования двухэлементных множеств несмежных вершин использовать процедуру сочетания из элементов x и hxi. Найти отображение двухэлементных множеств: hxi,xj и hxi,xj. Если найдутся элементы hxi,xj, то сформировать трёхэлементные множества из вершин, принадлежащих {xi,xj} и hxi,xj. Найти отображение трёхэлементных множеств {xi,xj,xk} и hxi,xj,xk. Если найдутся элементы hxi,xj,xk, то сформировать четырёхэлементные множества и т.д. Для нашего примера трёхэлементные множества hxi,xj,xk определяют {hxi,xj,xk}=0. Поэтому наибольшее подмножество несмежных вершин для данного графа содержит не более трёх вершин исходного графа. Множество несмежных вершин графа G содержит шесть подмножеств, среди которых два подмножества имеют наибольшее число вершин. На рис. 33 дан процесс поиска числа внутренней устойчивости графа.
x3
x5
x6
x7
в)
{xi;xj}
h(xi;xj)
h(xi;xj)
x1;x5
x2;x3;x4;x7
x6
x1;x6
x2;x3;x4;x7
x5
x1;x7
x2;x3;x4;x5;x6
x2;x4
x1;x3;x5;x6
x7
x2;x6
x1;x3;x4;x5;x7
x2;x7
x1;x3;x5;x6
x4
x3;x7
x1;x2;x4;x5;x6
x4;x5
x1;x2;x3;x6;x7
x4;x7
x1;x3;x5;x6
x2
x5;x6
x2;x3;x4;x7
x1
б)
xi
hXi
hXi
x1
x2;x3;x4
x5;x6;x7
x2
x1;x3;x5
x4;x6;x7
x3
x1;x2;x4;x5;x6
x7
x4
x1;x3;x6
x2;x5;x7
x5
x2;x3;x7
x1;x4;x6
x6
x3;x4;x7
x1;x2;x5
x7
x5;x6
x1;x2;x3;x4
г)
{xi;xj;xk}
h(xi;xj;xk)
h(xi;xj;xk)
x1;x5;x6
x2;x3;x4;x7
x2;x4;x7
x1;x3;x5;x6
 x1
x1

 а)
а)



 x2
x4
x2
x4







д) S={{x1;x7};{x2;x6};{x3;x7}; {x4;x5};{x1;x5;x6};{x2;x4;x7}}.
(G)=maxi{|Si|}=3.
Рис. 33. Поиск внутренней усточивости графа.
Поиск внешней устойчивости графа G=<X;r>. Пусть дан граф G=<X;r>, для которого необходимо найти наименьшее число вершин, смежных со всеми остальными вершинами (см. рис. 34а)). Для этого также следует воспользоваться таблицами отображений и дополнить их столбцом несмежных вершин hxi(см. рис. 34б)). При наличии несмежных вершин, т.е. вершин, принадлежащих hxi, сформировать двухэлементные подмножества {xi;xj} из всех вершин исходного графа, т.е. найти комбинаторные объекты сочетания из n элементов по два. Для двухэлементных подмножеств {xi;xj} найти множества элементов, принадлежащих hxi,xj и hxi,xj. Если найдётся {hxi,xj}=, то процесс окончен, в противном случае - перейти к формированию трёхэлементных подмножеств исходного множества вершин и т.д. Наименьшее число вершин графа G=<X;r>, смежных со всеми остальными вершинами, равно двум, а число таких подмножеств вершин равно шести. Выбор одного из подмножеств вершин внешней устойчивости определяется другой задачей. Множество вершин графа, определяющих внешнюю и внутреннюю его устойчивости, формирует ядро графа. Для данного графа ядром является одно из трёх подмножеств {{x1;x7};{x2;x6};{x3;x7};{x4;x5}}, выбор которого также определяется какой-то другой задачей. Процесс поиска внешней устойчивости показан на рис. 34.
x3
x5
x6
x7
 x1
x1

 а)
а)


 x2
x4
x2
x4








в)
{xi;xj}
h(xi;xj)
h(xi;xj)
x1;x2
x3;x4;x5
x6;x7
x1;x3
x2;x4;x5;x6
x7
x1;x4
x2;x3;x6
x5;x7
x1;x5
x2;x3;x6
x7
x1;x6
x2;x3;x4;x7
x5
x1;x7
x2;x3;x4;x5;x6
x2;x3
x1;x4;x5;x6
x7
x2;x4
x1;x3;x5;x6
x7
x2;x5
x1;x3;x7
x4;x6
x2;x6
x1;x3;x4;x5;x7
x2;x7
x1;x3;x5;x6
x4
x3;x4
x1;x2;x5;x6
x7
x3;x5
x1;x2;x4;x6;x7
x3;x6
x1;x2;x4;x5;x7
x3;x7
x1;x2;x4;x5;x6
x4;x5
x1;x2;x3;x6;x7
x4;x6
x1;x3;x7
x2;x5
x4;x7
x1;x3;x5;x6
x2
x5;x6
x2;x3;x4;x7
x1
x5;x7
x2;x3;x6
x1;x4
x6;x7
x3;x4;x5
x1;x2
б)
xi
hXi
hXi
x1
x2;x3;x4
x5;x6;x7
x2
x1;x3;x5
x4;x6;x7
x3
x1;x2;x4;x5;x6
x7
x4
x1;x3;x6
x2;x5;x7
x5
x2;x3;x7
x1;x4;x6
x6
x3;x4;x7
x1;x2;x5
x7
x5;x6
x1;x2;x3;x4
T={{x1;x7};{x2;x6};{x3;x5}; {x3;x6};{x3;x7};{x4;x5}}
(G)=mini{|Ti|}=2.
Ядро={{x1;x7};{x2;x6};{x3;x7};
{x4;x5}}.
Рис. 34. Поиск внешней устойчивости графа.
3.3.2. Бинарные операции.
При исполнении операций над двумя графами G1=<X1;r1> и G2=<X2;r2> следует обратить внимание на наличие общих элементов, принадлежащих X1 и X2 или r1 и r2. Этот анализ позволяет выделить три варианта:
-
Вершины и рёбра (дуги) графов на имеют общих элементов, т.е. (X1X2)= и (r1r2)=;
-
Вершины графов имеют общие элементы, а рёбра (дуги) - нет, т.е. (X1X2) и (r1r2)=;
-
Вершины и рёбра (дуги) графов имеют общие элементы, т.е. (X1X2) и (r1r2);
Для каждого из вариантов результат применения теоретико-множественной операции будет формировать граф, отличный от других вариантов.
Объединение графов G1=<X1;r1> и G2=<X2;r2> есть граф G=<X;r>, для которого X=(X1X2) и r=(r1r2). Объединенние двух графов обозначается как G=(G1G2). На рис. 35 дана иллюстрация этой операции для трёх вариантов. Для исполнения этой операции можно воспользоваться матрицами инциденции и матрицами смежности. Матрица смежности для графа G=<X;r> будет иметь число строк и столбцов равным |X|=|X1X2|, а элементы матрицы определяются соотношением: ri,j=ri,j(1) ri,j(2).
а
G1
x1
x3
x7
x6
x1
x3
x7
x6
б
x1
x3
x3
x6
x1
x3
x6
в
G
x1
x3
x1
x4
x1
x3
Рис. 35. Объединение двух
графов.





 )
x2
x4
x5
x2
x4
x5
)
x2
x4
x5
x2
x4
x5



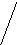


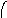



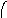

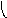
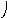

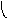
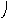
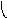
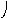
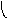
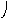 G2
G
G2
G















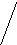





 )
x2
x4
x5
x2
x4
x5
)
x2
x4
x5
x2
x4
x5






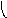
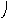

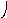 G1
G1

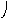
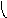
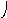
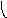 G2
G
G2
G
















 )
x2
x2
x3
x2
x4
)
x2
x2
x3
x2
x4






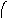

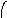

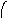

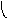
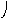

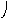 G1
G1
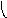


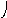
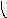 G2
G2









Пересечение графов G1=<X1;r1> и G2=<X2;r2> есть граф G=<X;r>, для которого X=(X1X2) и r=(r1r2). Пересечение двух графов обозначается как G=(G1G2). На рис. 36 дана иллюстрация этой операции для трёх вариантов. Для исполнения этой операции также можно воспользоваться матрицами инциденции и матрицами смежности. Матрица смежности для графа G=<X;r> будет иметь число строк и столбцов равным |X|=|X1X2|, а элементы матрицы определяются соотношением: ri,j=ri,j(1)ri,j(2).
а
x1
x3
x7
x6
б
G
x3
x1
x3
x3
x6
в
x1
x3
x1
x4
x1
x3


 )
x2
x4
x5
)
x2
x4
x5

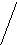




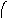

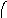
 G
G
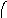




 G1
G1
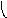

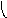
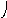
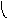 G2
G2







 )
x2
x4
x5
)
x2
x4
x5










 G1
G1
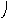
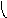 G2
G2









 )
x2
x2
x3
x2
)
x2
x2
x3
x2







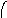

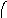

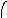


 G1
G1
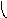
 G2
G
G2
G








Рис. 36. Пересечение двух графов.
Композиция графов G1=<X1;r1> и G2=<X2;r2> есть граф G=<X;r>, для которого X(X1X2), а ri,jr ориентирована от вершин графа G1 к вершинам графа G2 и существует тогда и только тогда, когда есть хотя бы одна вершина xk, принадлежащая двум графам G1 и G2, что обеспечивает маршрут через вершину xk , с началом маршрута в xi (1)X1 и концом в xj (2)X2. Композиция двух графов обозначается как G=(G1G2). Матрица смежности графа G=<X;r> имеет число строк и столбцов |X||X1X2|, а элементы матрицы определяются соотношением:
ri,j= k=1n(ri,k(1)rk,j(2)).
На рис. 37 дана иллюстрация этой операции для трёх вариантов.
а
G
x1
x3
x7
x6
б
G
x1
x3
x3
x6
x6
в
G
G1
x1
x3
x1
x4
x4
x3

 )
x2
x4
x5
)
x2
x4
x5










 G1
G1

 G2
G2








 )
x2
x4
x5
x2
)
x2
x4
x5
x2









 x1
x4
x1
x4


 G1
G1

 G2
G2














 )
x2
x2
x3
x1
x2
)
x2
x2
x3
x1
x2













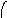

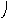

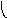
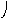
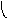
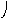
 G2
G2












Модульное произведение графов G1=<X1;r1> и G2=<X2;r2> есть граф G=<X;r>, множество вершин которого X определяется прямым произведением (xi(1);xj(2))(X1X2), а множество рёбер ((xi(1);xj(2));…;(xk(1); xl (2)))r существует тогда и только тогда, когда в графах G1 и G2 есть соответственно рёбра (xi(1);xk(1))r1 и (xj(2);xl(2))r2. Модульное произведение обозначается как G=(G1G2). Для поиска смежности вершин графа G удобно использовать таблицы отображения вершин графов G1 и G2 и составить таблицу отображения для (xi(1);xj(2))X. Элементы таблицы отображения следует заполнить по правилу:
h(xi(1),xj(2))={(hXi(1)hXj (2))}, где
hXi(1)={x(1)}X1, hXi(2)={x(2)}X2.
По результатам вычислений составить матрицу смежности графа G=<X;r>. На рис. 38 показан процесс вычисления модульного произведения двух неориентированных графов.
а
hXi(1)
x1(1)
x2(1)
x2(1)
x1(1);x3(1)
x2(1)
x1(1)
x3(1)
xj(2)
hXi(2)
x1(2)
x2(2)
x2(2)
x1(2)
x1(2)


 )G1
x2(1)
)G1
x2(1)
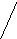 xi(1)
xi(1)
 x3(1)
x3(1)

 G2
x2(2)
G2
x2(2)

б)
(xi(1);xj(2))
h(xi(1);xj(2))
(x1(1);x1(2))
(x2(1);x2(2))
(x2(1);x1(2))
(x1(1);x2(2));(x3(1);x2(2))
(x3(1);x1(2))
(x2(1);x2(2))
(x1(1);x2(2))
(x2(1);x1(2))
(x2(1);x2(2))
(x1(1);x1(2));(x3(1);x1(2))
(x3(1);x2(2))
(x2(1);x1(2))
в) r
(x1(1);
x1(2))
(x2(1);
x1(2))
(x3(1);
x1(2))
(x1(1);
x2(2))
(x2(1);
x2(2))
(x3(1);
x2(2))
0
0
0
0
1
0
(x2(1);x1(2))
0
0
0
1
0
1
(x3(1);x1(2))
0
0
0
0
1
0
(x1(1);x2(2))
0
1
0
0
0
0
(x2(1);x2(2))
1
0
1
0
0
0
0
1
0
0
0
0



 (x1(1);x1(2))
(x1(1);x1(2))

 (x3(1);x2(2))
(x3(1);x2(2))
г
x1(1)
x3(1)
x1(2)
(x1(1);x2(2))
(x2(1);x2(2))
(x3(1);x2(2))





 )
x2(1)
x2(2)
(x1(1);x1(2))
(x2(1);x1(2))
(x3(1);x1(2))
)
x2(1)
x2(2)
(x1(1);x1(2))
(x2(1);x1(2))
(x3(1);x1(2))







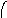

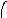

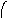

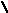
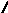


 G1
G1
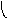
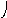
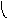
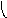 G2
G
G2
G





Декартова сумма графов G1=<X1;r1> и G2=<X2;r2> есть граф G=<X;r>, множество вершин которого X определяется также прямым произведением (xi(1);xj(2))(X1X2), а множество рёбер ((xi(1);xj(2));…(xk(1); xl (2)))r существует тогда и только тогда, когда существует только рёбро (xi(1);xk(1))r1 или только ребро (xj(2);xl(2))r2. Декартова сумма двух графов обозначается как G=(G1G2). Для поиска смежности вершин графа G также удобно использовать таблицы отображения вершин графов G1 и G2 и составить таблицу отображения для графа G. Элементы таблицы отображения графа G определяются по правилу:
h(Xi(1),Xj(2))={(hXi(1)xj(2))}{(xi(1)hXj(2))}, где
hXi(1)={x(1)}X1, hXi(2)={x(2)}X2, - знак исключающего или.
По результатам вычислений (xi(1);xj(2)) заполнить таблицу отображения для графа G, затем составить матрицу смежности графа G=<X;r>. На рис. 39 показан процесс вычисления декартовой суммы двух неориентированных графов.
xj(2) hXj(2) x1(2) x2(2) x2(2) x1(2)
x1(2)

 G2
x2(2)
G2
x2(2)

а
hXi(1)
x1(1)
x2(1)
x2(1)
x1(1);x3(1)
x2(1)
x1(1)
x3(1)

 )G1
x2(1)
)G1
x2(1)

 xi(1)
xi(1)
 xx3(1)
xx3(1)
б)
(xi(1);xj(2))
h(xi(1);xj(2))
(x1(1);x1(2))
(x2(1);x1(2))(x1(1);x2(2))
(x2(1);x1(2))
((x1(1);x1(2))(x3(1);x1(2)))(x2(1);x2(2))
(x3(1);x1(2))
(x2(1);x1(2))(x3(1);x2(2))
(x1(1);x2(2))
(x2(1);x2(2))(x1(1);x1(2))
(x2(1);x2(2))
((x1(1);x2(2))(x3(1);x2(2)))(x2(1);x1(2))
(x3(1);x2(2))
(x2(1);x2(2))
(x3(1);x1(2))
в) r
(x1(1);
x1(2))
(x2(1);
x1(2))
(x3(1);
x1(2))
(x1(1);
x2(2))
(x2(1);
x2(2))
(x3(1);
x2(2))
0
1
0
1
0
0
(x2(1);x1(2))
1
0
1
0
1
0
(x3(1);x1(2))
0
1
0
0
0
1
(x1(1);x2(2))
1
0
0
0
1
0
(x2(1);x2(2))
0
1
0
1
0
1
0
0
1
0
1
0



 (x1(1);x1(2))
(x1(1);x1(2))

 (x3(1);x2(2))
(x3(1);x2(2))
г
x1(1)
x3(1)
x1(2)
(x1(1);x2(2))
(x2(1);x2(2))
(x3(1);x2(2))




 )
x2(1)
x2(2)
(x1(1);x1(2))
(x2(1);x1(2))
(x3(1);x1(2))
)
x2(1)
x2(2)
(x1(1);x1(2))
(x2(1);x1(2))
(x3(1);x1(2))










 G1
G1
 G2
G
G2
G






Изоморфизм графов G1=<X1;r1> и G2=<X2;r2>. Поскольку графы могут быть заданы различным способом: таблицами отношений или отображений, матрицами инциденции или смежности, графическими рисунками или чертежами, то вид и форма описания существенно зависят от исполнителя. Поэтому трудно иногда понять одинаковы ли предъявленные графы. Одинаковость состава и структуры графов определяется отношением изоморфизма.
Пусть даны два графа G1=<X1;r1> и G2=<X2;r2> и дано взаимооднозначное отображение на множестве вершин и рёбер графов, т.е.
X1X2 и -1X1 X2,
r1r2 и -1r1 r2.
а)
x1
x2
x3
x4
x5
x6
б)
a e
b
d
в)
1 6
5
2
4
3
Рис. 40. Изоморфизм графов.

























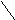
 f
c
f
c












Если такой изоморфизм существует, то графы G1 и G2 изоморфны, и оба они могут быть представлены одинаковыми матрицами инциденции или смежности.
R
x1
x2
x3
x4
x5
x6
0 0 0 1 1 1
x2 0 0 0 1 1 1
x3 0 0 0 1 1 1
x4 1 1 1 0 0 0
x5 1 1 1 0 0 0
1 1 1 0 0 0
I 3 3 3 3 3 3
R a b c d e f 0 1 0 1 0 1 b 1 0 1 0 1 0 c 0 1 0 1 0 1 d 1 0 1 0 1 0 e 0 1 0 1 0 1 1 0 1 0 1 0
I 3 3 3 3 3 3
R 1 2 3 4 5 6 0 1 0 1 1 0 2 1 0 1 0 0 1 3 0 1 0 1 1 0 4 1 0 1 0 0 1 5 1 0 1 0 0 1 0 1 0 1 1 0
I 3 3 3 3 3 3



 x1
x1

 x6
x6



 a
a

 f
f



 1
1

 6
6
Отношение изоморфизма рефлексивно, симметрично и транзитивно, т.е. является отношением эквиваленции. Следовательно, отношение изоморфизма разбивает всё множество графов на непустые и попарно непересекающие классы эквиваленции изоморфных графов.
Необходимыми условиями изоморфизма графов являются: равенство числа вершин и рёбер, одинаковость числа петель и набора степеней вершин графов, а достаточными условиями - одинаковость матриц инциденции или смежности графов. Чтобы проверить одинаковость матриц инциденции или смежности графов необходимо для n-вершинных графов выполнить n! перестановок строк и столбцов одного графа, каждый раз сравнивая с содержанием матрицы второго графа.
На рис. 40 дан пример изоморфизма трёх графов. Матрицы смежности каждого графа содержат по шесть вершин и девять рёбер.
Набор степеней вершин у всех графов также одинаков. Кстати, графы, у которых все вершины имеют одинаковую степень, называют однородными. Для проверки совместимости второго графа (см. рис. 40б)) с первым (см. рис. 40а)) наобходимо выполнить перестановки строк и столбцов матрицы смежности второго графа. Просмотр всех вариантов требует исполнения 720 перестановок. Однако, если поменять местами вершины b и e, поменяв местами соответствующие столбцы и строки матрицы смежности, то новая матрица второго графа будет тождественна матрице смежности первого графа. Для проверки совместимости третьего графа(см. рис. 40в)) также необходимо выполнить перестановки строк и столбцов матрицы смежности. Очевидно, если поменять местами вершины 2 и 6, соответственно столбцы и строки матрицы смежности, то получим матрицу третьего графа тождественную матрице первого графа. Итак, доказана изоморфность всех трёх графов, т.е. сформирован класс эквиваленции для трёх графов.
Контрольные вопросы и задачи.
1.Найти дополнение к графу
x1 x2


 х4
х4



 x5 x3
x5 x3

x2 x4
x6
x8
x10
x7





 x1 x3 x5
x9
x11
x1 x3 x5
x9
x11












3. Найти число компонент связности графа
x3 x7 x x
x5







 2
x4
x8
2
x4
x8




 x6
x6


 1
x10
x9
1
x10
x9
а)
б )








 x1 x3
x5
x1 x3
x5


 x0
x7
x0
x7


 x2 x4
x6
x2 x4
x6






 x1 x3
x5
x1 x3
x5


 x0
x7
x0
x7


 x2 x4
x6
x2 x4
x6
5. Найти объединение и пересечение двух графов
а) граф G1=<X;r1>
|
ri |
r11 |
r12 |
r13 |
r14 |
r15 |
r16 |
|
(xi;xj) |
(x1;x3) |
(x2;x4) |
(x2;x5) |
(x3;x4) |
(x3;x5) |
(x4;x5) |
б) граф G2=<X;r2>
|
r11 |
r21 |
r22 |
r23 |
r24 |
r25 |
r26 |
|
(xi;xj) |
(x1;x2) |
(x1;x5) |
(x1;x4) |
(x2;x3) |
(x2;x4) |
(x2;x5) |
6. Найти модульное произведение двух графов
х1(1)
х4(1)
х1(2)
х3(2)








 х2(1)
х3(1) х2(2)
х2(1)
х3(1) х2(2)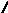
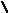
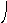
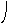
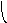


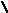




8. Изоморфны ли графы
а)
х1
x2
a б )
c





 х1
х1





 х6 х2
х5
х6 х2
х5



 х3
х4
х3
х4



 х5
х5

 х3
х6
х3
х6

 х4
х4


 a d
a d



 e
b
e
b



 b e
d c
b e
d c
3.4. Алгоритм построения покрывающего дерева.
Остов графа G=<X;r> есть связанный суграф в виде дерева без циклов, петель и кратных ребер, опирающийся на все множество вершин исходного графа, т.е. G`=<X;r`>, где r`r. Так как остов опирается на все верщины графа G, то его называют покрывающим остовом или деревом. Остов, покрывающий n вершин графа G, содержит (n-1) ребро.
Задача поиска покрывающего остова G`=<X;r`> возникает при разметке модулей баз данных, при организации сложных программных комплексов, при проектировании трасс вычислительных сетей и транспортных систем.
Суть алгоритма заключена в просмотре ребер графа в произвольном порядке, формировании фрагмента остова графа, т.е. G`=<X`;r`>, где Х`Х - подмножество вершин графа и r`r - подмножество ребер, включаемых во фрагмент:
шаг 1: выбрать любое ребро, не являющееся петлей, сформировать фрагмент, а концевые вершины ребра включить в подмножество Х`;
шаг 2: выбрать любое ребро, не принадлежащее фрагменту и не являющееся петлей:
а) если одна концевая вершина выбранного ребра принадлежит фрагменту, то вторую концевую вершину включить в подмножество Х`, а ребро включить в фрагмент остова G`=<X`;r`>;
б) если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова;
в) если коцевые вершины принадлежат различным остовам, то соединить фрагменты и вернуться к шагу 2;
шаг 3: если все вершины графа вошли во фрагмент остова, т.е. Х`=Х, то конец, иначе перейти у шагу 2.
х4
х3
х6




 G=<X;r>
х2
х5
G=<X;r>
х2
х5

 х1
х7
х1
х7




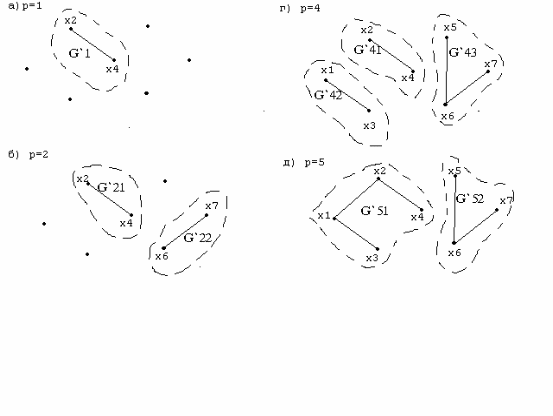
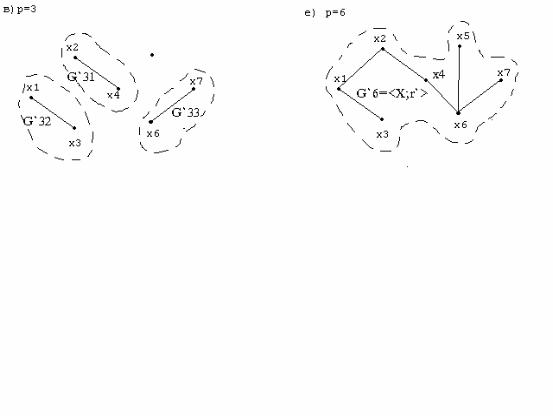
Рис. 41. Построение покрывающего остова графа.
На рис. 41 показан процесс поиска покрывающего остова графа, где p-шаг итерации. На первом шаге итерации произвольно выбрано ребро (х2;х4), на втором шаге - (х6;х7), на третьем шаге - (х1;х3). При этом согласно пункту алгоритма 2б) формировались независимые фрагменты остова G`31, G`32 и G`33. На четвертом шаге при выборе ребра (х5;х6) согласно пункту 2а) алгоритма сформирован фрагмент G`43 типа дерево. На пятом шаге при выборе ребра (х1;х2) согласно пункту 2в) произошло слияние двух фрагментов G`41 и G`42. И наконец, на шестом шаге итерации при выборе ребра (х4;х6) сформирован остов графа G`6=<X;r`>.
Следует обратить внимание, что число итераций равно числу присоединяемых к фрагменту ребер, а их количество должно быть меньше числа вершин на единицу.
Иногда возникает задача не только найти покрывающий остов, но использовать определенный набор покрывающих ребер. Для этого необходимо прежде всего определить цикломатическое число (G), которое позволит знать число ребер, удаление которых ликвидирует циклы. Далее, используя элементы комбинаторики, найти число вариантов формирования остова.
Для графа, приведенного на рис. 42 цикломатическое число равно (G)=m-n+(G)=5-4+1=2.
х1
х4
х3
G=<X;r>
х1 G`1
х4
х3 д)
х2
х1
G`5
х4
х3 б)
х2
х1
G`2
х3
е)
х1
G`6
х4
х3
в)
х2
х1 G`3
х4
х3
ж)
х2
х1 G`7
х4
х3
г)
х2
х1
G`4
х4
х3
з)
х2
х1 G`8
х4
х3
Рис. 42. Остовы графа
















 х2
х2


 а)
х2
а)
х2













 х4
х4
 х2
х2

























Число возможных конфигураций для графа, опирающегося на четыре вершины и три ребра, определяется числом сочетаний из пяти по три, т.е.
)
(
)
(
=
=
m
n
5 3
5!/(3!2!)=10.
Две конфигурации сохраняют циклы в графе G`=<X;r`>. Это графы использующие ребра r`1={(х1;х2);(х2;х3);(х3;х1)} и r`2={(х2;х3);(х3;х4);(х4;х2)}. Оставшиеся восемь конфигураций остовов позволяют выбрать один, но по иным критериям. Например, по надежности, стоимости, вероятности безотказной работы.
3.5. Алгоритм построения остова минимального веса.
Решение такой задачи имеет большое значение в проектировании вычислительных систем с минимальной протяженностью каналов передачи информации, в организации грузоперевозок по транспортной сети при минимальных финансовых или энергетических затратах.
Основная идея нахождения остова минимального веса состоит в следующем: если есть некоторый фрагмент остова G`=<X`;r`> и ребро или дуга минимального веса l(хi;хj), одна из концевых вершин которого хi принадлежит фрагменту G`, то включить в фрагмент вторую вершину ребра хj и само ребро l(хi;хj); процедуру продолжать до включения во фрагмент (n-1) ребра или дуги графа, где n-число его вершин. Фрагментом остова является суграф в виде дерева.
Эта идея реализуется двумя алгоритмами.
Алгоритм Дейкстра. Предусматривает заданной начальную вершину фрагмента и последовательное присоединение ребер или дуг графа, имеющих минимальный вес, к фрагменту остова. Такая постановка задачи характерна для заданной корневой вершины базы данных, для заданного узла транспортной системы, для заданного места установки сервера локальной вычислительной сети и т.п.
шаг 1: выбрать ребро минимального веса, смежное начальной вершине и сформировать фрагмент G`=<X`;r`>, включив вторую концевую вершину в подмножество Х`;
шаг 2: выбрать ребро минимального веса, смежное вершинам фрагмента и не являющееся петлей:
а) если вторая концевая вершина не принадлежит фрагменту, то включить ее в подмножество Х`, ребро включить в фрагмент остова G`=<X`;r`>;
б) если вторая концевая вершина принадлежит фрагменту, что формирует цикл, то отбросить данное ребро из анализа;
шаг 3: если все вершины графа вошли во фрагмент остова, т.е. Х`=Х, то конец, иначе перейти к шагу 2.
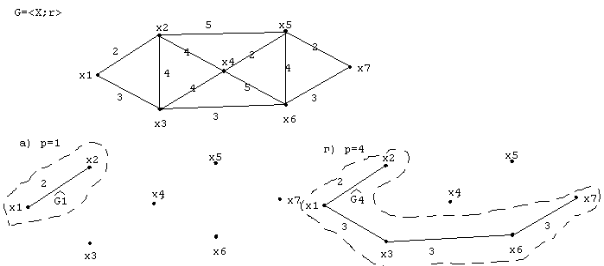
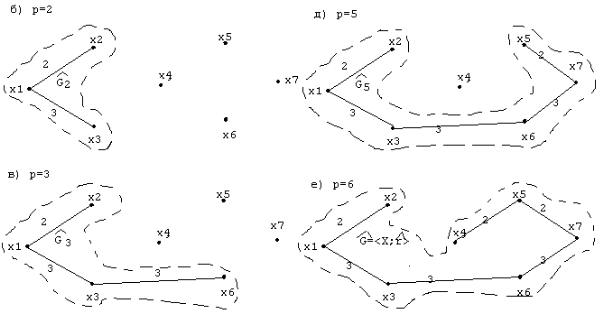
Рис. 43. Построение остова графа по алгоритму Дейкстра.
На рис. 43 показан процесс построения остова графа минимального веса по алгоритму Дейкстра для начальной вершины x1, где p-шаг итерации. Максимальная протяженность минимального остова равна 15 условным единицам.
Алгоритм Краскала. При работе по этому алгоритму необходимо установить частичный порядок на ребрах графа, поставив на первое место ребро минимального веса, а на последнее - максимального веса. Последовательно присоединяя к фрагменту по одному ребру формируют фрагмент остова минимального веса.
шаг 1: выбрать ребро минимального веса, не являющееся петлей, сформировать фрагмент остова G`=<X`;r`>, а концевые вершины ребра включить в подмножество Х`Х; если несколько ребер имеют одинаковый вес, то выбрать ребро произвольно;
шаг 2: выбрать ребро минимального веса, не являющееся петлей и не принадлежащее фрагменту:
шаг 2.1: если фрагменту принадлежит одна вершина ребра, то вторую концевую вершину включить в подмножество Х`, ребро включить в фрагмент остова Gp`=<X`;r`>;
шаг 2.2: если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова;
шаг 2.3: если коцевые вершины принадлежат резличным остовам, то соединить фрагменты и вернуться к шагу 2; если ребра имеют одинаковый вес, то выбрать ребро произвольно;
шаг 3: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 2.
На рис. 44 показан процесс построения остова графа минимального веса по алгоритму Краскала. Максимальная протяженность минимального остова также равна 15 условным единицам, что подтверждает единое решение о минимальном весе для двух алгоритмов (Дейкстра и Краскала).

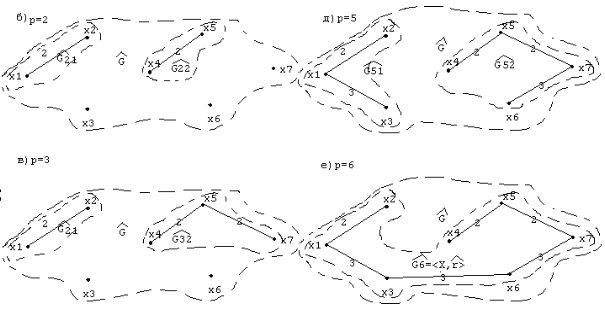 Рис.
44. Построение остова графа по алгоритму
Краскала.
Рис.
44. Построение остова графа по алгоритму
Краскала.
На каждом этапе построения остова графа формируется суграф G` графа G.
В [7] даны примеры использования алгоритмов поиска остова графа минимального веса и программное обеспечение. Так в одном из примеров решается задача использования финансовых ресурсов отделом автомобильных дорог для проведения ремонтных работ на участках дорог, соединяющих n населенных пунктов. При этом длина каждого участка дороги соответствовала затратам на производство ремонтных работ.
В другом примере предложена схема прокладки телевизионных кабелей системы кабельного телевидения.
В третьем примере решается задача коммивояжера, который должен выехать из данного города, побывать в каждом из остальных (n-1) городов данного округа по одному разу. При этом известна длина маршрута между любой парой городов.


















 x1
x1
 x5
x5


 x1
x1
 x5
x5


 x1
x1
 x6
x6


 x1
x1
 x6
x6


 x1
x1
 x8
x8


 x1
x1
 x8
x8