
3.7. Алгоритм поиска максимального потока.
При обмене информацией между абонентами вычислительной сети, при параллельных вычислениях на многомашинном комплексе, когда решение задачи распределяется между несколькими процессорами, при использовании в вычислительной сети общей памяти, когда каждый процессор получает доступ к общим модулям на ограниченный отрезок времени, возникает задача передачи максимального объема информации в заданный отрезок времени.
При работе транспортной системы, когда осуществляется обмен транспотными единицами между узлами сети также возникает задача передачи максимального объема транспортных единиц за заданный отрезок времени.
При передаче энергии в электрических сетях, жидкости в различных трубопроводных системах также возникает задача передачи максимального объема энергии или вещества в заданный отрезок времени.
Объем информации, энергии или вещества, передаваемый от одного узла к другому, называют потоком и обозначают i,j.
Граф, являющийся образом транспортной системы, называют сетью. Особенностью сети является отсутствие петель и кратных дуг, ориентация всех отрезков линий, т.е. наличие дуг в графе, наличие вершины-истока и вершины-стока в сети.
Наибольший поток, который может пропустить дуга сети, называют пропускной способностью дуги и обозначают Сi,j.
Очевидно, что 0i,j Сi,j.
В вершине-истоке х0 величина потока есть сумма потоков по всем дугам, исходящим из вершины х0, т.е.=i0i+.
В вершине-стоке хk величина потока есть сумма потоков по всем дугам, заходящим в вершину хk, т.е.=iik-.
Для любой промежуточной вершины хi сумма исходящих потоков равна сумме заходящих потоков, т.е. jij+=kik-.
На рис. 47 показана условная сеть, содержащая вершину-исток х0, вершину-сток хk и две промежуточные вершины хi и хj. На каждой дуге в круглых скобках приведены обозначения потока и пропускной способности соответствующей дуги. При этом поток, подводимый к сети равен =(0i+0j), поток отводимый от сети равен =(ik+jk), поток из вершины хi в вершину хj равен ij. Для вершины хi имеем 0i=(ij+ik), для вершину хj - jk=(0j+ij).
Если множество вершин графа разбить на два непересекающихся подмножества, одно из которых содержит вершину-исток, а другое - вершину-сток, то множество дуг, соединяющих эти два множества, формируют разрез А, пропускная способность которого равна сумме пропускных способностей дуг. Таких разрезов может быть несколько. Очевидно, что величина максимального потока ограничена минимальной пропускной способностью разреза, т.е.
max=min{СAi}.
Для примера на рис. 47 приведена схема, объясняющая множество пропускных способностей разрезов. Для разреза А1 имеем Х^={x0} и X\Х^={хi;хj;хk}, для А2 - Х^={х0;хj} и X\Х^={хi;хk}, для А3 - Х^={х0;хi} и X\Х^={хj;хk}, для А4 - Х^={х0;хi;хj} и X\Х^={хk}.

(
A1 A3 xj A4 A2



 CA2 xi CA3 CA4
CA2 xi CA3 CA4

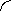 CA1
CA1 

 0i;C0i)
(ik;Cik)
0i;C0i)
(ik;Cik)



 x0 (ij;Cij)
xk
x0 (ij;Cij)
xk 
 (0j;C0j)
(jk;Cjk)
(0j;C0j)
(jk;Cjk)


Разрез
пропускная
способность
дуги Сi,j пропускная способность
С0,i С0,j Сi,j Сi,k Сj,k разреза СAi А1 1 1 0 0 0 С0,i+
С0,j А2 1 0 1 0 1 С0,i+Сi,j+Сj,k А3 0 1 1 1 0 С0,j+Сi,j+Сi,k А4 0 0 0 1 1 Сi,k+Сj,k
Рис. 47. Условная сеть и множество
разрезов.
Итак, максимальный поток в сети с ограниченной пропускной способностью можно находить, вычисляя пропускные способности всех разрезов и выбирая среди полученных значений минимальное. Однако при таком решении задачи остается неизвестным распределение потока по дугам графа.
Д ля
поиска распределения потока по дугам
графа разработано несколько алгоритмов,
особое место среди которых занимает
алгоритм Форда-Фалкерсона, суть которого
состоит в разметке вершин графа. Метка
вершины графа указывает на возможность
изменения потока через эту вершину и
указывает источник этого изменения. На
рис. 48 дан фрагмент сети,
объясняющий суть алгоритма.
ля
поиска распределения потока по дугам
графа разработано несколько алгоритмов,
особое место среди которых занимает
алгоритм Форда-Фалкерсона, суть которого
состоит в разметке вершин графа. Метка
вершины графа указывает на возможность
изменения потока через эту вершину и
указывает источник этого изменения. На
рис. 48 дан фрагмент сети,
объясняющий суть алгоритма.
xi
xj
xs
+si
+tj
xt
xi xj
si +s +i
tj -j
+t
Рис. 48. Пометка вершин сети.






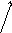











Е
 сли
по дуге (хs;хi) возможно
увеличение потока, т.е. si<Csi,
то вершину хi следует пометить +s
, что указывает на источник увеличения
потока. Если по дуге (хi;хj)
также возможно увеличение потока
ij<Cij,
то вершину хj пометить +i . Это
означает, что приращение потока si
пойдет по направлению дуги (хi;хj)
от вершины хs.
сли
по дуге (хs;хi) возможно
увеличение потока, т.е. si<Csi,
то вершину хi следует пометить +s
, что указывает на источник увеличения
потока. Если по дуге (хi;хj)
также возможно увеличение потока
ij<Cij,
то вершину хj пометить +i . Это
означает, что приращение потока si
пойдет по направлению дуги (хi;хj)
от вершины хs.
Е

 сли
по дуге (хt;хj) возможно
увеличение потока, т.е. tj<Ctj,
то вершину хj следует пометить +t
, что указывает на источник увеличения
потока. Однако, если вершина хj не
имеет пометки +i , то для
увеличения потока в фрагменте сети,
следует уменьшить поток в дуге (хi;хj)
и направить его далее по другим дугам
фрагмента на сток. Для указания вершины,
от которой необходимо уменьшить поток,
ставят пометку -j. Это означает что на
участке (хi;хj) поток должен
быть уменьшен на величину tj.
сли
по дуге (хt;хj) возможно
увеличение потока, т.е. tj<Ctj,
то вершину хj следует пометить +t
, что указывает на источник увеличения
потока. Однако, если вершина хj не
имеет пометки +i , то для
увеличения потока в фрагменте сети,
следует уменьшить поток в дуге (хi;хj)
и направить его далее по другим дугам
фрагмента на сток. Для указания вершины,
от которой необходимо уменьшить поток,
ставят пометку -j. Это означает что на
участке (хi;хj) поток должен
быть уменьшен на величину tj.
Следует отметить, что вершины хi и хj могут иметь одновременно по нескольку подходящих и отходящих дуг. В примере, показанном на рис. 48 одновременно при допустимых si и tj могут быть для вершины хj две метки +t и +i для вершины хi также две метки +s и -j, что свидетельствует о свободе выбора приращения потока либо на величину si, либо tj.
Если дуга (хs;хi) насыщена, т.е. si=Сsi, то метку “+s” у вершины хi ставить нельзя. Также, если насыщена дуга (хt;хj), т.е. tj=Сtj, то метку “+t” у вершины хj ставить нельзя.
Если вершина хj не помечена, то нельзя ставить метку “-j” у вершины хi. Когда обе вершины графа (хi и хj) не имеют меток, то это означает невозможность увеличения потока на дугах-стока. Так достигают максимального значения потока от двух вершин-истоков хs и хt по дугам-стока, исходящим из вершин хi и хj.
Алгоритм Форда-Фалкерсона.
шаг 1: присвоить всем вершинам графа индексы 0,1,2,...k; где 0-индекс вершины-истока графа, k -индекс вершины-стока графа;
шаг 2: присвоить начальной вершине метку “0”;
шаг 3: все непомеченные вершины хi, в которые идут ненасыщенные дуги из помеченной вершины хs, пометить индексом “+s”, что свидетельствует о возможности увеличения потока из вершины хs по дуге (хs;хi);
шаг 4: все непомеченные вершины хi, из которых идут дуги (насыщенные или ненасыщенные) в помеченную вершину хj, пометить индексом “-j”, что свидетельствует о возможности уменьшения потока в вершину хj по дуге (хi;хj);
шаг 5: если в результате этих операций окажется помеченной вершина-сток, то между начальной и конечной вершинами сети найдется маршрут, все вершины которого различны и с точностью до знака помечены индексами предыдущих вершин, формирующих переход, по которому можно увеличить поток, и перейти к шагу 6, иначе конец.
шаг 6: увеличить поток в маршруте, сформированном на шаге 5, на единицу и перейти к шагу 3.
Д ля
иллюстрации работы алгоритма распределения
максимального потока по дугам графа
рассмотрим граф (см. рис. 49а)). Каждой
дуге графа (хi;хj) приписаны
величина потока и пропускная способность
(ij;Сij).
Все расчеты по алгоритму сведены в две
таблицы. В таблице 14 на каждом шаге
итерации для каждой вершины графа
указаны возможные метки, формирующие
маршрут. В таблице 15 даны приращения
потока по дугам графа (хi;хj).
Насыщение дуги показано в таблице 15
знаком . Итак, в результате
выполнения первой итерации возможны
маршруты для увеличения потока на
единицу:1=(хk;х1;х0);
2=(хk;х2;х0);
3=(хk;х2;х3;х0);
4=(хk;х2;х3;х1;х0);
5=(хk;х3;х0);
6=(хk;х3;х1;х0),
из множества которых был выбран для
второй итерации маршрут 5.
При увеличении потока на единицу по
данному маршруту оказалась насыщенной
дуга (х3;хk). В результате
расстановки меток на второй итерации
возможны маршруты: 1=(хk;х1;х0);
2=(хk;х2;х0);
3=(хk;х2;х3;х0);
4=(хk;х2;х3;х1;х0),
из множества которых выбран маршрут
4. При увеличении
потока на единицу по данному маршруту
оказалась насыщенной дуга (х3;х2).
В результате расстановки меток на
третьей итерации возможны маршруты:
1=(хk;х1;х0);
2=(хk;х2;х0),
из которых выбрали маршрут 1.
При увеличении потока по этому маршруту
оказалась насыщенной дуга (х0;х1).
Следует отметить, что на этой итерации
не использовали метку у вершины х3.
В результате расстановки меток на
четвертом этапе вершина х3 помечена
+0, а вершина х1 не может быть
помечена “+0”, т.к. дуга (х0;х1)
-насыщена. Таблица 14 показывает возможность
для вершины х1 поставить метку-3,
что приведет к перераспределению потоков
в дугах графа, но общему увеличению.
Итак, на четвертом этапе имеем возможные
маршруты: 1=(хk;х1;-х3;х0);
2=(хk;х2;х0),
из которых выбран маршрут 1.
При перераспределении потоков (уменьшение
потока в дуге (х1;х3), насыщении
дуги (х0;х3)) удалось увеличить
поток еще на одну единицу. При установке
меток на пятой итерации разнообразие
маршрутов сведено к одному - 1=(хk;х1;х0).
ля
иллюстрации работы алгоритма распределения
максимального потока по дугам графа
рассмотрим граф (см. рис. 49а)). Каждой
дуге графа (хi;хj) приписаны
величина потока и пропускная способность
(ij;Сij).
Все расчеты по алгоритму сведены в две
таблицы. В таблице 14 на каждом шаге
итерации для каждой вершины графа
указаны возможные метки, формирующие
маршрут. В таблице 15 даны приращения
потока по дугам графа (хi;хj).
Насыщение дуги показано в таблице 15
знаком . Итак, в результате
выполнения первой итерации возможны
маршруты для увеличения потока на
единицу:1=(хk;х1;х0);
2=(хk;х2;х0);
3=(хk;х2;х3;х0);
4=(хk;х2;х3;х1;х0);
5=(хk;х3;х0);
6=(хk;х3;х1;х0),
из множества которых был выбран для
второй итерации маршрут 5.
При увеличении потока на единицу по
данному маршруту оказалась насыщенной
дуга (х3;хk). В результате
расстановки меток на второй итерации
возможны маршруты: 1=(хk;х1;х0);
2=(хk;х2;х0);
3=(хk;х2;х3;х0);
4=(хk;х2;х3;х1;х0),
из множества которых выбран маршрут
4. При увеличении
потока на единицу по данному маршруту
оказалась насыщенной дуга (х3;х2).
В результате расстановки меток на
третьей итерации возможны маршруты:
1=(хk;х1;х0);
2=(хk;х2;х0),
из которых выбрали маршрут 1.
При увеличении потока по этому маршруту
оказалась насыщенной дуга (х0;х1).
Следует отметить, что на этой итерации
не использовали метку у вершины х3.
В результате расстановки меток на
четвертом этапе вершина х3 помечена
+0, а вершина х1 не может быть
помечена “+0”, т.к. дуга (х0;х1)
-насыщена. Таблица 14 показывает возможность
для вершины х1 поставить метку-3,
что приведет к перераспределению потоков
в дугах графа, но общему увеличению.
Итак, на четвертом этапе имеем возможные
маршруты: 1=(хk;х1;-х3;х0);
2=(хk;х2;х0),
из которых выбран маршрут 1.
При перераспределении потоков (уменьшение
потока в дуге (х1;х3), насыщении
дуги (х0;х3)) удалось увеличить
поток еще на одну единицу. При установке
меток на пятой итерации разнообразие
маршрутов сведено к одному - 1=(хk;х1;х0).

а)
x1 (0;4) x3
(0;2) (0;3) (0;2)
x0 (0;1) xk
p=0 x2
x1
(0;4) x3
(0;2)
(1;2)
(1;3)
(0;3) 1=1
x0
(0;1) xk (0;1)
(0;2)
p=1 x2
в) x1
(0;4) x3
(2;2)
(0;2) (2;3)
(0;3) 2=2
x0
(0;1) xk (0;1)
(0;2)
p=2 x2
(1;2)
(2;2)
(2;3)
(0;3)
x0
(1;1) xk 3=3 (0;1)
(1;2)
p=3
x2
д) x1
(1;4) x3
(2;2)
(2;2)
(2;3)
(1;3)
x0
(1;1) xk 4=4 (0;1)
(1;2)
p=4 x2
x1
(1;4) x3
(2;2)
(2;2)
(3;3)
(2;3) 5=5
x0
(1;1) xk (0;1)
(1;2)
p=5
x2
x1
(0;4) x3
(2;2)
(2;2)
(3;3)
(2;3) 6=6
x0
(1;1) xk (1;1)
(2;2)
p=6
x2
Рис. 49. Максимальный поток в сети.












 =
= 0
(0;3) =0
0
(0;3) =0
 (0;1) (0;2 )
(0;1) (0;2 )



























 б)
б)



























 г)
x1 (1;4) x3
г)
x1 (1;4) x3








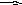






















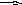









 е)
е)













 ж)
ж)
Таблица 14. хi шаг
итерации pi=i
1 2 3 4 5 6
х0 0 0 0 0 0 0
х1 +0 +0 +0 -3 - -
х2 +0;+3 +0;+3 +0 +0 +0 -
х3 +0;+1 +0;+1 +0;+1 +0 - -
хk +1;+2;+3 +1;+2 +1;+2 +1;+2 +2 -
Таблица 15. (хi;хj) Сij шаг
итерации
pi=i
1 2 3 4 5 6 2 0 0 1 2 2 2 1 0 0 0 0 0 1 3 1 2 2 2 3 3 (х1;х3) 4 0 0 1
0 0 (х1;хk) 3 0 0 0 1 2 2 2 0 0 1
1 2 1 0 0 1 1 1 1 (х3;хk) 2 1 2 2 2 2 2


 (х0;х1)
(х0;х1)
 (х0;х2)
(х0;х2)

 (х0;х3)
(х0;х3)
 (х2;хk)
(х2;хk)








 (х3;х2)
(х3;х2)
На последней шестой итерации =6, дуги (х0;х1), (х0;х2), (х0;х3), (х2;хk), (х3;х2), (х3;хk) - насыщены, невозможно поставить метки у вершин х1, х2, х3. Следовательно, нельзя поставить метку и у концевой вершины-стока хk.
В [7] даны алгоритмы поиска потока минимальной стоимости, алгоритмы дефекта, алгоритмы поиска максимального потока в неориентированной сети и при наличии большого числа истоков и стоков. Все алгоритмы подкреплены примерами и программными модулями для компьютера.
