
- •Матрица плотности. Чистые и смешанные состояния. Свойства диагональных матричных элементов матрицы плотности. Стационарные и нестационарные состояния. Уравнение фон Неймана.
- •Распределение Гиббса. Канонический и большой канонический ансамбль.
- •Теория атома гелия
- •Парагелий и ортогелий
- •Основная идея расчетов многоэлектронных систем
- •Молекула гелия
- •С войства операторов с учётом взаимосвязи с оператором
- •С войства операторов рождения и уничтожения фотонов
С войства операторов рождения и уничтожения фотонов
![]()
![]()
Каким образом возникает взаимодействие между Бозе и Ферми полями, можно узнать из принципа соответствия классической и квантовой механики. Достаточно заменить канонический импульс на кинетический:
![]()
Тогда гамильтониан квантовой частицы:
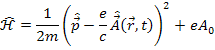

 Пример
(двухуровневая система).
Пример
(двухуровневая система).
Пусть электрон находится на внутреннем уровне с
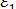 .
На
систему падает электромагнитное поле
(фотоны). Плотность излучения
.
На
систему падает электромагнитное поле
(фотоны). Плотность излучения  .
Произойдет поглощение одного фотона,
и электрон перейдет на внешний уровень.
Амплитуда вероятности перехода будет
пропорциональна
.
Произойдет поглощение одного фотона,
и электрон перейдет на внешний уровень.
Амплитуда вероятности перехода будет
пропорциональна 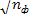 .
Сама вероятность такого процесса
.
Сама вероятность такого процесса 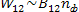 , где
, где 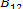 -
коэффициент индуцированного поглощения.
-
коэффициент индуцированного поглощения.
![]()
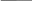
![]()

Пусть электрон находится на внешнем уровне с
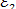 .
На
систему падает электромагнитное поле.
Так как поглотить фотон атом уже не
может, произойдет излучение фотона.
Амплитуда вероятности перехода будет
пропорциональна уже
.
На
систему падает электромагнитное поле.
Так как поглотить фотон атом уже не
может, произойдет излучение фотона.
Амплитуда вероятности перехода будет
пропорциональна уже 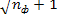 .
А вероятность процесса
.
А вероятность процесса 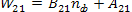 ,
где
,
где 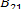 -коэффициент
индуцированного излучения, а
-коэффициент
индуцированного излучения, а  -
вероятность спонтанного излучения.
-
вероятность спонтанного излучения.
Часто приходится решать задачи в разных простейших ситуациях. Не обязательно это может быть одночастичное приближение, и мы можем пользоваться уравнением движения частицы с учетом квантовых свойств электромагнитного поля. Например, напишем релятивистское уравнение для электрона.
Гамильтониан:
![]()
Уравнение:
![]()
Оно описывает процессы взаимодействия заряженной частицы с квантовым полем излучения.
При взаимодействии Ферми частиц с Бозе полем, появляется ряд интересных эффектов.
Эффект смещения Лэмба. При движении частицы в кулоновском потенциале снимается вырождение s и p уровней за счет вакуумных флюктуаций.
Аномальный магнитный момент электрона.
![]()
Из
теории ![]() ,
а эксперимент показывает значение
отличное от 2. Это обусловлено воздействием
вакуумного поля на электрон, которое
меняет частоту прецессии.
,
а эксперимент показывает значение
отличное от 2. Это обусловлено воздействием
вакуумного поля на электрон, которое
меняет частоту прецессии.
