Простейшими звеньями, с помощью которых обеспечивается запаздывающая коррекция сар, являются звенья с перед. Функцией вида:

(2)

при К<1

ЛЧХ таких звеньев мажет быть представлена следующим образом.:

Видно, что в ЛЧХ можно выделить три зоны:

1.

2.

О чевидно, что наибольший эффект от введения такого звена может быть достигнут в том случае, если частота среза нескорректированной системы будет находится в высокочастотной зоне влияния этого устройства, т.е.

В этом случае достигается наибольшее уменьшение ординат лачх

нескорректированной системы до ; частота среза смещается влево, т.е. в ту область частот, где , как правило, меньше. Уменьшение ординат свидетельствует об уменьшении эффекта подавления возмущения прикладываемого за корректирующим устройством. Это является существенным минусом такой коррекции. Дополнительно, в этом случае имеем:

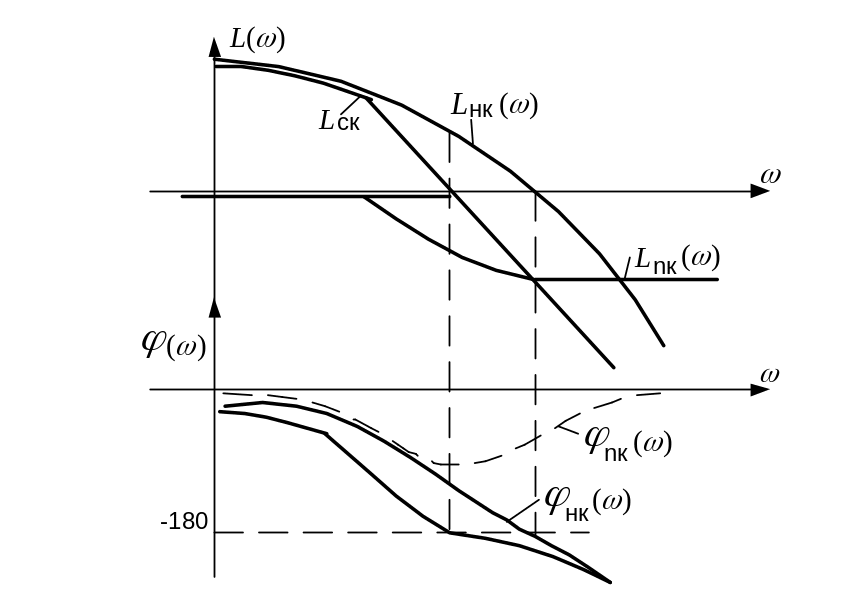
Ординаты ЛАЧХ при введении коррекции, уменьшились. Следовательно, по сравнению с применением опережающей коррекции ЛАЧХ замкнутой САР по отношению к возмущающей будут расположены выше и следовательно, влияние возмущения на регулируемую величину будет более существенно.

18. Комбинированная последовательная коррекция. (2 стр 41-42)

Простыми звеньями, с помощью которых обеспечивается комбинированная коррекция САР, являются звенья с перед. функцией вида:

(3)

Л ЧХ такого звена может быть изображена следующим образом:

ЛЧХ имеет 5 зон:

I ,

II ,

III ,

IV ,

V .

Очевидно, что наиболее целесообразной с точки зрения корректирования является зона IV. Наибольший эффект от применения такой коррекции может быть получен, если

Комбинированная коррекция сочетает в себе + и – как опережающей так и запаздывающей коррекции. Поскольку при комбинированной коррекции уменьшаются ординаты ЛАЧХ до частоты среза, то, следовательно, ей присущи недостатки запаздывающей коррек­ции. Выбор того или иного вида последовательной корректировки определяется порядков (общим) передаточной функции не скорректированной системы. Часто этот порядок определяется числом инерционных звеньев основного контура регулирования. Введение коррекции обеспечи­вает в определенном смысле компенсацию влияния инерционных звеньев.

Если в контуре регулирования имеется одно звено с "большой" постоянной времени , а остальные звенья - с относи­тельно малыми постоянными времени, то наиболее целесообразным является применение опережающей коррекции. Применение опережа­ющей коррекции является предпочтительнее, как уже отмечалось, и с точки зрения максимального ослабления влияния возмущающих воздействий.

19.Оценка качества регулирования (2 стр 43-44)

Показатели качества регулирования

Устойчивость САР является необходимым, но недостаточным условием ее работоспособности. Для ответа на вопрос: хорошо или плохо работает САР, важно знать, как она реагирует на управляющее воздействие, как сопротивляется действию возмущений, каков характер переходного процесса и т. д. Эти стороны САР объединяются в понятие качества регулирования.

Оценка качества САР является оценкой поведения системы при действии на нее того или иного воздействия. Для многих систем поддержания постоянства регулируемой величины типичны режимы, когда внешние воздействия изменяются скачкообразно или эти воздействия близки к скачкообразным. Примерами такого воздействия могут служить изменение нагрузки на двигатель в прокатных станах при входе штуки в валки клети, отключение или включение мощных электроприемников в электрических системах и т. д.

Т. к. условия работы САР при ступенчатом скачкообразном воздействии являются наиболее неблагоприятными, то качество процессов регулирования принято оценивать именно по отношению к ступенчатому воздействию.

Основными показателями качества при ступенчатом воздействии принято оценивать именно по отношению к ступенчатому воздействию.

Основными показателями качества при ступенчатом воздействии принято считать следующие:

1. Время регулирования или время переходного процесса

2. Перерегулирование – в статических системах или относительное отклонение – в астатических системах

3. Колебательность, т. е. число колебаний регулируемой величины за время переходного процесса.

Возможные графики изменений регулируемой величины САР можно изобразить так:

1. Монотонный процесс.

2. Колебательный процесс.

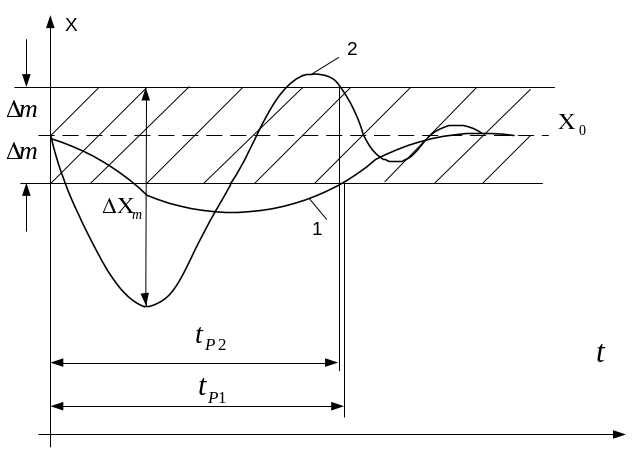
1. Первой важной качественной оценкой является время регулирования. В некоторых нелинейных и импульсных САР регулируемая величина может переходить от одного значения к другому за конечный промежуток времени. Но в линейных системах время регулирования теоретически равно ∞. Практически время регулирования можно определить лишь как время приближения к новому устойчивому состоянию с заданной точностью .

Временем регулирования называется наименьший промежуток времени, по истечению которого кривая переходного процесса регулируемой величины будет, при своем дальнейшем изменении, отклонятся от установившегося значения не более чем на .

Ширина зоны довольно существенно влияет на . Так для экспоненты при

, ;

при ,

обычно принимают .

2. Перерегулированием называется отношение разности между максимальным и устоявшимся отклонением регулируемой величины к ее установившемуся значению

, (2)

где – максимальное отклонение регулируемой величины;

– установившееся отклонение регулируемой величины.

Допустимое перерегулирование определяется конкретными условиями работы САР. Для систем регулирования скорости обычно допускают . Однако, это не догма.

Для тех переходных процессов, где начинаются и кончаются значения регулируемой величины одинаково, например, для астатических систем, понятие перерегулирования не теряет смысл. Оно заменяется понятием относительного максимального отклонения. Относительным максимальным отклонением называется отношение первого максимального отклонения регулируемой величины к заданному значению регулируемой величины.

3. Колебательность переходных процессов характеризуют часто числом колебаний регулируемой величины за время переходного процесса. Обычно принимают .