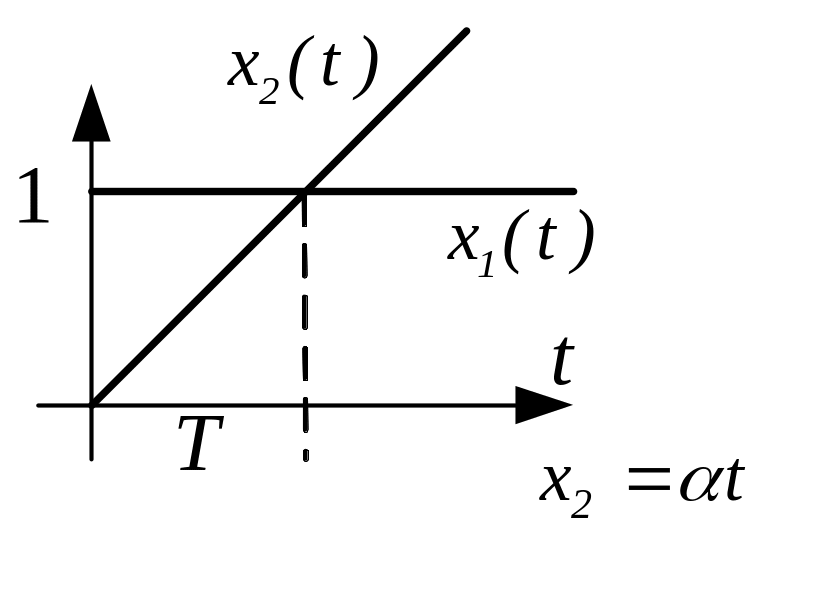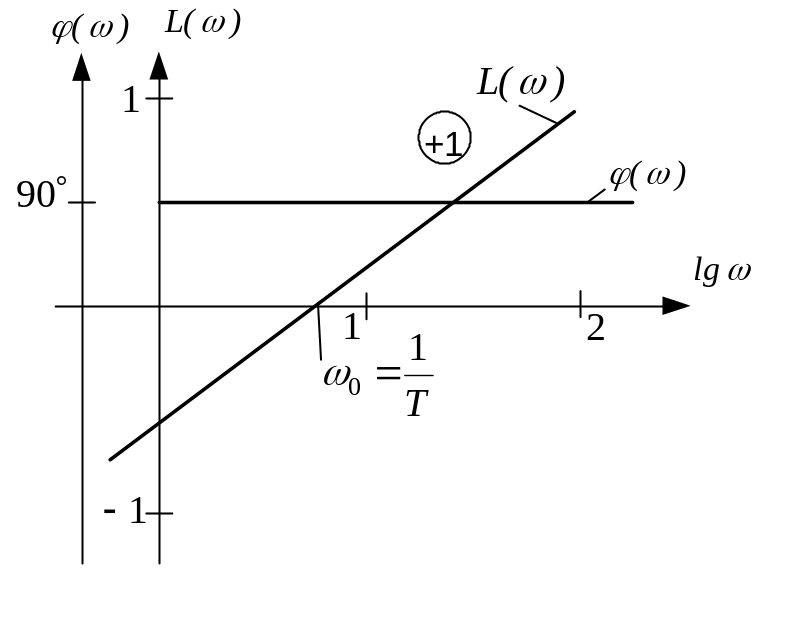1. Передаточная функция (1 стр 1)

Если на вход любой системы подать сигнал синусоидальной формы:

x_вх(t) = X_m cos(t) = X_m e ^jt .

Очевидно, что выходной сигнал будет иметь ту же форму:

x_вых(t) = Y_m cos(t+) = Y_m e ^{jt+)} .

Зависимость же между амплитудами и фазами выходного и входного сигналов определяет ДУ движения системы. Возмем произвольное, считая помеху f(t) равной нулю:

(T₂² p² + T₁ p + 1) x_вых(t) = (k₁ + k₂ p) x_вх(t) .

Подставим сигналы в уравнение движения:

T₂²(j)² X_вых e ^{jt+)} + T₁(j) X_вых e ^{jt+)} + X_вых e ^{jt+)} = k₁ X_вх e ^jt + k₂(j) X_вх e ^jt .

Найдем отношение выходного сигнала ко входному:

.

Вывод 1: Частотная передаточная функция получается из обычной заменой оператора Лапласа s на комплексную частоту j, т.е. в результате перехода от изображения Лапласа к изображению Фурье.

Вывод 2: ДУ движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывет изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.

Частотная передаточная функция может быть представлена в следующих видах:

W(j) = A() e ^j(),      или    W(j) = P() + jQ() ;

г де: W(j) – амплитудно-фазовая частотная характеристика (АФЧХ);

• A() - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя (АЧХ):

• () - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя (ФЧХ):

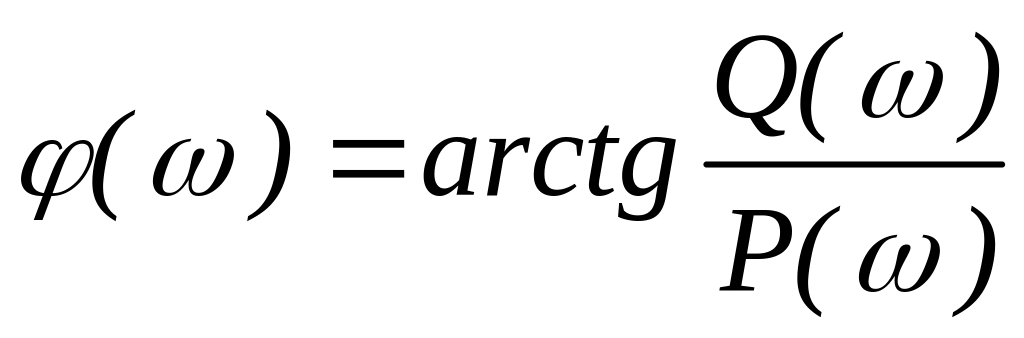
• P() и Q() - вещественная и мнимая части частотной ПФ. Для их нахождения необходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину. Логарифмические ЧХ - ЛАЧХ & ЛФЧХ Построение ЛАЧХ & ЛФЧХ производится по выражениям: L() = lg |W(j)| = lg A(),  [лог];    () = arg(W(j)),  [рад].

2. Математич. Описание идеальных звеньев. (2 стр. 2-3)

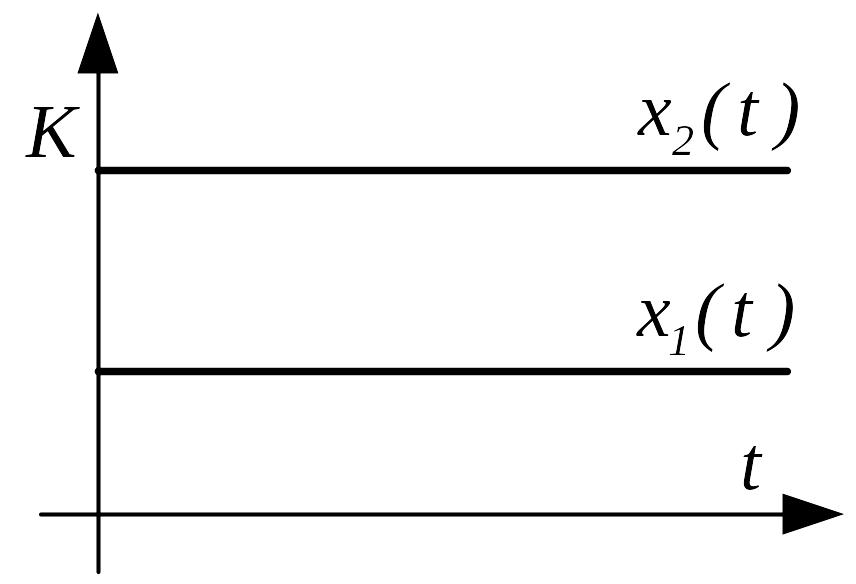
Безынерционное звено

	x2(t) = Kx1(t), в операторной форме X2(p) = KX1(p)
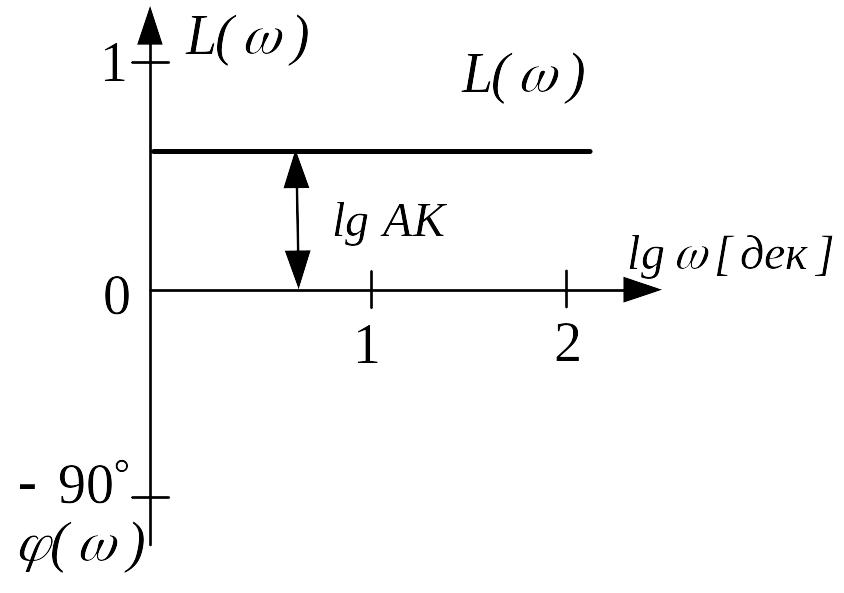
		Передаточная функция . Комплексный коэффициент передачи , то есть , . В логарифмическом масштабе . ЛАЧХ безинерционного звена представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на расстоянии . ЛФЧХ совпадает с осью абсцисс.

Интегрирующее звено

Идеальным интегрирующим звеном называется звено, выходная величина которого пропорциональна интегралу входной величины.

; ,

	; ; . , при , при , при ,
		То есть в логарифмическом масштабе ЛАЧХ – прямая линия. ЛАЧХ интегрирующего звена представляет собой прямую проходящую с наклоном и пересекающую ось абсцисс при частоте, равной обратной величине постоянной времени звена. ЛФЧХ представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на .

Дифференцирующее звено

Идеальным дифференцирующим звеном называется звено, выходная величина которого пропорциональна скорости изменения входной величины.

; ;

.

	; ; ; .
		при , ; при , ; при , .