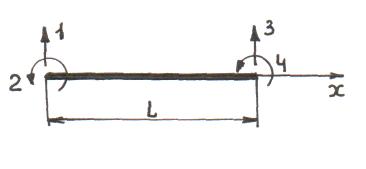
Колебания стержневых систем

Потенциальная и кинетическая энергия для элемента стержня с учетом поперечных и продольных сил инерции запишется в виде

(52)

(53)

где и – перемещения сечения элемента соответственно в продольном и поперечном направлениях;

m – погонная масса

Перемещения поперечных сечений и так же как и при статическом нагружении аппроксимируются по длине элемента функциями Эрминта. Но при колебаниях точные выражения функций Эрминта содержат сложные трансцендентные функции.

На практике оказывается удобным пользоваться функциями Эрминта как для статики, т.е. выражениями (29).

Тогда, согласно (39), (40) и (50)

, где

(54)

, где

После подстановки (54) в (52) и (53)

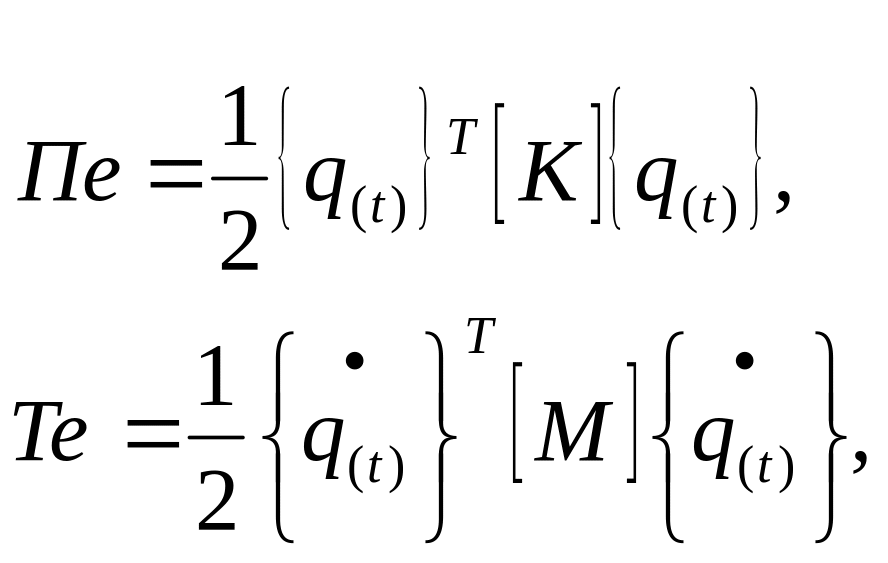
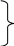(55)

Где [ K ] – матрица жесткости КЭ, определяемая выражением (42)

- матрица масс, причем первое слагаемое определяет матрицу масс при поперечных колебаниях, второе – при продольных колебаниях.

Развернутое выражение матрицы масс стержневого КЭ для анализа динамических задач с учетом поперечных и продольных колебаний для плоских рамных стержневых систем в местной системе координат примет вид

1/3	0	0	1/6	0	0
	13/35	11/210L	0	9/70	-13/420L
		1/105 L2	0	13/420L	-1/140 L2
			1/3
Симметр.				13/35	-11/210 L
					1/105 L2

В общей системе координат

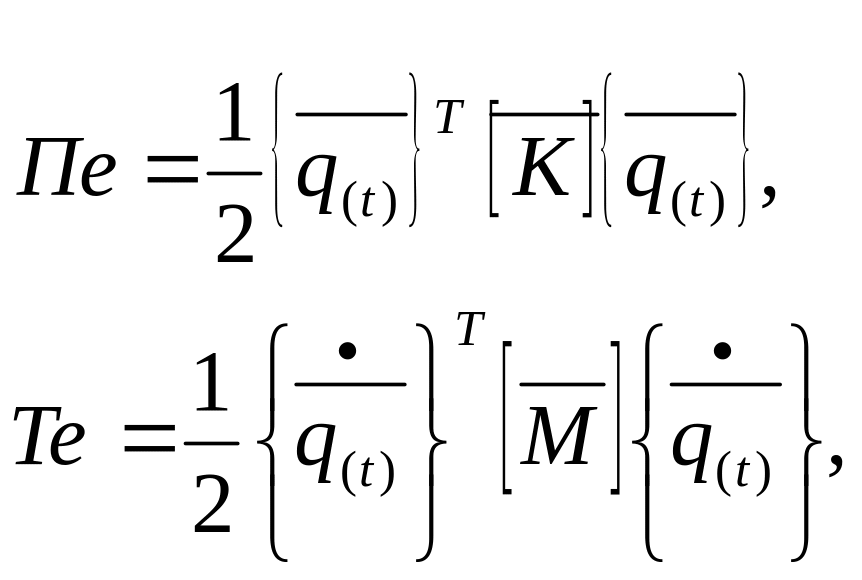} (56)

Где - м.ж. КЭ в общей системе координат (см. (47))

- матрица масс КЭ в общей системе координат.

(57)

Суммируя по всем элементам стержневой системы, получаем выражения для полной потенциальной и кинетической энергии

(58)

Подставляя П и Т в уравнения Лагранжа 2-го рода:

(59)

Получаем систему уравнений динамического равновесия рассматриваемой стержневой системы для определения вектора узловых перемещений

в общей системе координат при действии произвольных возмущающих узловых усилий

(60)

Где

К – глобальная матрица жесткости стержневой системы, составленная из матриц жесткостей КЭ.

М- глобальная матрица масс стержневой системы, составленная из матриц масс КЭ-ов и вычисляемая, например, по формуле, аналогичной формуле (20), т.е.

(61)

Где - квазидиагональная матрица,состоящая из матриц масс элементов, расположенных на главных диагональных блоках.

Физически уравнение (60)описывает условие динамического равновесия узлов рамы: сумма всех внешних усилий, приложенных в i-ом узле должна равняться сумме всех усилий и инерционных нагрузок от конечных элементов, сходящихся в этом узле. Исходя из этого условия можно сформулировать систему диф. уравнений (60).

При рассмотрении свободных колебаний (FREQUENCY) , т.е. возмущающие усилия равны нулю и конструкция совершает движение по гармоническому закону, т.е. , где q – вектор амплитуд узловых перемещений.

Тогда матричное уравнение (60) после сокращения на примет вид:

(62)

В результате пришли к задаче на собственные значения

, где (63)

Для определения частот свободных колебаний и соответствующих им форм колебаний q.

При рассмотрении вынужденных колебаний, вызванных внешними узловыми усилиями изменяющимися по гармоническому закону , (64)

Где

Р – вектор амплитуд внешних узловых усилий,

- круговая частота колебаний, т.е. число колебаний в 2П секунд;

f - число колебаний в единицу времени (Гц).

Тогда матричное уравнение (60) после сокращения на принимает вид

(65)

Здесь учтено, что при приложении возмущающих усилий с частотой , конструкция будет совершать гармонические колебания с той же частотой, т.е. .

системы линейных алгебраических уравнений относительно вектора амплитуд колебаний узлов q.

Устойчивость стержневых систем (BUCKLING)

Запишем выражение для потенциальной энергии деформации при изгибе призматического КЭ с учетом влияния осевой сжимающей силы T:

(66)

При отсутствии внешней нагрузки выражение упругой линии КЭ согласно (28) имеет вид через узловые перемещения

(67)

Или в матричном виде (68)

где - матрица-строка функций Эрмита, выражения которых в (29).

Внося (68) в (66) будем иметь

(69)

или (70)

где - матрица жесткости КЭ, элементы которой вычисляются через функции Эрмита как

, (i, j = 1, 2, 3, 4) (71)

Если мы выполним интегрирование по (71), то получим такую же матрицу жесткости, что и ранее получали (см. (13а) или 30).

Новым для нас здесь является матрица устойчивости КЭ

, (72)

элементы которой вычисляются через функции Эрмита как

(73)

Развернутое выражение матрицы устойчивости КЭ имеет вид

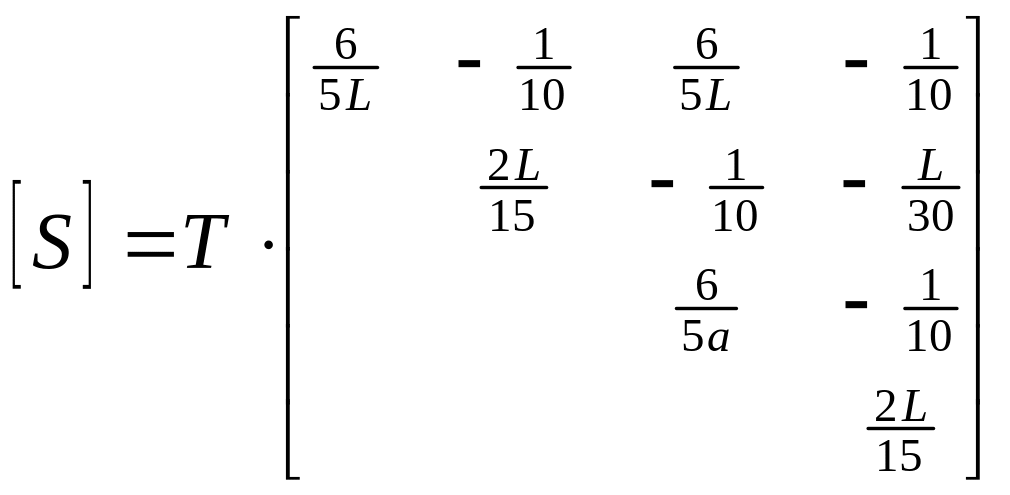(74)

Матрица симметричная.

В результате выражение для потенциальной энергии деформации КЭ принимает вид:

(75)

Или в общей системе координат:

, (76)

где

- м. > к. КЭ в общей (глобальной) системе координат;

- матрица устойчивости КЭ в общей системе координат.

Суммируя по всем КЭ стержневой системы, получаем выражение для полной потенциальной энергии деформации, минимизируя которую по вектору узловых перемещений всей конструкции (например, по (21) или (59)), получаем систему линейных алгебраических уравнений, описывающих равновесие узлов рамы.

, (77)

Где K – глобальная матрица жесткости;

S – глобальная матрица устойчивости, составленная из матриц устойчивости КЭ-ов и вычисляемая, например, по формуле, аналогичной формуле (20) или (61).

,

где - квазидиагональная матрица, состоящая из матриц устойчивости элементов.

Обычно внешние силы, действующие на раму, изменяются пропорционально одному параметру. Поэтому, если вместо сжимающей силы Т_е для е-го КЭ ввести величину

, (79)

где ,

t₀ – некоторая величина, имеющая размерность силы.

Тогда уравнению (77) можно придать вид:

(80)

В результате пришли к задаче на собственные значения

, где (81)

для определения критической нагрузки t₀ и соответствующих форм потери устойчивости.

Для рассмотренного треугольного элемента характерно то, что компоненты напряженного состояния оказываются постоянными в пределах КЭ, что видно из выражения (18), т. к. матрица [E] постоянна в пределах КЭ. Перемещения же по полю КЭ изменяются по линейному закону, что видно из (8).

Однако применение таких элементов даёт удовлетворительную прочность даже при весьма грубой конечно-элементной сетке. Точность вычислений зависит также от формы треугольного КЭ. Наилучшую точность дают равносторонние треугольные КЭ и наихудшую -остроконечные . Поэтому при создании конечно-элементной модели необходимо следить за её регулярностью.

Дальнейшее повышение точности расчетов с помощью плоских треугольных элементов требует задания линейного закона изменения компонентов напряжений в пределах элемента , т. е. использования для функций перемещений U_(x,y) и V_(x,y) полиномов 2-го порядка.

Треугольный плоский элемент с шестью узлами.

Кроме естественных трех узлов введены ещё три узла в серединах каждой из его сторон.

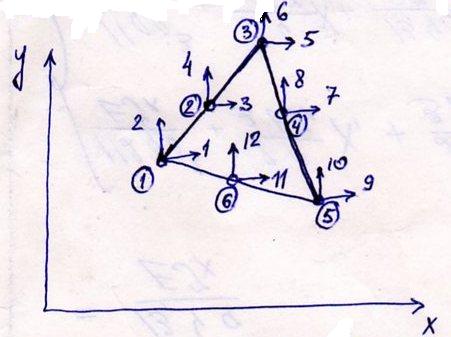
В этом случае возможно применение полного квадратичного полинома (т. к. 12 узловых перемещений ) для аппроксимации U_(x,y) и V_(x,y) :

(25)

Применение таких полиномов обеспечивает линейное изменение всех компонентов деформаций и напряжений в пределах элемента.

Подстановка в (25) значений узловых координат даёт:

{q} =[B]∙{α}_(12x12) (5)

Отсюда {α} =[B]^-1∙{α} (6)

Компоненты деформации из зависимостей Коши:

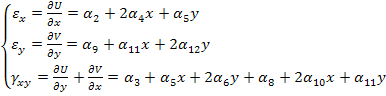(26)

или, в матричной форме,

{ }= [D_(x,y)]∙{α} (27)

0	1	0	2x	y	0	0	0	0	0	0	0	(28)
0	0	0	0	0	0	0	0	1	0	x	2y
0	0	1	0	X	2y	0	1	0	2x	y	0

Где

[D_(x,y)]=

Или { }=[D_(x,y)]∙[B]^-1{q}

По закону Гука (16)

{σ} =[E ]∙{ } =>{σ} =[E ]∙ [D_(x,y)]∙[B]^-1{q} (29)

Потенциальная энергия деформации КЭ

П_е = ,

где [K]_(12x12)= h∙[B^-1]^{T T}∙[E_𝜀]∙[D_(x,y)]∙dxdy∙[B]^-1 - (30)

-матрица жёсткости КЭ.

Найти конечные выражения для коэффициентов матрицы , как это сделано в (24), достаточно трудно, т.к. сама матрица [K] и матрица [B] имеют размер 12х12. Поэтому перемножение матриц удобнее производить в памяти ЭВМ при подсчете М.Ж. каждого К.Э., хотя это и увеличит затраты машинного времени.

Произвести перемножение ^T∙[E_𝜀]∙[D_(x,y)], интегрирование и получить выражения коэффициентов не составляет особого труда, т. к. она симметрична и содержит большое количество нулей.

Замечание: Выбор выражений, аппроксимирующих характер изменения перемещений или напряжений по объему К.Э. является одним из наиболее ответственных моментов в общей процедуре МКЭ. Всегда желательно, чтобы этот выбор приводил к удовлетворению уравнений равновесия и уравнений совместности деформаций внутри объёма конечного элемента, к отсутствию разрывов в компонентах перемещений и напряжений вдоль линии стыковки смежных элементов.

Ограниченность числа степеней свободы для конечного элемента не позволяет удовлетворить все эти условия, а следовательно, и получить точное решение задачи.

Надежным обоснованием в пользу выбора того или иного аппроксимирующего выражения является сравнение приближенного решения с точным, там где это возможно. (тестирование)

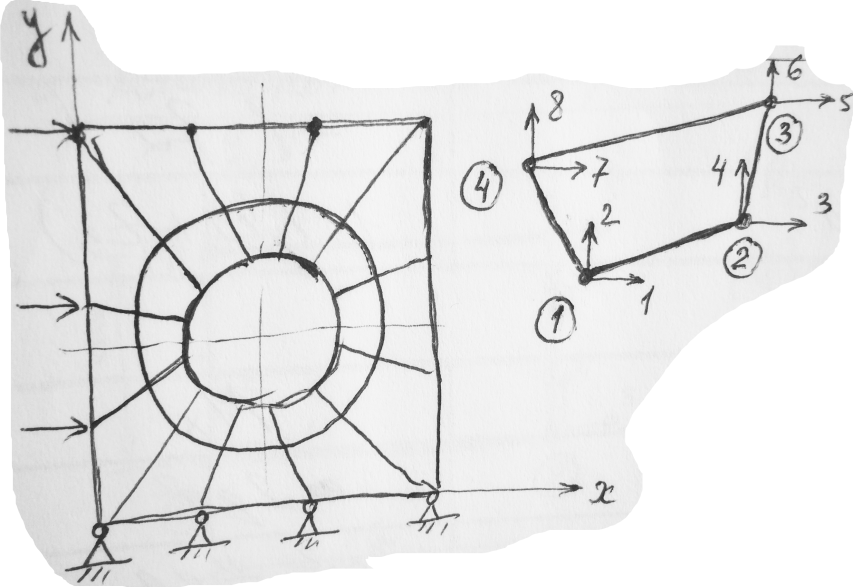
Четырехугольный элемент с линейным законом изменения

- узловые усилия;

- узловые

перемещения;

Элемент имеет 8 степеней свободы –

по две степени на каждый узел.

Так как три степени свободы КЭ связаны с перемещением его как абсолютно твердого тела, то оставшиеся пять степеней связаны с изменением его деформированного состояния, а следовательно и напряженного состояния. Поэтому вводим только 5 коэффициентов.

(31)

Или в матричной форме

(32)

1 у 0 0 0

где 0 0 1 х 0

0 0 0 0 1

Напряженное состояние элемента, выражаемое зависимостью (32), удовлетворяет уравнениям равновесия и условиям совместности деформаций внутри объема элемента.

Деформированное состояние внутри КЭ будет:

(33)

Интегрируя зависимости Коши

, , (34)

Из выражения (33) получим

(35)

Или в матричной форме

, (36)

где .

Здесь в результате интегрирования появились постоянные интегрирования , которые определяют перемещения КЭ как абсолютно твердого тела.

Взяв за основу аппроксимирующие выражения (35) и проводя рассуждения, аналогичные рассуждениям по формулам с (1) по (23) получим искомую матрицу жесткости элемента [K], т.е. подстановка координат узлов дает

(Закон Гука)

, где

- матрица жесткости

можно подсчитать вручную