4. Непрерывность функции комплексной переменной. Свойства непрерывных функций. Примеры.

Функция w = f(z), заданная на множестве S , называется непрерывной в точке z₀ S , если

= f (z₀), z S.

Иными словами , функция f (z) непрерывна в точке z₀, если для любого ɛ > 0 можно указать δ = δ(ɛ) > О такое, что для всех точек z S , удовлетворяющих условию |z – z₀| < δ, выполняется неравенство |f(z) - f(z₀)| < ɛ.

Для непрерывности функции комплексного переменного f(z) = u(x, у) + iυ(x, у) в точке z₀ = х₀ + iу₀ необходимо и достаточно, чтобы ее действительная и мнимая части – функции u(x,у) и υ(x,у) - были непрерывны в точке (х₀,y₀) по совокупности переменных х и у.

Это позволяет перенести на функции комплексного переменного основные свойства непрерывных функций двух действительных переменных: непрерывность суммы, произведения и частного двух функций, непрерывность сложной функции.

Если функция f(z) непрерывна в каждой точке множества S, то говорят, что функция f(z) непрерывна на множестве S.

T1. Если в комплексной функции выделить действительную и мнимую часть f(z)=u(x,y)+v(x,y).

f(z) непрерывна в z₀.

z₀=x₀+iy₀

Т2. Если f(z) непрерывна в замкнутой области D, ограничена, то и сама функция f(z) ограничена на D (граница входит).

Доказательство:

Предположим, что функция неограниченна. Найдется |f(z₁)|>1, найдется z₂ для которой |f(z₂)| >2.

{z_n} D.

Так как D ограничена, то {z_nк} z₀.

Тогда = .

W (противоречие).

Тогда наше предположение неверно.

Т3. f(z) на области D.

Действительная область =|f(z)| достигает своего наименьшего и наибольшего значения.

5. Равномерная непрерывность функции комплексной переменной. Свойства равномерно непрерывных функций. Примеры.

Опр: Пусть f(z) непрерывна в области D, если ( ɛ >0)( δ>0) ( z΄,z΄΄ ) |z΄-z΄΄|<δ => |f(z΄)-f(z΄΄)|<ɛ, то функция равномерно непрерывна.

Функция равномерно непрерывна в точке, если она непрерывна в точке.

Утв.: |z₁+z₂| |z₁|+|z₂| - обратное утверждение неверно.

П р.: А) f(z)=1/z

D: 0<|z|<1 – непрерывна, но не равномерно.

Б) f(z)=1/z

D⁰: 0<|z| r<1 – будет равномерно непрерывна.

Т. Всякая f(z) непрерывная в данной области, является непрерывной.

6. Последовательность функций комплексной переменной. Понятие сходимости и равномерной сходимости последовательности. Примеры.

f₁(z), f₂(z), … (27) – функциональная последовательность. При каждом фиксированном z, последовательность превращается в числовую.

Последовательность (27) сходится, следовательно для неё определена некоторая функция.

F: N C(z)

1 f₁(z)

2 f₂(z)

f(z)= .

Последовательность (27) называется сходящаяся, если существует предельная функция f(z).

Рассмотрим предельно широкая область определения.

Последовательность функций (27) по определению будет равномерно-сходящейся, если ( ɛ>0)( N)( z D)( >N) |f(z)-fn(z)|<ɛ.

{f_n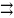(z)} f(z)

T. Если члены последовательности непрерывны в некоторой области D, а сама последовательность является равномерно сходящейся в некоторой области, то предельная функция также непрерывна. Весь аппарат вводится для рассмотрения комплексных рядов.