
- •Оглавление:
- •Введение
- •Часть I. Определение симедианы
- •1.1 Определения и их эквивалентность
- •1.2 Симедиана и антипараллельность
- •1.3 Симедиана и ортоизогональ
- •1.4 Симедиана и подобие
- •1.5 Симедиана и изогональное сопряжение
- •Часть II. Основная задача
- •2.1 Симедиана и инверсия
- •2.2 Основная задача и её применение
- •Часть III. Гармонический четырехугольник
- •3.1 Определение гармонического четырехугольника
- •3.2 Связь с симедианой (свойство)
- •3.3 Задачи
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •Заключение
- •Список литературы и web-ресурсов
3.3 Задачи
3.3.1
А) Пусть
четырехугольник
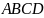 вписан в окружность .
Известно, что касательные к ,
проведенные в точках
и
,
пересекаются на прямой
или параллельны
.
Докажите, что касательные к ,
проведенные в точках
и
вписан в окружность .
Известно, что касательные к ,
проведенные в точках
и
,
пересекаются на прямой
или параллельны
.
Докажите, что касательные к ,
проведенные в точках
и
 пересекаются на прямой
пересекаются на прямой
 или параллельны
.
или параллельны
.
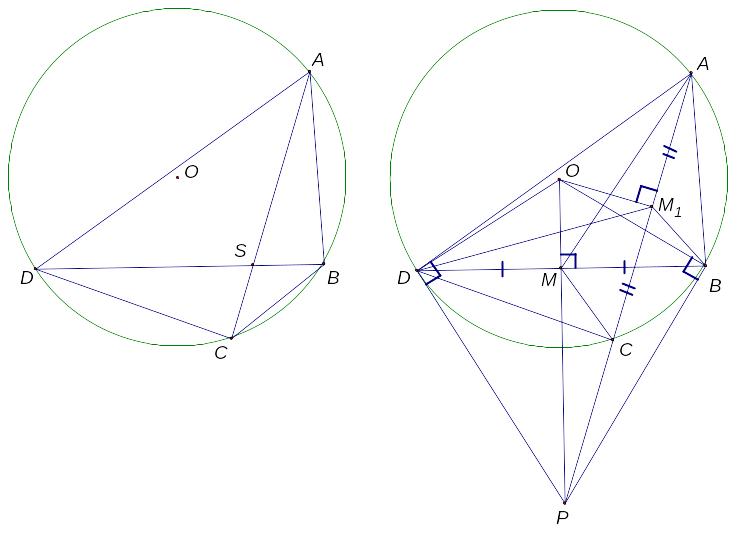
Рис. 1
Рис. 2
Доказательство:
Рассмотрим 2 случая:
1) Пусть касательные в точках и параллельны, то есть точки и диаметрально противоположны. Из этого следует, что, по условию задачи, касательные в точках и параллельны прямой . Таким образом, точки и симметричны относительно диаметра, поэтому прямая , являющаяся осью симметрии касательных в этих точках, пройдет через точку их пересечения. Что и требовалось.
2) Пусть касательные к окружности в точках и пересекаются в точке . Докажем, что – симедиана в треугольнике (см. основную задачу).
1 Способ:
Рассмотрим рис.1.
Заметим,
что
– симедиана в треугольниках
и
 .
Из второго определения симедианы
следует, что
.
Из второго определения симедианы
следует, что
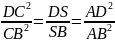 ,
то есть,
,
то есть,
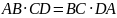 ,
следовательно, четырехугольник
– гармонический. Его диагонали является
симедианами (свойство
гармонического четырехугольника),
что и требовалось.
,
следовательно, четырехугольник
– гармонический. Его диагонали является
симедианами (свойство
гармонического четырехугольника),
что и требовалось.
2 Способ:
Рассмотрим рис. 2.
1)
Пусть
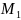 – середина отрезка
.
Проведем
– середина отрезка
.
Проведем
 и
и
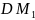 .
Достаточно доказать, что
.
Достаточно доказать, что
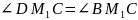 .
В таком случае
.
В таком случае
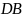 будет симедианой треугольника
(из задачи
№1.2.1).
будет симедианой треугольника
(из задачи
№1.2.1).
2)
Рассмотрим четырехугольник
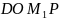 .
.
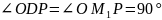 ,
следовательно,
– вписанный. Значит,
,
следовательно,
– вписанный. Значит,
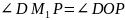 (они вписанные, опирающиеся на одну
дугу).
(они вписанные, опирающиеся на одну
дугу).
3)
Рассмотрим четырехугольник OM1BP.
∠OBP
= ∠OM1P
= 90 ,
следовательно, OM1BP
– вписанный. Значит, ∠BM1P
= ∠BOP
(они вписанные, опирающиеся на одну
дугу).
,
следовательно, OM1BP
– вписанный. Значит, ∠BM1P
= ∠BOP
(они вписанные, опирающиеся на одну
дугу).
4)
Заметим, что
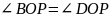 ,
так как
,
так как
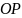 или
– медиана и биссектриса в равнобедренном
треугольнике
или
– медиана и биссектриса в равнобедренном
треугольнике
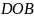 .
Следовательно,
.
Следовательно,
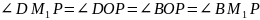 .
.
Таким образом, доказана следующая лемма: если у вписанного четырехугольника одна из диагоналей является симедианой, то он гармонический.
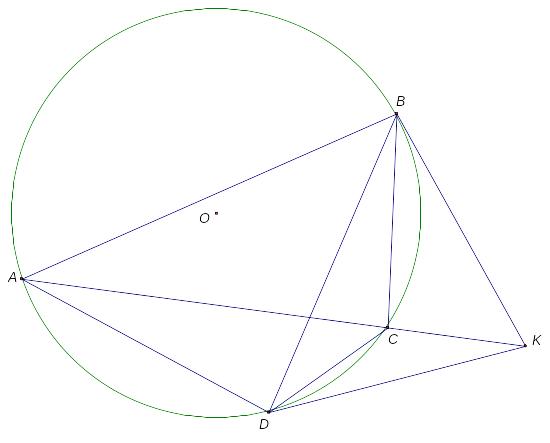
Б)
Касательная в точке
к описанной окружности
треугольника
пересекает прямую
в точке
.
Из точки
проведена вторая касательная
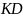 к окружности
.
Докажите, что
содержит симедиану треугольника
.
к окружности
.
Докажите, что
содержит симедиану треугольника
.
Доказательство:
В четырехугольнике , – симедиана треугольника (из основной задачи).
Таким образом, по лемме, – симедиана в треугольнике .
В) (Всероссийская олимпиада по геометрии 2008) Прямые, симметричные диагонали четырехугольника относительно биссектрис углов и , проходят через середину диагонали . Докажите, что прямые, симметричные диагонали относительно биссектрис углов и , проходят через середину диагонали .
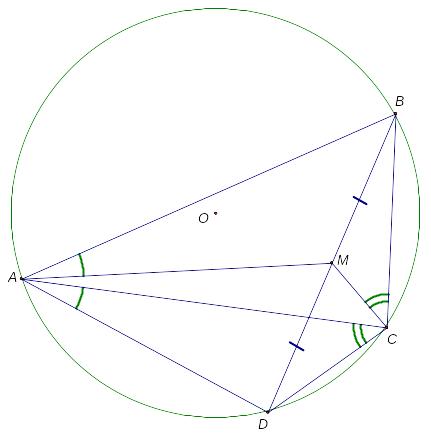
Доказательство:
Если
прямые
и
 ,
симметричные
относительно биссектрис углов, являются
медианами, значит
– симедиана в треугольниках
и
.
Таким образом, задача эквивалентна
предыдущей. Значит
–
симедиана в треугольниках
и
,
симметричные
относительно биссектрис углов, являются
медианами, значит
– симедиана в треугольниках
и
.
Таким образом, задача эквивалентна
предыдущей. Значит
–
симедиана в треугольниках
и
 ,
следовательно прямые, симметричные ей
относительно биссектрис углов, будут
содержать медианы в треугольниках
и
,
то есть будут пересекать
в середине.
,
следовательно прямые, симметричные ей
относительно биссектрис углов, будут
содержать медианы в треугольниках
и
,
то есть будут пересекать
в середине.
Г)
 – биссектриса угла
– биссектриса угла
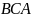 треугольника
.
–
симедиана треугольника
.
Точка
–
пересечение симедианы с описанной
окружностью. Докажите, что
треугольника
.
–
симедиана треугольника
.
Точка
–
пересечение симедианы с описанной
окружностью. Докажите, что
 –
биссектриса угла
–
биссектриса угла
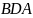 .
.
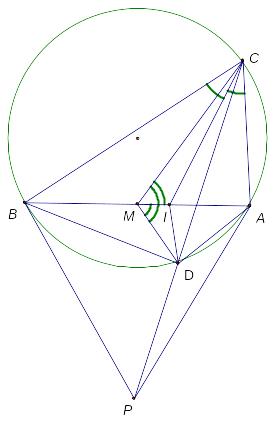
Доказательство:
