
Задание 1
.pdfЗадание 1
1Постановка задачи
Рассматривается одномерная задача о распространении звуковых волн (акустическое приближение) от гармонического источника на поверхно-
сти по неоднородной среде: |
|
8 |
|
p = c2(x)p |
xx |
>pttt=0 = 0 |
|
> |
|
> |
|
> |
|
> |
|
> |
|
< |
|
|
pt |
t=0 = 0 |
; |
|
|
|
|
|
p |
=0 = sin !t |
|
>ptx+ c(1)px |
x=1 = 0 |
||
> |
|
|
|
> |
|
||
> |
|
|
|
> |
|
|
|
> |
|
|
|
: |
|
|
|
где p(t; x) давление в момент времени t в точке x, ! циклическая частота, с которой воздействуют на поверхность, c(x) скорость звука в точке x.
2 Построение метода
Введем на отрезке [0; 1] сетку с шагом h = |
1 |
: |
|||
N |
|||||
|
|
|
|
||
|
|
|
|
|
|
xi = ih; i = 0; N |
|
|
|||
Приблизим p(t; x) кусочно-линейной на интервалах [xi; xi+1] функци-
ей:
|
N |
|
Xi |
p(t; x) = |
pi(t) i(x) |
|
=0 |
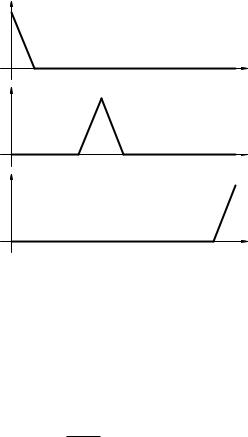
В качестве базисных функций |
i(x) возьмем функции, изображенные |
на рисунке 1. |
|
1
|
ψ0(x) |
|
1 |
|
|
x0 |
x1 |
xN−1 xN x |
|
ψI(x) |
|
1 |
|
|
x0 |
xI−1 xI xI+1 |
xN−1 xN x |
|
ψN (x) |
|
1 |
|
|
x0 |
|
xN−1 xN x |
Рис. 1: Базисные функции i(t; x)
Для таких функций i(xj) = ij, и, как следствие, коэффициенты pi(t) имеют смысл значений функции p(t; x) в точках x = xi.
Заметим, что p0(t) является известной, так как p0(t) = p(t; 0) = sin !t, поэтому неизвестными являются только p1(t); : : : ; pN (t).
Чтобы найти приближенное решение задачи, заменим строгое условие
1
c2(x)ptt pxx = 0
на более мягкое
G(p; w) Z0 |
1 |
c2(x)ptt pxx |
w(x)dx = 0 |
||
|
|
|
1 |
|
|
для всех w(x) из некоторого набора.
Заметим, что w(x) входит в функционал G(p; w) линейно, то есть если G(p; w1) = 0 и G(p; w2) = 0, то и G(p; w1 + w2) = 0. Следовательно, достаточно потребовать, чтобы функционал G(p; w) обращался в 0 не для всех w(x) из некоторого семейства функций, а только для функций w(x) из базиса в этом семействе.
Значение p в точке x = 0 зафиксировано. В этом смысле граничные условия называются жесткими. Напротив, граничное условие в точке x = 1 называется естественным. Это условие должно быть учтено в функционале G(p; w).
2
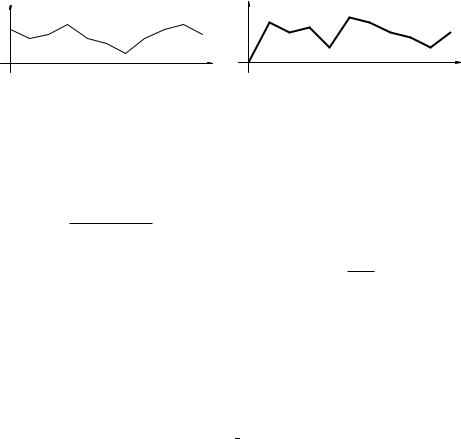
Для метода Галёркина семейство функций w(x) выбирается из того же класса, что и класс функций-решений, то есть кусочно-линейных непрерывных для данного случая. Жесткое граничное условие налагает на функцию w(x) дополнительное условие w(0) = 0. В некотором смысле, вместо требования выполнения уравнения в точке x = 0 мы требуем выполнение жесткого условия p(t; 0) = p0(t). Итого, все функции w(x)
представимы в виде w(x) = |
|
N |
|||||
|
j=1 wj j(x) (коэффициент при 0(x) равен |
||||||
0 |
|
j |
n |
базис в пространстве функций w(x), достаточно |
|||
). Поскольку f |
gj=1 |
||||||
|
|
|
P |
|
|||
потребовать G(p; |
|
j) = 0 для j = 1; : : : ; N. |
|||||
|
p(t, x) |
|
p0(t) |
|
|
x0 |
x1 |
xN−1 xN x |
|
W(X) |
|
X0 |
X1 |
XN−1 XN X |
Рис. 2: Кусочно-линейные функции p(t; x) и w(x)
Преобразуем выражение для G(p; w) = 0:
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
||
|
0 = G(p; w) = Z0 |
|
|
|
ptt pxx |
|||
= Z0 |
|
c2(x) |
||||||
1 p |
tt |
(t; x)w(x) |
|
|
1 |
|||
|
c2(x) |
dx px(t; x)w(x) 0 + |
||||||
w(x)dx =
Z 1
px(t; x)w0(x)dx
0
Учтем граничные условия w(0) = 0 и px(t; 1) = c(1)1 pt(t; 1):
1 p |
t; x)w(x) |
p |
(t; 1)w(1) |
|
1 |
||||
0 = G(p; w) = Z0 |
|
tt( |
dx + |
t |
|
|
|
+ Z0 |
px(t; x)w0(x)dx |
|
c2(x) |
|
|
c(1) |
|||||
Подставляя разложение для p(t; x) и |
j(x) вместо w(x), получаем си- |
||||||||
стему дифференциальных уравнений для pi(t):
NZ 1
Xi |
|
0 = p•i(t) |
|
=0 |
0 |
|
|
|
N |
||
i(x) j(x) |
dx + |
pi(t) |
i(1) j(1) |
+ |
|
|
|||
c2(x) |
Xi |
|||
=0 |
c(1) |
|||
|
|
|
|
|
NZ 1
Xi |
i0(x) j0 (x)dx; j = 1; : : : ; N |
(1) |
+ pi(t) |
||
=0 |
0 |
|
|
|
Для краткости введем несколько обозначений:
3
1 |
|
i(c2)(xj)( |
|
)dx |
|||||||
Матрица масс Mij = Z0 |
|
x |
|||||||||
|
|
|
|
x |
|
|
|
|
|
||
Матрица демпфирования Dij = |
|
|
i(1) j(1) |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
c(1) |
|||||||
Матрица жесткости Kij |
= Z0 |
1 |
i0(x) j0 (x)dx |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
(x) = |
|
|
|
|
|
|
|
|
|
|
|
c2(x) |
|
|
|
|
|
|
|
|
|
||
Отметим, что все матрицы оказались симметричными.
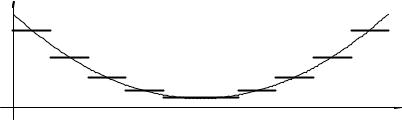
Для простоты вычисления матрицы M ограничимся случаем кусочнопостоянной функции c(x). Пусть значение c(x) на интервале [xi; xi+1] равно ci+1=2 (см. рис. 3).
|
C(X) |
|
|
|
C1/2 |
CN−1/2 |
|
|
C3/2 |
CN−3/2 |
|
|
|
C5/2 |
|
X0 |
X1 |
XN−1 |
XN X |
|
Рис. 3: Кусочно-постоянная функция c(x) |
|
|
Элементы матриц Mij; Dij и Kij равны нулю при ji jj > 1, поскольку подынтегральные выражения обращаются в нуль тождественно (носители функций i(x) и j(x) не пересекаются). Для остальных элементов
4

верны следующие выражения:
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1=2 h |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M00 = Z0 |
(x) 02(x)dx = 1=2 |
Z0 |
|
|
1 |
|
|
|
|
dx = h 1=2 Z0 |
(1 )2d = |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
h |
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
MNN = Z0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
h |
|
|
2 |
dx = h N 1=2 Z0 |
1 |
|
d = |
3 |
|
||||||||||||||||||||||||||||
(x) N (x)dx = N 1=2 Z1 h |
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + h |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
N 1=2 h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
Mii = Z0 1 (x) i2(x)dx = i 1=2 Zxixi1 |
x xi 1 |
2 dx + i+1=2 Zxixi+1 |
xi+1 x |
2 dx = |
|||||||||||||||||||||||||||||||||||||||||||||||
|
h |
h |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
1 |
+ |
|
1 |
)h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
i =2 |
|
i+ =2 |
|
; |
|
i = 1; : : : ; N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
M |
|
|
= M |
|
= |
|
1 (x) |
|
(x) |
|
|
(x)dx = |
|
1 |
|
xi+1 |
|
|
xi+1 |
|
x |
|
x xi |
|
|
|
dx = |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|||||||||||||||||||||||||||||||||||
|
i;i+1 |
|
|
|
i+1;i |
Z0 |
|
|
i |
|
|
j |
|
|
|
|
|
|
|
|
|
|
i+ =2 Zxi |
|
|
|
|
h |
|
|
|
|
|
|||||||||||||||||||
|
|
|
= i+1=2 h Z0 1 (1 )d = |
i+1=2 h |
; i = 0; : : : ; N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
0 1=22 |
2 1=2 |
+2 |
2 3=2 |
|
|
|
3=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 1= |
|
|
1= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||
M = h B |
|
|
|
3=2 |
|
|
|
2 3=2 + 2 5=2 |
|
|
|
|
|
|
|
|
5=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2 |
|
|
|
|
|
|
|
|
|
C |
|||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
N |
3 |
|
1 |
|
|
|
|
|
1 |
|
C |
||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
=2 |
|
|
|
|
|
=2 |
|
N =2 |
|
|
N =2 |
C |
||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
1 |
C |
|||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N =2 |
|
|
|
|
|
N =2 C |
|||||||||
|
|
|
@ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|||
Матрица демпфирования D содержит только один ненулевой эле-
мент:
1 DNN = c(1)
Ненулевые элементы матрицы K равны:
K00
KNN
Kii
Ki+1;i
|
1 |
|
|
|
|
|
h |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
= Z0 |
[ 00 (x)]2 dx = Z0 |
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
||||||||
h2 |
h |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
[ N0 (x)]2 dx = h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
xi+1 1 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||
= Z0 |
[ i0(x)]2 dx = Zxi 1 |
|
dx = |
|
; i = 1; : : : ; N |
1 |
|
|
|||||||||||||||
h2 |
h |
|
|
||||||||||||||||||||
= K |
|
|
= |
1 |
0(x) |
0 |
|
(x)dx = |
xi+1 |
1 |
dx = |
|
1 |
; i = 0; : : : ; N |
|
1 |
|||||||
|
|
Z0 |
|
|
h |
|
|||||||||||||||||
|
i;i+1 |
|
i |
i+1 |
|
|
|
|
Zxi h2 |
|
|
||||||||||||
5

0 |
1 |
11
|
|
B |
1 |
2 |
1 |
|
|
C |
K = |
1 |
|
1 |
.2 . |
1 . |
.. |
||
|
|
|||||||
|
h B |
|
|
.. .. |
C |
|||
|
|
B |
|
|
|
|
|
C |
|
|
B |
|
|
|
|
|
C |
|
|
B |
|
|
|
|
|
C |
|
|
B |
|
|
|
|
|
C |
|
|
B |
|
|
|
|
|
C |
@1 2 1A
1 1
В данных обозначениях система уравнений (1) записывается как:
N |
N |
N |
X |
X |
Xi |
p•i(t)Mij + |
pi(t)Dij + |
pi(t)Kij = 0; j = 1; : : : ; N |
i=0 |
i=0 |
=0 |
В этой системе только функции pi(t) при i > 0 являются неизвестными, в то время как p0(t) известна и ее следует исключить из системы уравнений:
N |
N |
N |
X |
X |
Xi |
p•i(t)Mij + |
pi(t)Dij + |
pi(t)Kij = fj(t); j = 1; : : : ; N; |
i=1 |
i=1 |
=1 |
где
fi(t) = M0;ip•0(t) D0;ip0(t) K0;ip0(t)
В таком виде систему можно записать в матричных обозначениях (используется тот факт, что все матрицы диагональны):
|
|
|
0 |
|
|
|
|
|
Mp•(t) + Dp(t) + Kp(t) = f(t) |
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||
h |
2 |
3=2 |
2 |
2 3=2 |
+22 5=2 |
|
|
|
|
5=2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||
|
|
|
B |
2 1= |
+ 2 3= |
|
3= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||||
M = |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
+ 2 |
|
|
|
|
|
|
|
||||||
6 |
|
|
|
|
|
|
|
2 |
1 |
|
|
N |
1 |
|||||||||||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
N =2 |
|
N =2 |
N =2 |
|
|
|
=2 |
C |
|||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
C |
||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N =2 |
|
|
|
|
|
N =2 C |
|||
|
|
|
@ |
|
1 0 1 2 1 |
|
|
|
|
1 |
|
0 |
0 |
|
|
|
|
|
1 |
|
A |
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K = |
|
B |
... ... ... |
|
|
C |
D = B |
|
|
|
... |
|
|
|
C |
|
|
|||||||||||||
h |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
B |
|
|
1 |
2 |
|
1C |
|
B |
|
|
|
0 |
|
|
|
C |
|
|
||||||
|
|
|
|
|
|
B |
|
|
|
|
|
C |
|
B |
|
|
|
|
|
1 |
|
C |
|
|
||||||
|
|
|
|
|
|
B |
|
|
|
|
1 |
1 |
C |
|
B |
|
|
|
|
|
|
|
C |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
B |
|
|
|
|
|
|
C |
|
B |
|
|
|
|
|
c(1) C |
|
|
|||||||
|
|
|
|
@ |
|
|
|
|
|
|
|
A |
|
@ |
|
|
|
|
|
|
|
A |
|
|
||||||
6

Здесь M; D и K подматрицы матриц M; D и K, но без нулевой строки и нулевого столбца, а p(t) вектор-столбец из функций p1(t); : : : ; pN (t). Вектор f(t) имеет вид
f(t) = |
M0;1 |
!2 sin !t + h sin !t 0 0 |
T |
||
|
|
|
1 |
|
|
Система (2) не разрешена относительно старшей производной p•(t), а вычислять обратную матрицу M 1 или решать линейную систему на каждом временном шаге иногда оказывается слишком трудоемко на практике. Вместо этого пытаются модифицировать метод так, чтобы матрица M получилась диагональной.
Простейший способ получить такой метод изменить процедуру вычисления элементов матриц M и K, заменив точное интегрирование на интегрирование методом трапеций (матрица K при этом не меняется):
Z xi+1 f(x)dx hf(xi) + f(xi+1)
xi 2
M00 = Z0 |
1 |
|
02(x)dx = h 1=2 Z0 |
1 |
|
|
|
|
|
1=2 h |
|||||||
|
(x) |
(1 )2d |
|||||||||||||||
|
2 |
|
|
|
|||||||||||||
f |
|
1 |
|
2 |
|
|
|
|
1 |
2 |
|
|
N 1=2 h |
||||
MNN = Z0 |
|
(x) |
N (x)dx = h N 1=2 Z0 |
|
d |
|
|
|
|
|
|||||||
|
2 |
|
|
|
|||||||||||||
f |
|
1 |
|
2 |
|
( i |
1=2 + i+1=2 )h |
|
|
|
|
||||||
Mii = Z0 |
|
(x) |
i (x)dx |
|
|
2 |
|
|
|
; i = 1; : : : ; N 1 |
|||||||
|
|
|
|
|
|||||||||||||
f |
= Mi+1;i = Z0 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
Mi;i+1 |
(x) |
i(x) |
j(x)dx = i+1=2 h Z0 |
(1 )d 0; i = 0; : : : ; N 1 |
|||||||||||||
f |
f1 |
|
|
|
|
0 |
T |
|
|
|
|
|
|
|
|
||
f(t) = h sin !t |
0 |
|
|
|
|
|
|
|
|
|
|
||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7

|
|
|
0 1=2 |
1=2 + 3=2 |
|
|
|
|
|
|
|
1 |
||||
M = |
h |
B |
|
|
3=2 + 5=2 . |
.. |
|
|
|
|
|
|
C |
|||
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
B |
|
|
|
|
|
|
|
|
|
C |
||||
f |
B |
|
|
|
|
|
|
|
|
|
|
C |
||||
B |
|
|
|
N |
3=2 |
+ N |
1=2 |
|
C |
|||||||
|
|
|
B |
|
|
|
|
|
|
|
|
N |
C |
|||
|
|
|
B |
|
|
|
|
|
|
|
|
1=2 C |
||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
C |
||
|
|
|
@ |
|
|
|
|
|
|
|
|
|
|
A |
||
|
|
|
|
h |
0 1=2 + 3=2 |
3=2 + 5=2 |
|
|
|
|
|
|
1 |
|||
M = |
|
|
B |
|
... |
|
|
|
|
|
|
C |
||||
|
2 |
|
N |
3=2 + N |
1=2 |
|
||||||||||
f |
|
|
|
B |
|
|
|
C |
||||||||
|
|
|
B |
|
|
|
|
|
|
|
N |
C |
||||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
1=2 C |
||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
@ |
|
|
|
|
|
|
|
|
A |
|
Ту же матрицу можно получить, просуммировав в каждой строке M элементы и поместив сумму на диагональ. Система обыкновенных дифференциальных уравнений теперь тривиально разрешается относительно старшей производной, поскольку матрица Mf диагональна.
Mfp•(t) + Dp(t) + Kp(t) = ef(t) |
(3) |
Дискретизируем временные производные стандартным образом:
Mpn+1 2pn + pn 1 |
+ Dpn+1 pn 1 |
+ Kpn = fn |
|
||
f |
|
|
|
e |
(4) |
2 |
|
2 |
|||
Здесь верхний индекс означает номер шага по времени. Перепишем разностную задачу в разрешенном относительно pn+1 виде:
M + |
|
M |
|
2K 2M pn = 2fn |
(5) |
|||
2 D pn+1 + |
2 D pn 1 + |
|||||||
f |
|
|
f |
|
|
f |
e |
|
В качестве начальных данных для (5) можно задать p0 = p1 = 0, что соответствует начальным данным для исходной задачи.
3Задание
Требуется запрограммировать метод (5) с параметрами ! = 5, числом интервалов N = 200, шагом по времени = h2 , и решить задачу до момента времени tmax = 10.
8
Скорость звука зависит от координаты по следующему закону:
ci+1=2 = c (i + 1=2)h ; c(x) = 0:1 + 3:6(x 0:5)2
В качестве решения требуется прислать график p(t; x) в момент времени t = tmax и исходный код программы.
9
